2. Работа по перемещению заряда в электрическом поле

2.1. Основные формулы и соотношения

Работа, совершаемая по перемещению заряда в электрическом поле, всегда равна убыли потенциальной энергии зарядов .

При перемещении заряда в электрическом поле работа внешних сил равна по модулю работе сил поля и противоположна ей по знаку:

.                                                            (2.1)

Работа, совершаемая электрическим полем при перемещении точечного заряда из одной точки поля, имеющей потенциал , в другую, имеющую потенциал ,

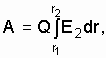  или                                                (2.2)

где – проекция вектора напряженности на направление перемещения; – перемещение для однородного поля.

Окончательно получим

                                                           (2.3)

где – угол между направлением вектора и перемещения .

2.2. Примеры решения задач

Задача 1. Электрическое поле создано двумя зарядами мкКл и мкКл, находящимися на расстоянии м друг от друга. Определить работу сил поля по перемещению заряда мКл из точки 1 в точку 2 (рис. 2.1).

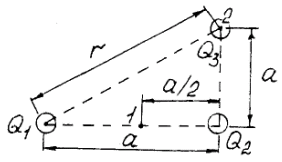
Рис.2.1

Решение. Для определения работы воспользуемся соотношением Применяя принцип суперпозиции электрических полей, определим потенциалы и точек 1 и 2 поля

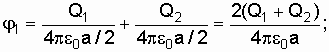
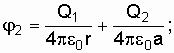
так как то .

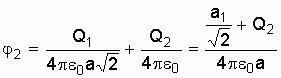Тогда работу определим из выражения

.

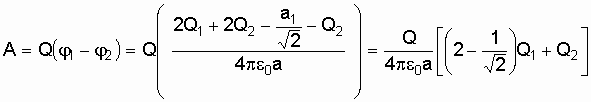Проверим размерность:

Произведем вычисления:

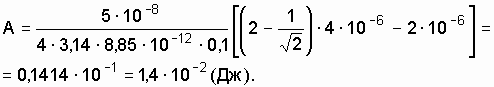
Задача 2. Определить ускоряющую разность потенциалов U, которую должен пройти в электрическом поле электрон, обладающий скоростью м/с, чтобы его скорость возросла вдвое.

Решение. Работа, совершаемая электрическим полем

.                                                              (2.4)

По закону сохранения энергии, эта работа равна изменению кинетической энергии электрона:

                                                 (2.5)

где – масса электрона, и – соответственно начальная и конечная скорости электрона. Приравнивая правые части равенств (2.4) и (2.5), получим

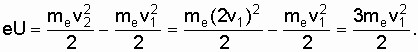
Отсюда искомая разность потенциалов

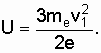
Проверим размерность

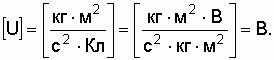
Произведем вычисления: .

2.3. Задачи

2.1. На отрезке прямого провода равномерно распределен заряд с линейной плотностью  1 мкКл/м. Определить работу сил поля по перемещению заряда нКл из точки В в точку С ( рис. 2.2). (Ответ: Дж).

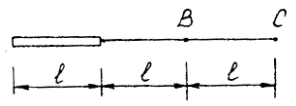
Рис.2.2

2.2. Тонкий стержень согнут в кольцо радиусом  см. Он заряжен с линейной плотностью нКл/м. Какую работу надо совершить, чтобы перенести заряд нКл из центра кольца в точку, расположенную на оси кольца на расстоянии см от его центра ? (Ответ: Дж).

2.3. Точечные заряды мкКл и мкКл находятся на расстоянии см друг от друга. Какую работу совершат силы поля, если второй заряд, отталкиваясь от первого, удалится от него на расстояние: а)  м; б) . (Ответ: a)  Дж; б) Дж).

2.4. Электрическое поле создано двумя одинаковыми положительными точечными зарядами Q. Найти работу сил поля по перемещению заряда нКл из точки 1 с потенциалом  В в точку 2 (рис. 2.3). (Ответ: Дж).

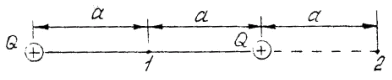
Рис. 2.3

2.5. Тонкий стержень согнут в полукольцо. Стержень заряжен с линейной плотностью нКл/м. Какую работу надо совершить, чтобы перенести заряд нКл из центра полукольца в бесконечность? (Вектор перемещения лежит в плоскости кольца). (Ответ: Дж).

2.6. Определить работу сил поля по перемещению заряда мкКл в поле, созданном заряженным шаром радиуса R, из точки, удаленной от первой на расстояние R, до точки, расположенной на расстоянии 2R. Потенциал шара равен кВ. (Ответ: Дж).

2.7. Бесконечная прямая нить несет равномерно распределенный заряд с линейной плотностью мкКл/м. Определить работу сил поля по перемещению заряда нКл из точки В в точку С (рис. 2.4). (Ответ: мкДж).

2.8. Какой минимальной скоростью должен обладать протон, чтобы достигнуть поверхности заряженного до потенциала В металлического шара (рис. 2.5)? (Ответ:  м/с).

Рис.2.4	Рис.2.5

2.9. Два точечных заряда нКл и нКл находятся на расстоянии см друг от друга. Какую работу необходимо совершить внешними силами, чтобы уменьшить вдвое расстояние между зарядами?(Ответ: Дж).

2.10. Диполь с электрическим моментом пКл м свободно установился в однородном электрическом поле напряженностью кВ/м. Определить работу внешних сил, которую необходимо совершить для поворота диполя на угол 180⁰ ? (Ответ:  Дж).

2.11. Закон зависимости напряженности электрического тока от расстояния имеет вид , где В/м и Вм². Определить работу сил поля по перемещению заряда Кл вдоль силовой линии из точки с координатой м в точку с координатой м. (Ответ: Дж).

2.12. Имеется плоский воздушный конденсатор, площадь обкладки которого равна м². Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от мм до мм, если при этом поддерживать неизменным заряд конденсатора Кл. (Ответ: Дж).

2.13. Имеется плоский воздушный конденсатор, площадь обкладки которого равна м². Какую работу необходимо совершить, чтобы медленно увеличить расстояние между обкладками от мм до мм, если при этом поддерживать неизменным напряжение на конденсаторе В. (Ответ:  Дж).

2.14. Пылинка массой 5 нт, несущая на себе электронов, прошла в вакууме ускоряющую разность потенциалов 1 мВ. Какую кинетическую энергию приобрела пылинка и какова ее скорость? (Ответ: Дж; м/с).

2.15. Ион атома лития прошел разность потенциалов  В, ион атома натрия ^ разность потенциалов  В. Найти отношение скоростей этих ионов. (Ответ: ).

2.16. При бомбардировке неподвижного ядра калия – частицей сила отталкивания между ними достигла Н. На какое расстояние приблизилась -частица к ядру? Какую скорость имела –частица вдали от ядра калия (влиянием электронной оболочки атома калия пренебречь)? (Ответ: м/с).

2.17. Электрон, обладающий кинетической энергией 10 эВ, влетел в однородное электрическое поле в направлении силовых линий. Какой скоростью будет обладать электрон, пройдя в этом поле разность потенциалов В? (Ответ: м/с).

2.18. Электрон, пройдя в плоском конденсаторе путь от одной пластины к другой, приобрел скорость 10⁵ м/с. Расстояние между пластинами 8 мм. Найти: 1) разность потенциалов между пластинами; 2) поверхностную плотность зарядов на обкладках. (Ответ: 1) В; 2) Кл/м²).

2.19. C поверхности бесконечного прямого цилиндра с радиусом основания Rс линейной плотностью 50 нКл/м вылетает -частица . В точке, удаленной на расстояние 8R от поверхности цилиндра, определить энергию -частицы. (Ответ: Е = 3,96 кэВ).

2.20. Электрон движется вдоль силовой линии однородного электрического поля. В некоторой точке поля с потенциалом  В электрон имел скорость м/с. Определить потенциал точки поля, дойдя до которой электрон потеряет половину своей скорости. (Ответ: В).

2.21. Вдоль силовой линии однородного электрического поля движется протон. В точке поля с потенциалом 600 В протон имел скорость 0,1 мм/с. Определить потенциал точки поля, в которой скорость протона возрастает в два раза. (Ответ: В).

2.22. В однородное электрическое поле напряженностью  кВ/м влетает вдоль силовой линии электрон со скоростью 1 мм/с. Определить расстояние, пройденное электроном до точки, в которой его скорость будет равна половине начальной. (Ответ: м).

2.23. Два бесконечных прямых проводника, заряженных с линейной плотностью нКл/м, находятся на расстоянии 2 см друг от друга. Какую работу на единицу длины нужно совершить, чтобы сблизить их на расстояние 5 мм. (Ответ: Дж/м).

2.24. Ионы лития и калия прошли одинаковую ускоряющую разность потенциалов. Найти отношение скорости этих потенциалов. (Ответ: 2,4 раза).

2.25. Какую работу нужно совершить, чтобы приблизить электрон из точки поля, удаленной от цилиндра на расстояние 20 см, к поверхности бесконечного прямого цилиндра радиусом  см, заряженного с линейной плотностью 100 нКл/м? (Ответ: Дж).

2.26. Две бесконечные равномерно заряженные плоскости с поверхностной плотностью зарядов  нКл/м²   и   нКл/м² расположены на расстоянии 20 см. Какую работу совершит поле при перемещении электрона от одной плоскости к другой? (Ответ: Дж).

2.27. Электрон и протон находятся на расстоянии 10 мм. Какая работа будет совершена при сближении зарядов на расстояние 5 мм ? (Ответ: Дж).

2.28. Заряженная бесконечная плоскость ( нКл/м²) и заряженный бесконечный прямой провод ( нКл/м), расположенный параллельно плоскости, находятся на расстоянии 4 см друг от друга. Определить работу электрического поля при перемещении заряда мкКл из точки поля А, удаленной от провода на расстояние см и от плоскости на расстояние см, в точку В, удаленную от провода на расстояние см и от плоскости – на  см. (Ответ: Дж).

2.29. См. условие задачи 2.28. Определить работу при перемещении заряда мкКл из точки поля А, удаленной от провода на расстояние см и от плоскости на расстояние см, в точку В, удаленную от провода на расстояние см и от плоскости – на см. Точки А и В расположены на одной прямой плоскости. (Ответ: Дж).

2.30. Электрическое поле создано точечным зарядом мкКл и прямым длинным проводом ( нКл/м), удаленными друг от друга на расстояние 5 см. Определить работу по перемещению заряда 1 нКл из точки А, равноудаленной от заряда Q и провода, в точку В, лежащую на прямой, перпендикулярной линии, соединяющей провод и заряд Q и отстоящей от провода на расстояние 4 cм. (Ответ: Дж).