1.2. Примеры решения задач

Задача 1. Четыре одинаковых положительных заряда по   расположены по вершинам квадрата. Какой отрицательный заряд нужно поместить в центре квадрата (рис. 1.1), чтобы система находилась в равновесии?

Решение. Все четыре заряда, расположенные по вершинам квадрата, находятся в одинаковых условиях, поэтому достаточно ограничиться рассмотрением одного из них (рис. 1.1).

На заряд , находящийся в вершине 4, действуют четыре силы, которые определяем по закону Кулона:

– две силы, создаваемые зарядами, находящимися в вершинах 1 и 2;

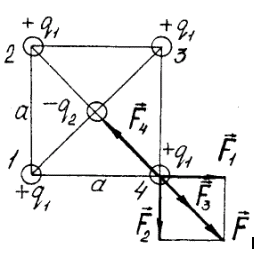
Рис. 1.1

;                                                  (1.25)

– сила, создаваемая зарядом, находящимся в вершине 3,

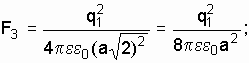                                       (1.26)

– сила, создаваемая зарядом ,

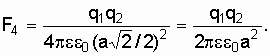                                       (1.27)

Для равновесия системы необходимо, чтобы геометрическая сумма этих сил была равна нулю, то есть . Векторы и направлены под углом 90⁰ друг к другу, поэтому их сумма представляет собой вектор, совпадающий по направлению с силой и численно равный

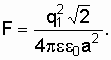                                                        (1.28)

Силы , и направлены по одной прямой, поэтому по абсолютному значению

 

или

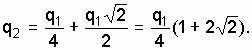
Подставив числовые значения, получим

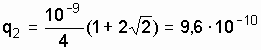Кл.

Задача 2. Между двумя разноименными плоскостями с поверхностной плотностью заряда Кл/м² подвешен заряженный резиновый шарик массой мг. Определить величину заряда на шарике, если он отклонился от положения равновесия на угол (рис. 1.2).

Решение. На шарик действуют две силы – сила тяжести шарика и электрическая сила поля двух разноименно заряженных плоскостей. Шарик будет находиться в равновесии, если равнодействующая этих сил уравновешивается реакцией нити. Следовательно, сила должна быть направлена вдоль нити, а для этого необходимо, чтобы

.                                                        (1.29)

Рис. 1.2

Сила численно равна произведению напряженности поля, создаваемого двумя параллельными разноименно заряженными плоскостями, на заряд шарика:

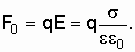                                                    (1.30)

Решая совместно уравнения (1.29) и (1.30), получим

Откуда

                                                       (1.31)

Проверим размерность искомой величины

Подставим числовые значения в формулу (1.31), получим

(Кл).

Задача 3. На пластинах плоского конденсатора находится заряд Кл, который создает поверхностную плотность заряда Кл/см², диэлектрическую проницаемость среды принять за единицу. Определить силу , с которой притягиваются пластины (рис. 1.3).

Рис. 1.3

Решение. Сила притяжения между пластинами возникает как сила электрического взаимодействия заряда и поля, в которое он внесен.

Заряд одной пластины конденсатора находится в поле, которое создает заряд другой пластины. Следовательно, , где – заряд, распределенный по поверхности первой пластины; – напряженность поля, созданная зарядом , находящимся на второй пластине.

Но ; Ф/м. Тогда расчетная формула примет вид

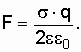
Проверим размерность:

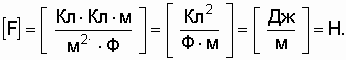
Произведем вычисления:

(Н).

Задача 4. Положительный заряд Кл равномерно распределен по тонкому проволочному кольцу радиуса см. Найти напряженность электрического поля на оси кольца в точке А, отстоящей от центра кольца на расстоянии см (рис. 1.4), диэлектрическую проницаемость среды принять за единицу.

Рис. 1.4

Решение. Разделим кольцо на одинаковые бесконечно малые участки . Заряд каждого участка можно принять за точечный. Напряженность электрического поля , создаваемая в точке А зарядом ,

                                                        (1.32)

Напряженность поля в точке А, которое создает заряженное кольцо, может быть найдена как векторная сумма напряженностей полей, создаваемых всеми точечными зарядами , то есть , где знак означает, что интегрирование (суммирование) векторов производится по всем элементам заряженного кольца .

Вектор можно разложить на две составляющие: , направленную вдоль оси кольца, и , направленную перпендикулярно к оси кольца: .

Следовательно, .

При определении напряженности следует учитывать только составляющие, направленные вдоль оси кольца, так как составляющие, направленные перпендикулярно оси, при сложении дадут нуль вследствие симметрии, то есть .

Составляющие для всех элементов кольца имеют одинаковые направления – вдоль оси. Таким образом,

.                                                        (1.33)

Подставим в выражение (1.33) формулу (1.32), получим

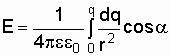.                                              (1.34)

Получим   (рис.1.4), тогда

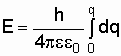
; Ф/м.

Проверим размерность:

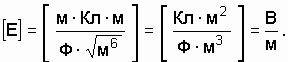
Произведем вычисления:

(В/м).

Задача 5. Два точечных электрических заряда  1 нКл и нКл находятся в воздухе на расстоянии см друг от друга. Определить напряженность поля, создаваемого этими зарядами в точке А, удаленной от заряда на расстояние см и от заряда – на см (рис.1.5).

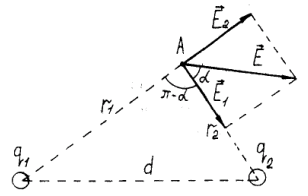
Рис. 1.5

Решение. Согласно принципу суперпозиции электрических полей, каждый заряд создает поле независимо от присутствия в пространстве других зарядов. Поэтому напряженность электрического поля в искомой точке может быть найдена как геометрическая сумма напряженностей и полей, создаваемых каждым зарядом в отдельности: .

Напряженности электрического поля, создаваемого в воздухе зарядами и ,

;                                                       (1.35)

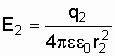.                                                      (1.36)

Вектор (рис. 1.5) направлен по силовой линии от заряда , так как этот заряд положителен; вектор направлен также по силовой линии, но к заряду , так как этот заряд отрицателен.

Модуль вектора найдем по теореме косинусов:

,                                                 (1.37)

где – угол между векторами и , который может быть найден из треугольника со сторонами , и ;

;       

.

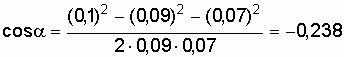Подставляя выражение Е₁ из формулы (1.35) и Е₂ из формулы (1.36) в формулу (1.37) и вынося общий множитель 1/4  ₀ за знак корня, получим:

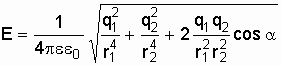; Ф/м.

Проверим размерность:

Произведем вычисления:

(В/м).