13. Электрический ток в газах

13.1. Основные формулы и соотношения

Подвижность ионов

,                                                                (13.1)

где – средняя скорость упорядоченного движения ионов; – напряженность электрического поля.

При небольших плотностях тока, текущего в газе, справедлив закон Ома:

,                                                        (13.2)

где – удельная проводимость газа; – заряд иона; – число ионов каждого знака (число пар ионов), находящихся в единице объема газа, ; и – подвижности ионов; Е – напряженность электрического поля.

При этом , где – число пар ионов, создаваемых ионизирующим агентом в единице объема за единицу времени, ; – коэффициент рекомбинации, м³/с.

Плотность тока насыщения в газе определяется формулой

,                                                           (13.3)

где – расстояние между электродами.

Для пробоя на оптических частотах требуются колоссальные поля в световой волне В/см, что соответствует интенсивности света порядка  МВт/см².

Среднеквадратичное поле в световой волне определяется по формуле:

,                                                  (13.4)

где – плотность потока энергии в фокусе; с – скорость света.

Диаметр кружка фокусировки определяется углом расходимости исходного светового луча и фокусным расстоянием линзы f

.

13.2. Примеры решения задач

Задача 1. Между пластинами конденсатора площадью  см² каждая находится водород объемом  см³. Концентрация ионов в газе равна  см^-3. Какое напряжение нужно приложить к пластинам, чтобы получить ток силой  мкА? Подвижность ионов: положительных   , отрицательных   .

Решение. Напряжение на пластинах конденсатора связано с напряженностью Е электрического поля и расстоянием между пластинами соотношением:

.                                                              (13.5)

Напряженность поля может быть найдена из выражения плотности тока . Отсюда .

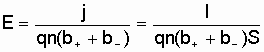Так как объем пространства, заключенного между пластинами, равен , то . Подставив выражения Е и в формулу (13.5), получим

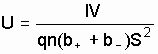.                                                  (13.6)

Произведя вычисления, найдем В.

Задача 2. Воздух в пространстве между пластинами плоского конденсатора с размерами  см ионизируется рентгеновскими лучами так, что в 1 см³ за 1 с образуется ионов и столько же свободных электронов. Пластины конденсатора соединены с источником напряжения  В через резистор с сопротивлением  Ом. Резистор с таким же сопротивлением  Ом включен параллельно конденсатору (рис.13.1).

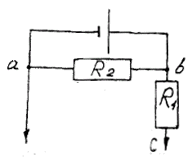
Рис. 13.1

Какой ток протекает через резистор ? Считать, что ионы и электроны достигают пластин конденсатора, не успев рекомбинировать, и что заряд каждого иона равен по модулю заряду одного электрона.

Решение. Ионы, возникающие под действием рентгеновских лучей внутри конденсатора, начинают двигаться к пластинам конденсатора под действием приложенного к нему напряжения. Ток через конденсатор , где – число ионов (или электронов), образующихся в единицу времени в единице объема конденсатора; – заряд иона; v – объем конденсатора.

Имеем . Кроме того, .

Из этих уравнений следует, что  (А).