9. Разветвление цепи. Правило кирхгофа
9.1. Основные формулы и соотношения
Разветвленная цепь – электрическая цепь, содержащая хотя бы один узел. Узел – это точка в электрической цепи, в которой сходятся не менее трех проводников.
Первое правило Кирхгофа. Алгебраическая сумма сил токов, сходящихся в узле, равна нулю:
.
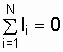(9.1)
Правило знаков: токи, идущие к узлу, считаются положительными, а исходящие из узла – отрицательными.
Второе
правило Кирхгофа.
Алгебраическая сумма падений напряжений
(то есть произведений
)
для любого замкнутого контура электрической
цепи равна алгебраической сумме ЭДС,
имеющихся в этом контуре,
.
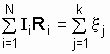(9.2)
Правила
знаков: если токи в замкнутом контуре
совпадают с выбранным направлением
обхода данного контура, то произведение
считается
положительным, в противном случае –
отрицательным. Если ЭДС повышает
потенциал в направлении обхода контура,
то есть, если при обходе приходится идти
от минуса к плюсу источника тока, то оно
считается положительным, в противном
случае – отрицательным.
Указания на расчет параметров разветвленной цепи при помощи правил Кирхгофа.
1. Обозначить стрелками предположительные направления токов, не задумываясь над тем, куда эти стрелки направить. Если в результате вычислений окажется, что ток положителен, то его направление выбрано правильно; в противном случае – ток течет в противоположном направлении.
2.
Если в разветвленной цепи имеется
токов,
то независимые уравнения типа (9.1) можно
составить лишь для
1
узлов; уравнение для последнего узла
будет следствием предыдущих.
3. Направление обхода для любого замкнутого контура выбирается произвольно (например, по часовой стрелке), все его участки следует обходить только в выбранном направлении. Если при решении уравнений получены отрицательные значения силы тока или сопротивления, то это означает, что ток через данные сопротивления в действительности течет в направлении, противоположном произвольно выбранному.
4. Число независимых уравнений, которые могут быть составлены по второму закону Кирхгофа [формула (9.2)], должно быть меньше числа замкнутых контуров в разветвленной цепи. Для составления уравнений первый контур выбирается произвольно. Все последующие контуры следует выбирать таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь цепи, не участвовавшая ни в одном из ранее использованных контуров. Число независимых уравнений типа (9.2) оказывается равным наименьшему числу разрывов, которые следует сделать в цепи, чтобы нарушить все контуры.
9.2. Примеры решения задач
Задача
1.
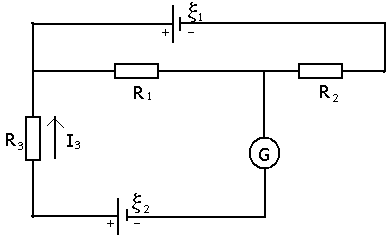
Электрическая цепь состоит из двух
гальванических элементов, трех
сопротивлений и гальванометра (рис. 9.1).
В этой цепи
Ом,
Ом,
,
В.
Гальванометр регистрирует силу тока I
=
мА,
идущего в направлении, указанном
стрелкой. Определить
,
I1
и I2.
Сопротивлением гальванометра и
внутренними сопротивлениями элементов
пренебречь.
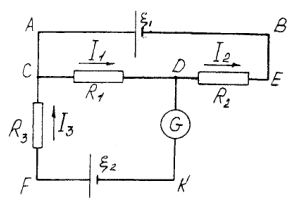
Решение. Выберем направление токов в цепи, как показано на рис. 9.2, и условимся обходить замкнутые контуры по часовой стрелке.
|
|
Рис. 9.1 |
Рис. 9.2 |
В цепи имеется два узла – С и D. По первому правилу Кирхгофа необходимо составить только одно независимое уравнение. Выберем узел D:
.
(9.3)
В разветвленной цепи имеется три замкнутых контура: АВЕDСА, СDKFC, ABEDKFCA, но наименьшее число разрывов, которые нужно сделать для нарушения всех контуров, равно двум. Следовательно, по второму правилу Кирхгофа нужно составить два независимых уравнения:
– для
контура АВЕDСА
или
;
(9.4)
– для контура СDKFC
.
(9.5)
Получим
систему, состоящую из трех уравнений с
тремя неизвестными
,
и
:
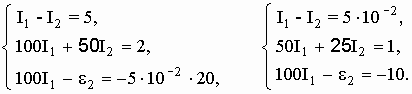
Для решения системы применим метод определителей:
;
;
;
.
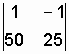
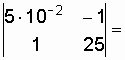
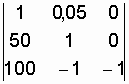
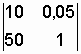
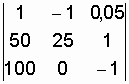
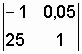
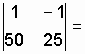
Определяем неизвестные величины:
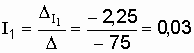(А);
(А);
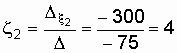(В);
Знак "–" для численного значения силы тока означает, что на рисунке выбрано направление тока , противоположное действительному.
Задача
2.
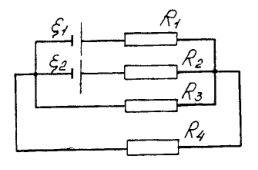
На рис. 9.3 представлена разветвленная
цепь с электродвижущими силами
В
и
В,
внутренние сопротивления источников
тока равны нулю. Определить силы токов,
текущих в сопротивлениях
и
,
если
Ом,
Ом.
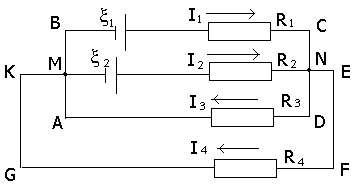
Решение: Выберем направление токов, как показано на рис.9.4; замкнутые контуры будем обходить по часовой стрелке.
|
|
Рис. 9.3 |
Рис. 9.4 |
В
цепи имеется два узла:
и
.
По первому правилу Кирхгофа надо
составить, следовательно, одно уравнение.
Выберем узел
:
.
(9.6)
Наименьшее число разрывов, которые нужно сделать для нарушения всех контуров, равно 3. Следовательно, по второму правилу Кирхгофа нужно составить три независящих уравнения:
– для контура MBCNM
;
(9.7)
– для контура АMNDA
;
(9.8)
– для контура GKMNEFG
.
(9.8)
Получили
систему из четырех уравнений с четырьмя
неизвестными
,
,
,
:
(9.9)
Подставляем
в уравнения известные значения параметров
цепи и решаем систему, используя метод
определителей. Так как необходимо по
условию задачи определить всего два
значения силы токов
и
,
то достаточно вычислить три определителя:
,
и
.
После подстановки известных величин в
систему (9.9) получаем:
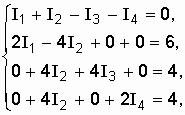
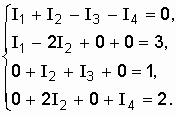
Находим необходимые определители системы.
;
;
.
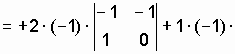
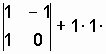
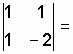
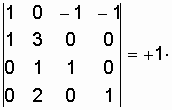
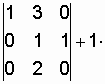
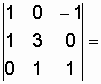
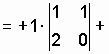
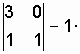
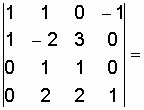
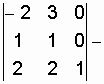
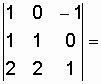
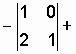
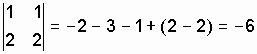Определяем значения сил токов и :
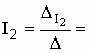
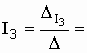
(А);
(А).