5.2. Примеры решения задач
Задача
1.
Определить электрическую емкость С
плоского конденсатора с двумя слоями
диэлектриков: фарфора толщиной
мм
и эбонита толщиной
мм,
если площадь
пластины
равна 100 см.
Решение.
Емкость
конденсатора по определению
где
–
заряд на пластинах конденсатора;
–
разность потенциалов между пластинами.
Но
.
Поэтому:
.
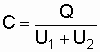(5.14)
Принять
во внимание, что
,
=
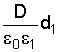и
=
.
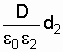Равенство (5.14) будет иметь вид:
,
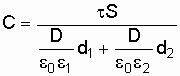(5.15)
где:
–
поверхностная плотность заряда на
пластинах;
и
–
напряженности поля в первом и втором
слоях диэлектрика соответственно;
–
электрическое смещение поля в диэлектриках.
Умножая
числитель и знаменатель равенства
(5.15) на
и
учитывая, что
,
окончательно получим
.
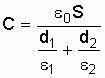Произведя вычисления по этой формуле, получим
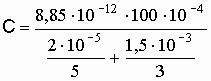
Ф
пФ.
Задача
2.
Плоский
воздушный конденсатор с площадью
пластины
равной 500 см2
подключен к источнику тока, ЭДС которого
равна 300 В. Определить работу А внешних
сил по раздвижению пластин от расстояния
1 см
до
см
в двух случаях: 1) пластины перед
раздвижением отключаются от источника
тока; 2) пластины в процессе раздвижения
остаются подключенными к нему.
Решение. 1–й случай. Систему двух заряженных и отключенных от источника тока пластин можно рассматривать как изолированную систему, по отношению к которой справедлив закон сохранения энергии. В этом случае работа внешних сил равна изменению энергии системы
,
(5.16)
где
–
энергия поля конденсатора в конечном
состоянии (пластины находятся на
расстоянии
);
–
энергия поля конденсатора в начальном
состоянии (пластины находятся на
расстоянии
).
Энергию в данном случае удобно выразить через заряд на пластинах, так как заряд пластин, отключенных от источника при их раздвижении, не изменится.
.
Получим
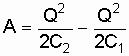или
.
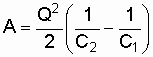Выразив
в этой формуле заряд через ЭДС источника
и начальную электроемкость
,
найдем
.
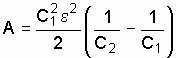(5.17)
Подставив
в формулу (5.17) выражения электроемкосте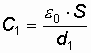й
и
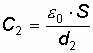плоского
конденсатора, получим
.
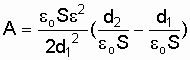(5.18)
Подставив числовые значения величин в формулу (5.18), получим
=
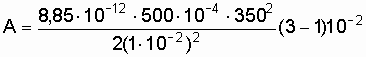3,98х10-6
(Дж) = 3,98 мкДж.
2–й случай. Пластины остаются подключенными к источнику тока, и система двух пластин уже не является изолированной (заряд с пластин при их раздвижении перемещается к клеммам батареи). Поэтому воспользоваться законом сохранения энергии в этом случае нельзя.
Следует заметить, что при раздвижении пластин конденсатора:
а)
разность потенциалов на них остается
неизменной
;
б)
емкость будет уменьшаться
.
Будут уменьшаться также заряд на
пластинах
и
напряженность электрического поля
.
Так как величины
и
,
необходимые для определения работы,
изменяются, то работу следует вычислять
путем интегрирования.
Запишем выражение для элементарной работы
,
(5.19)
где – напряженность поля, создаваемого зарядом одной пластины.
Напряженность поля , заряд и расстояние х взаимосвязаны так:
и
или
.
Подставив эти выражения и в равенство (5.19), получим
.
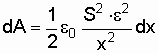Проинтегрировав это равенство в пределах от до , найдем выражение искомой работы
.
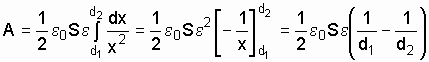Выполнив
вычисления по полученной формуле, найдем
1,33
мкДж.
Задача
3.
Металлический шар радиусом
см
несет заряд
нКл.
Шар окружен слоем парафина толщиной
см.
Определить энергию
электрического
поля, заключенного в слое этого
диэлектрика.
Решение. Так как поле, созданное шаром, является неоднородным, то энергия поля в слое диэлектрика распределена неравномерно. Однако объемная плотность энергии будет одинакова во всех точках, отстоящих на равных расстояниях от центра сферы, так как поле заряженного шара обладает сферической симметрией.
Энергия
в элементарном сферическом слое
диэлектрика будет иметь вид:
,
где
–
объемная плотность энергии;
–
элементарный сферический объем.
Полная энергия запишется выражением
,
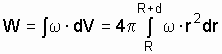(5.20)
где
–
радиус элементарного сферического
слоя;
–
его толщина.
Объемная
плотность энергии определяется по
формуле
где
–
напряженность поля. В нашем случае
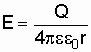и,
следовательно,
.
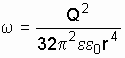Подставив это выражение плотности в
формулу (5.20), получим
.
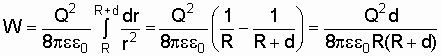Произведя
вычисления по этой формуле, получим:
мкДж.