Федеральное агентство по образованию
Государственное образовательное учреждение
высшего профессионального образования
«Тихоокеанский государственный университет»
Интегральное исчисление
Методические указания по дисциплине «Математический анализ»
для студентов дневной формы обучения
Хабаровск
Издательство ТОГУ
2007
УДК 22.17
Интегральное исчисление: методические указания по дисциплине «Математический анализ» для студентов дневной формы обучения / сост. Н.Б Лазарева, Н.Н.Ловцова – Хабаровск : Изд-во Тихоокеан. гос. ун-та, 2007. – 31с.
Методические указания составлены на кафедре прикладной математики информатики. В них изложены основные методы вычисления неопределённого интеграла, приложения определенного интеграла, рассмотрены примеры решения задач.
Печатается в соответствии с решениями кафедры «Прикладная математика и информатика» и методического совета факультета математического моделирования и процессов управления.
Тихоокеанский государственный
университет,2007
§ 1. Неопределённый интеграл
Функция F(x) называется первообразной для функции f(x), если
или
.
Всякая непрерывная функция f(x) имеет бесчисленное множество различных первообразных функций, которые отличаются друг от друга постоянным слагаемым.
Неопределённым
интегралом
от функции f(x)
называется совокупность всех её
первообразных:
.
Здесь
-знак
интеграла, f(x)
–подынтегральная функция, х –переменная
интегрирования.
Свойства неопределённого интеграла:
,
где
Если и
-любая дифференцируемая
функция, то
.
Если , то
,
и
.
Правильность результата интегрирования проверяется
дифференцированием
найденной первообразной, т.е.
.
Таблица основных интегралов представлена в приложении 1.
§ 2. Непосредственное интегрирование функций.
Задача нахождения неопределённых интегралов от многих функций решается методом сведения их к одному из табличных интегралов. Этого можно достичь путём алгебраических тождественных преобразований подынтегральной функции f(x) или подведения части её множителей под знак дифференциала.
Пример
1.
.
Пример
2.
Пример
3.
Пример
4.
=
§ 3. Интегрирование заменой переменной.
Если
функция
имеет непрерывную производную, то в
неопределённом
интеграле
можно перейти к новой переменной t
по формуле
,
затем найти интеграл и вернуться к исходной переменной х. Такой способ нахождения интеграла называется методом замены переменной или методом подстановки.
Пример
5.
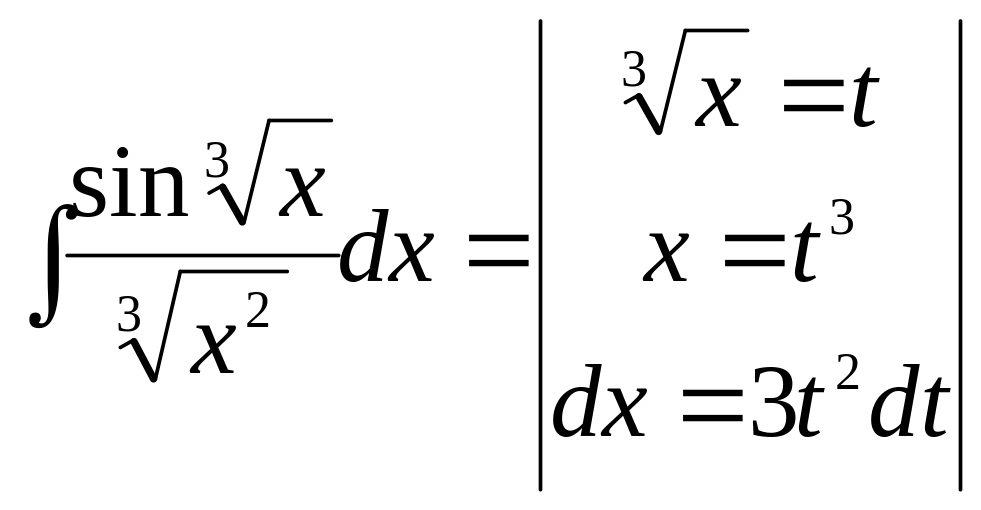
Пример
6.
Пример
7.
Пример
8.
