22. Теорема об изменении кинетической энергии системы. Теорема Кенига

Если связи таковы,что действительное перемещение находится среди возможных, то дифференциал кинетической энергии равен сумме элементарных работ активных сил на действительное перемещение.

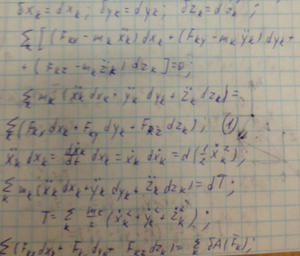dT=бA

Подставляя введенные обозначения в последнее выражение, получим математическую запись теоремы об изменении кинетической энергии системы материальных точек в интегральной форме:

T - T0 = Ae + Ai

(22)

то есть: изменение кинетической энергии системы при ее переходе из начального положение в текущее (или конечное) положение равно работе внешних и внутренних сил системы, совершенной при этом переходе.

Дифференцируя (22) по времени, учитывая, что кинетическая энергия системы в начальном положении - величина постоянная, имеем dT / dt = dA^e / dt + dAⁱ / dt. Откуда, зная что производная от работы является мощностью, получаем

dT / dt = Ne + Ni

(23)

Уравнение (23) представляет собой математическую запись теоремы об изменении кинетической энергии системы материальных точек в дифференциальной форме: производная по времени от кинетической энергии системы равна мощности внутренних и внешних сил системы.

Теорема Кенига

При выводе теоремы в интегральной форме мы определили кинетическую энергию системы как сумму кинетических энергий всех точек системы, то есть

(24)

где скорости точек системы определяются в инерциальной системе координат, которую принимают за неподвижную, и кинетическая энергия, следуя понятиям сложного движения, вычисляется в абсолютном движении.

Наиболее просто кинетическая энергия вычисляется, когда за подвижную систему координат (рис. 40) выбирают поступательно двигающуюся систему координат с началом в центре масс системы материальных точек (кенигова система координат). В этом случае абсолютное движение точки системы будет состоять из относительного движения в кениговой системе координат и переносного движения совместно с той же системой координат. По теореме о сложении скоростей Vⁱ = V_ie + V_ir. В силу того что кенигова система координат движется поступательно, переносные скорости всех точек системы одинаковы и равны скорости V_C ее центра масс, то есть V_ie = V_C, а абсолютная скорость точки системы равна V_i = V_C + V_ir. Учитывая, что _i² = V_i², подставляя выражение абсолютной скорости в (24), имеем

где выражение в скобках во втором слагаемом равно Q_r = MV_Cr, так как является количеством движения системы в подвижной кениговой системе координат. Но центр масс находится в начале кениговой системы координат и относительно ее не перемещается, то есть его относительная скорость V_Cr = 0. Поэтому второе слагаемое равно нулю и выражение кинетической энергии принимает вид

(25)

где T_Cr - кинетическая энергия относительного движении системы в кениговой системе координат, которую называют кинетической энергией движения системы относительно центра масс.

Уравнение (25) представляет собой математическую запись теоремы Кенига: кинетическая энергия системы материальных точек в ее абсолютном движении равна сумме кинетической энергии поступательного (переносного) движения системы вместе с центром масс, и кинетической энергии движения системы относительно центра масс.