Домашнє завдання

Обчислити інтеграли :

Заняття №3 Інтегрування підстановкою

Інтеграли від функцій, що містять квадратний тричлен.

І. Знайти слідуючи інтеграли :

ІІ. Інтеграли виду :

Для перетворень вказаних підінтегральних виразів до формул інтегрування треба із квадратного тричлена виділити повній квадрат, а потім підібрати відповідну формулу.

Приклади:

а)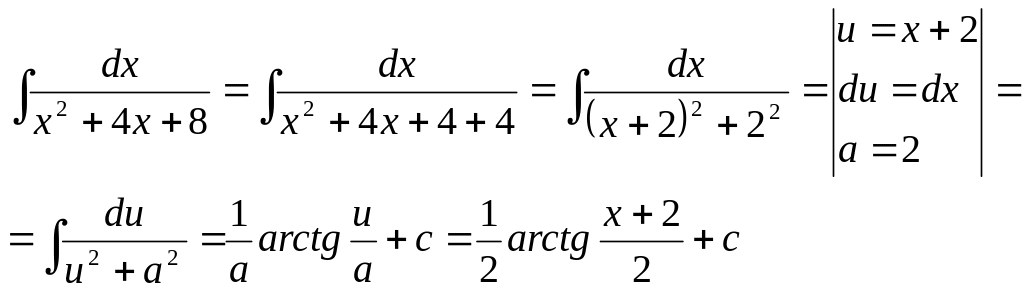

б)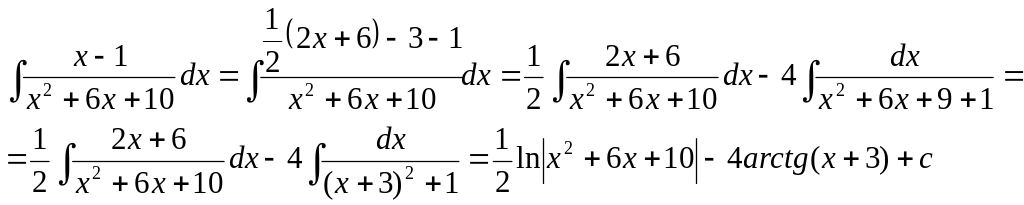

в)

г)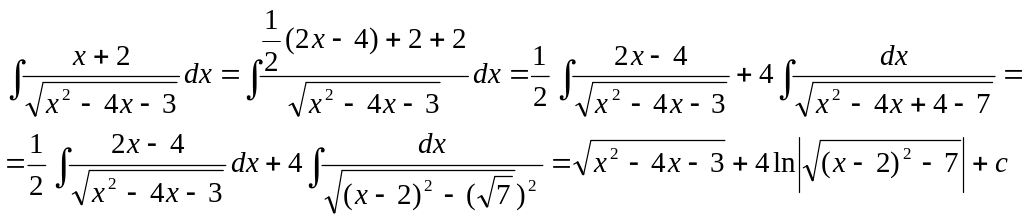

Обчислити інтеграли :

Домашнє завдання :

Обчислити інтеграли :

Заняття №4

Інтегрування частинами

Формула інтегрування частинами має вид

За допомогою цієї формули обчислення інтеграла зводиться до обчислення інтеграла , якщо останній буде простіший за вихідний.

Приклади :

1.

2.

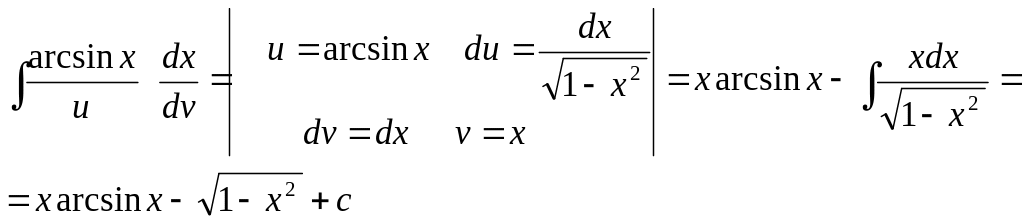
Формулу інтегрування частинами можна використовувати декілька разів.

Приклад:

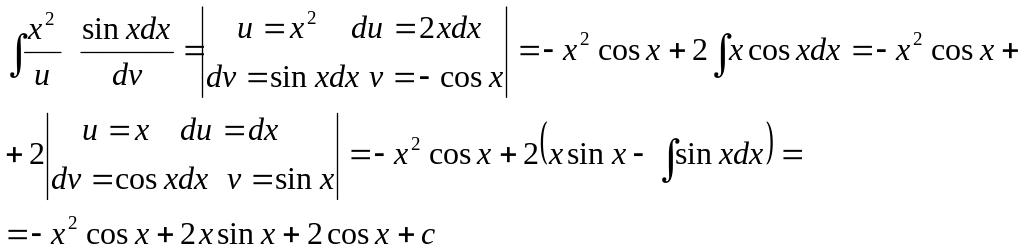
Обчислити інтеграли :

Домашнє завдання :

Заняття №5

Інтегрування раціональних дробів

Інтегрування раціонального дробу зводиться до інтегрування простіших дробів виду :

1) ; 2) ( n > 0 та ціле ) ; 3) ;

4) ( n > 0 та ціле ) .

Неправильну раціональну дріб, у якої степінь чисельника Р(х) вища чи дорівнює степені знаменника Q(x), можна діленням чисельника Р(х) на знаменник Q(x) за правилом ділення многочлена на могочлен, представити у виді суми многочлена М(х) та правильної остаточної дробі

.

Правильну раціональну дріб розкладають на елементарні, завжди інтегруємі складові дроби. Для чого знаходять корні рівняння Q(x)=0 і розкладають знаменник Q(x) на множники першої та другої степені.

Після чого правильну дріб розкладають на простіші за формулою

, де А₁ ,А₂ …,М₁ ,М₂… - невизначені коефіцієнти.

Розглянемо наступні види раціонального дробу:

Приклади:

а)

б)

в) (чисельник дорівнює похідній знаменника)

2.

Остаточно:

Приклади :

а) ;

б) ;

в) ;

г)

3.

Для визначення цього інтеграла поступають так :

а) у чисельнику дробу, яка стоїть під інтегралом, записують похідну знаменника, тобто (2х+р). Тотожними перетвореннями із 2х+р отримують заданий чисельник Ах+В, тобто 2х+р помножують на і до знайденого добутку добавляють ,тобто

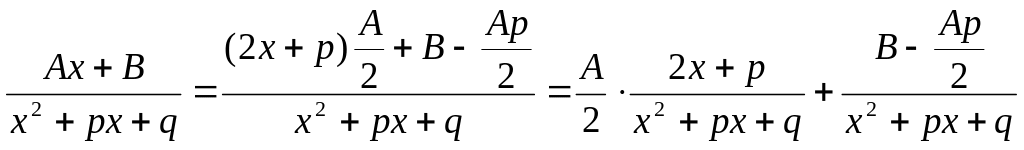
Перша дріб інтегрується просто: в чисельнику знаходять похідну знаменника – інтегрування зводиться до натурального логарифму модуля знаменника. Для інтегрування другої дробі у знаменнику виділяють повний квадрат

Інтеграл від другої дробі зводиться до табличного інтегралу :

або

Зауваження! коли в знаменнику дробі замість х² + рх + q знаходиться ax² + bc + c, то коефіцієнт а потрібно винести за дужки і тим самим звести цей випадок до попереднього.

Приклад :

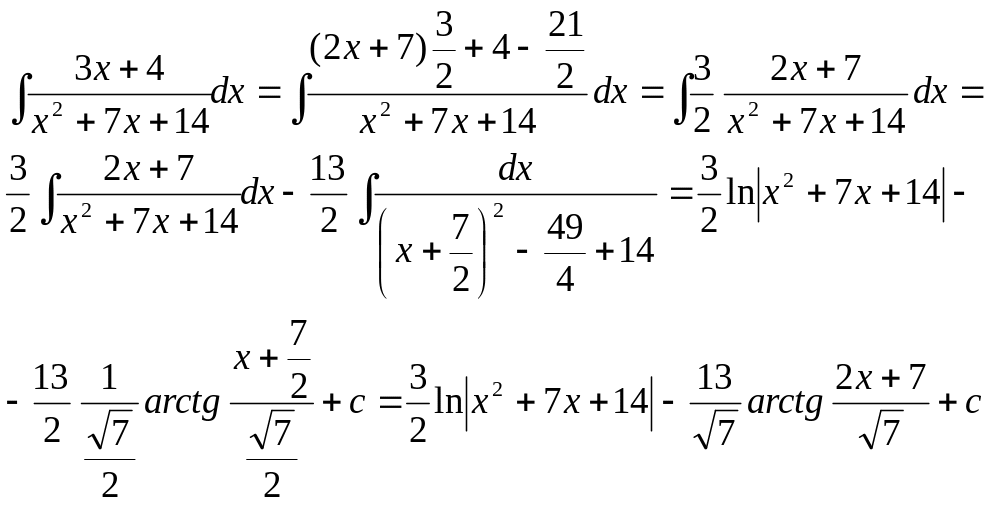
4.

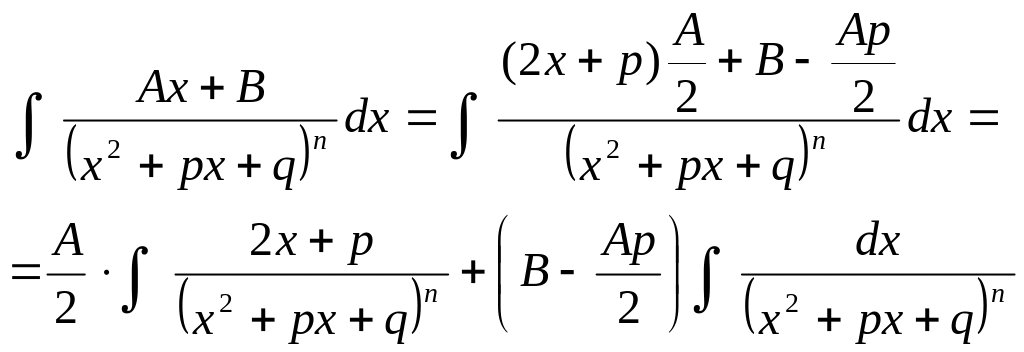
Інтеграл першого дробу обчислюється за формулою , друга дріб

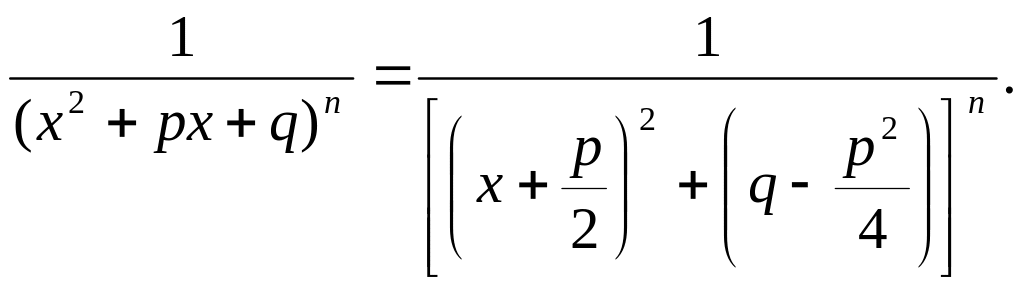
Приклад :

а)

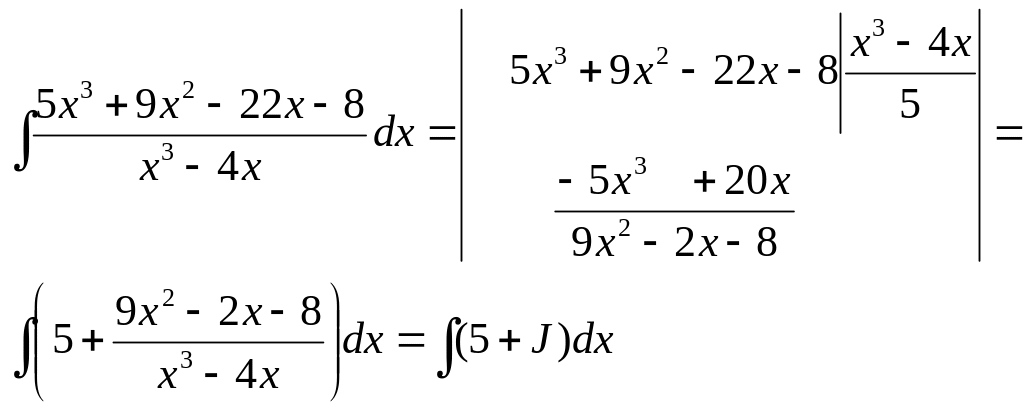
Застосуємо метод невизначених коефіцієнтів :

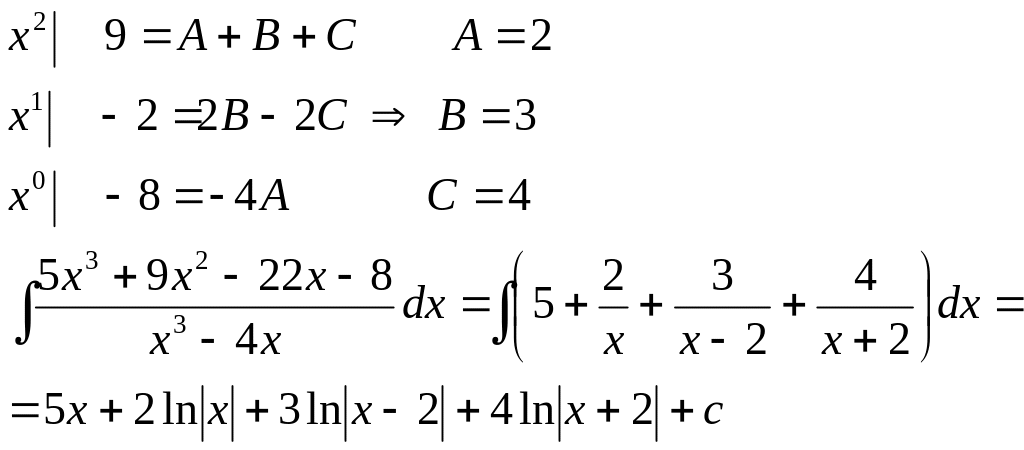
б)

в)

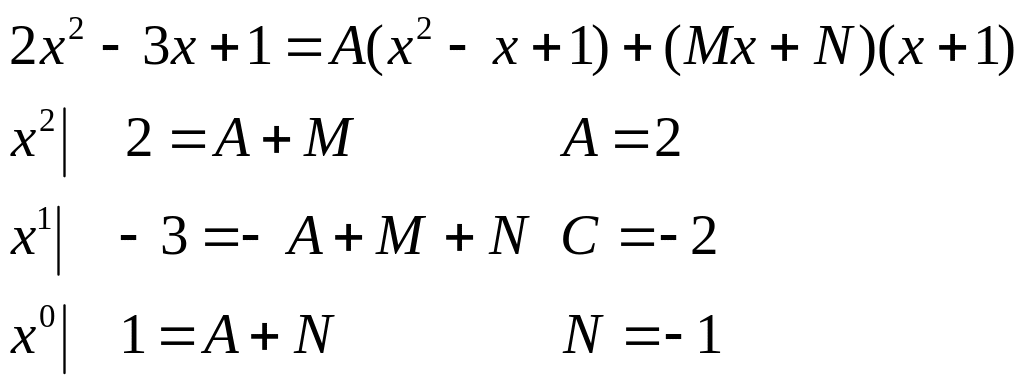
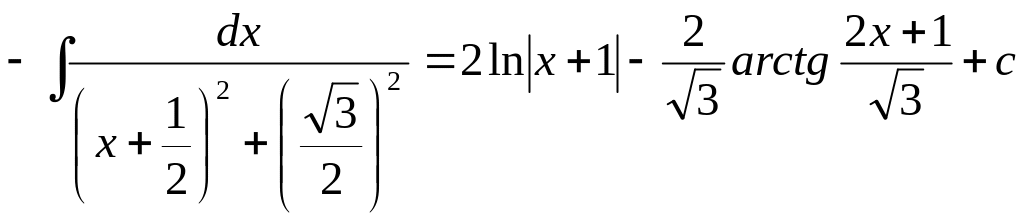
Обчислити інтеграли :

Домашнє завдання:

Обчислити інтеграли: