42 Вопрос. Свойства бесконечно малых функций.

Свойства бесконечно малых.  

1. Если функции альфа1(х) и альфа2(х) являются  бесконечно малыми, то функция альфа1(х)+альфа2(х) также есть бесконечно малая. Это свойство распространяется на случай  алгебраической суммы любого конечного числа бесконечно малых.  

2. Произведение ограниченной при х-->а  функции на бесконечно малую есть функция бесконечно малая.  

3. Произведение постоянной на бесконечно малую есть бесконечно малая.  

4. Произведение двух бесконечно малых есть бесконечно малая. Это свойство распространяется на любое  конечное число бесконечно малых.  

43 Вопрос. Сравнение бесконечно малых и бесконечно больших функций.

Пусть альфа(х) и бета(х) две функции заданные для одних и тех же значений аргумента и обе являются бесконечно малыми в точке х=а.

4. Говорят, что альфа(х) является в точке а бесконечно малой более высокого порядка, чем бета(х), если

5. Говорят, что альфа(х) и бета(х) являются бесконечно малыми одного порядка в точке а, если , где А — конечное число отличное от нуля.

6. Говорят, что альфа(х) и бета(х) являются в точке а эквивалентными бесконечно малыми, если В этом случае пишут

Для обозначения того, что альфа(х) является в точке а бесконечно малой более высокого порядка чем бета(х)используют следующую запись .

Теорема Если функции альфа(х) ~ альфа1(х), x=a, бета(x)~бета1(x), x=a и существует предел , а также и они равны

Доказательство: Действительно

44 Вопрос. Дифференцирование суммы, разности, произведения и частного двух функций.

Теорема. Пусть функции и определены в окрестности точки и дифференцируемы в этой точке. Тогда в этой точке дифференцируема и каждая из функций:

, , и (при ),

причем

,

(1)

,

(2)

,

(3)

.

(4)

Д о к а з а т е л ь с т в о: 1. Дифференцируемость функции и равенство (1) очевидно будут установлены, если будут установлены дифференцируемость функции и равенство (3). В последнем случае достаточно будет рассмотреть функцию .

2. Дифференцируемость функции и равенство (2) вытекают из того, что имеют место равенства

и из того, что по условию существуют конечные пределы

и ,

при этом следует помнить, что дифференцируемость функции в точке равносильна существованию конечной ее производной в этой точке.

3. Дифференцируемость произведения функций и равенство (3).

Пусть

.

Тогда

,

и, следовательно,

.

(5)

В силу дифференцируемости функций и в точке , существуют конечные пределы

, и

(6)

Поэтому из (5) следует, что существует конечный предел

,

(7)

т.е. функция дифференцируема в точке . Переходя в равенстве (5) к пределу при с учетом равенств (6) и (7) получим равенство (3).

4. Дифференцируемость и равенство (4). Положим . По крайней мере, в некоторой окрестности точки , это определение корректно, так как и функция непрерывна в точке .

Далее, имеем:

,

и, следовательно,

.

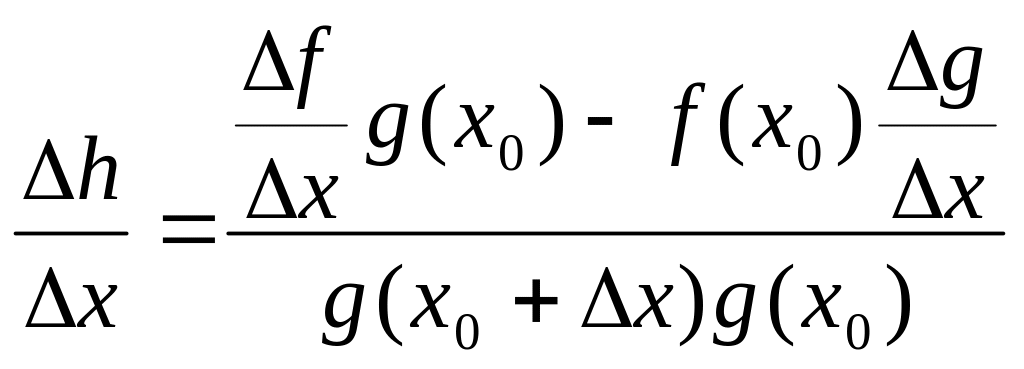Рассуждая теперь аналогично пункту 3 данного доказательства, убеждаемся, что функция дифференцируема в точке , а переходя здесь к пределу при получим также и равенство (4).