11. Оценка погрешностей средств измерений.

Погрешности средств измерений, отклонения метрологических свойств или параметров средств измерений от номинальных, влияющие на погрешности результатов измерений, получаемых при помощи этих средств. Составляющие этих погрешностей, зависящие от Погрешности средств измерений, называются инструментальными погрешностями (инструментальными ошибками). Погрешности средств измеренийвыражают в форме абсолютных, относительных или приведённых погрешностей (т. е. соответственно в единицах измеряемой величины, в долях или процентах от неё либо в процентах от верхнего предела измерений, диапазона измерений или длины шкалы).

Погрешности средств измерений, имеющие место при нормальных условиях применения средств измерений, называют основными; погрешности, вызванные отклонением значений влияющих величин (температуры, частоты электрического тока и т.п.) от принятых за нормальные, — дополнительными. Для каждого типа средств измерений устанавливаются пределы допускаемых погрешностей, определяющие классы точностисредств измерений. При измерениях постоянных величин, когда используются установившиеся показания средств измерений, на результаты влияют только статические Погрешности средств измерений При измерениях изменяющихся величин к статическим добавляются динамическиеПогрешности средств измерений и общая погрешность возрастает.

По своему характеру Погрешности средств измерений бывают систематические, т. е. сохраняющиеся постоянными или закономерно изменяющиеся, и случайные, т. е. изменяющиеся случайным образом. Так, неправильно нанесённые отметки на шкале прибора или неточная подгонка мер (например, гирь) вызывают систематические погрешности; трение подвижных частей прибора — случайные. СистематическиеПогрешности средств измерений можно исключать введением поправок или умножением показаний на поправочные множители.

12. Свойства оценок случайных погрешностей: несмещенность, эффективность, состоятельность. Точечные и интервальные оценки.

Рассмотрим оценку θ_n числового параметра θ, определенную при n = 1, 2, … Оценка θ_n называется состоятельной, если она сходится по вероятности к значению оцениваемого параметра θ при безграничном возрастании объема выборки. Выразим сказанное более подробно. Статистика θ_n является состоятельной оценкой параметра θ тогда и только тогда, когда для любого положительного числа ε справедливо предельное соотношение

При разработке новых методов оценивания следует в первую очередь проверять состоятельность предлагаемых методов.

Второе важное свойство оценок – несмещенность. Несмещенная оценка θ_n – это оценка параметра θ, математическое ожидание которой равно значению оцениваемого параметра: М(θ_n) = θ.

Эффективная оценка – это несмещенная оценка, имеющая наименьшую дисперсию из всех возможных несмещенных оценок данного параметра.

Понятие эффективности вводится для несмещенных оценок, для которых М(θ_n) = θ для всех возможных значений параметра θ. Если не требовать несмещенности, то можно указать оценки, при некоторых θ имеющие меньшую дисперсию и средний квадрат ошибки, чем эффективные.

Точечные и интервальные оценки погрешности

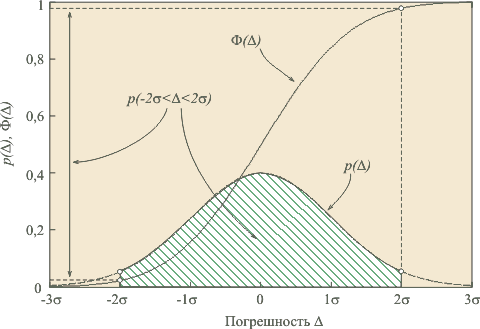
Рис. 4.3. Иллюстрация понятий доверительного интервала и доверительной вероятности

Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкам относится математическое ожидание погрешности и среднеквадратическое отклонение. В качестве интервальной оценки используют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью  . Эта вероятность называется доверительной или надежностью оценки погрешности.

Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.

Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.

Смысл интервальной оценки погрешности иллюстрируется рис. 4.3. Здесь использованы следующие обозначения:   - погрешность измерения;   - плотность распределения погрешностей  ;   - функция распределения погрешностей,  . Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины   описывается функцией  , где   - среднеквадратическая погрешность.

Если погрешность измерения   находится внутри интервала  , то вероятность этого события вычисляется как

.

(4.35)

В наиболее типичном случае симметричных границ ( ) получим

.

(4.36)

Здесь использовано свойство симметрии функции распределения для закона Гаусса.

Таким образом, если задан интервал  , который содержит в себе погрешность измеряемого параметра  , то вероятность того, что погрешность   не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность   называют также надежностью оценки погрешности и обозначают символом  :

.
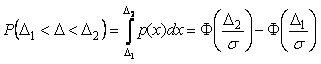