2. Задача о производительности труда

Пусть функция u=u(t) выражает количество произведенной продукции u за время t и необходимо найти производительность труда в момент времени t_0.

За период времени от t₀ до (t₀+t) количество произведенной продукции изменится от значения u₀=u(t₀) до значения u₀+u=u(t₀+t); тогда средняя производительность труда на этот период времени . Очевидно, что производительность труда в момент t₀ можно определить как предельное значение средней производительности за период времени от t₀ до t₀+t при , т.е.

.

- 2 -

Определение. Производной функции у=f(х) в точке х₀ называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, т.е.

.

Производная функции также может быть обозначена одним их символов .

Функция у=f(х), имеющая производную в каждой точке интервала (a;b) называется дифференцируемой в этом интервале; операция нахождения производной функции называется дифференцированием.

Производная функции у=f(х) может быть найдена по схеме:

1. Дадим аргументу х приращение х≠0 и найдем наращенное значение функции у+у=f(х+х).

2. Находим приращение функции у= f(х+х)-f(х).

3. Составляем отношение .

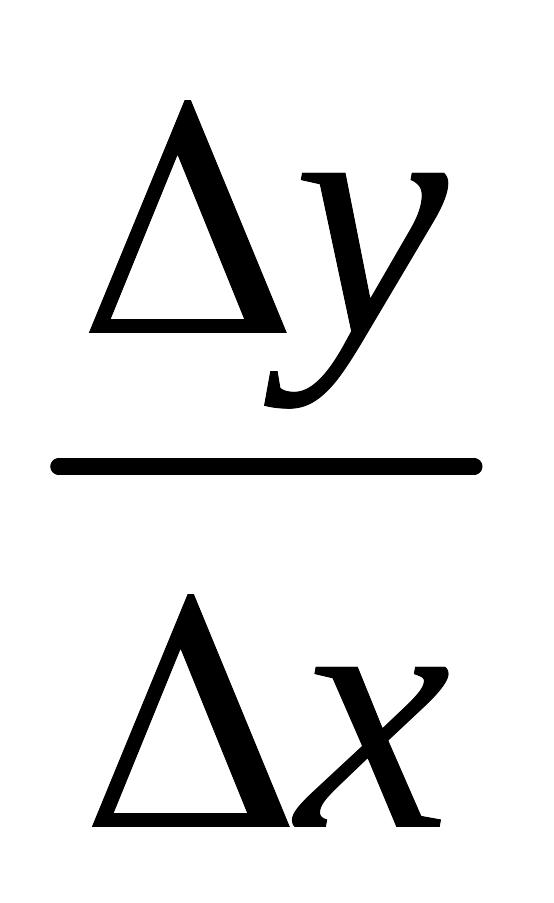4. Находим предел этого отношения при , т.е. 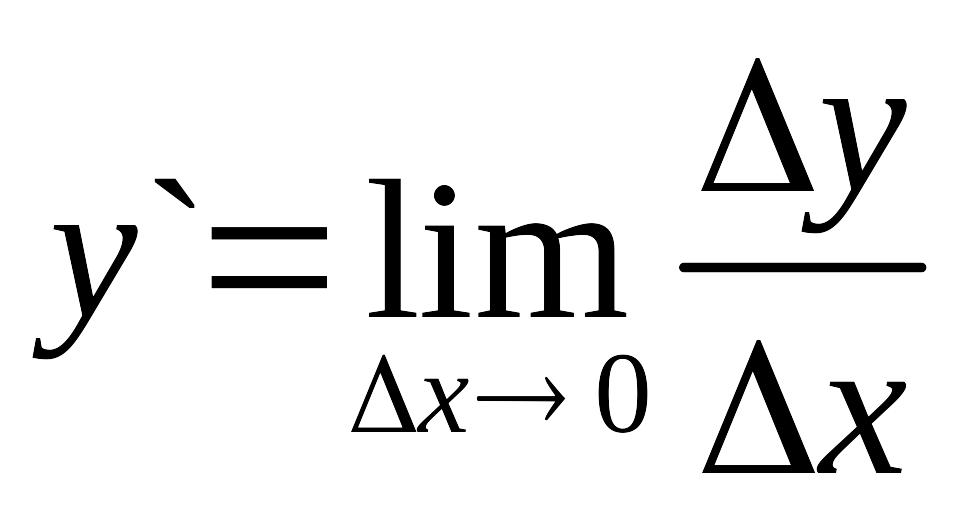(если этот предел существует).

Пример. Используя определение найти производную функции у=х³..

Решение.

1. Дадим аргументу х приращение х≠0 и найдем наращенное значение функции у+у=(х+х)³.

2. Находим приращение функции у=(х+х)³-х³=х³+3х²х+3хх²+х³-х³=х(3х²+3хх+х²).

3. Составляем отношение =3х²+3хх+х².

4. Находим предел = 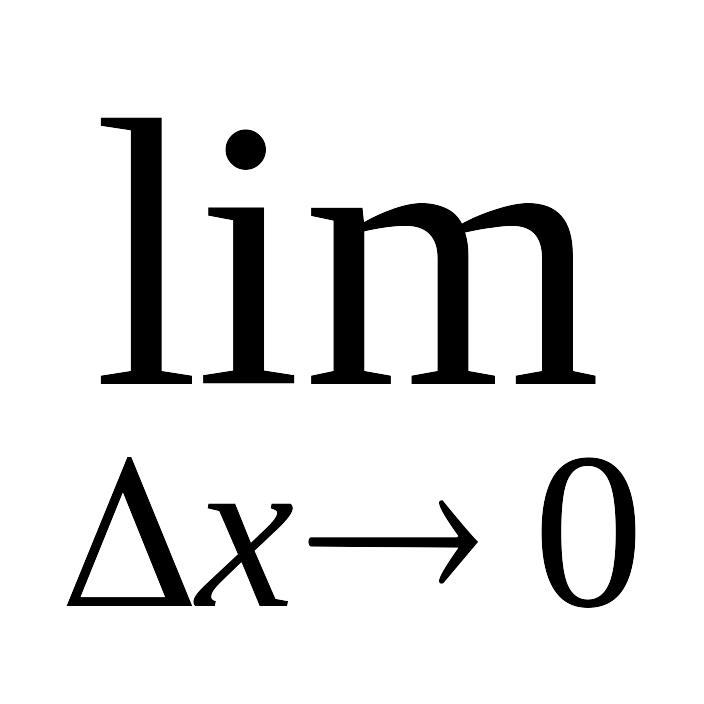(3х²+3хх+х²)= 3х².

Теорема. Если функция дифференцируема в некоторой точке, то она непрерывна в ней.

Обратная теорема неверна: непрерывная функция может не иметь производной.

§ 2. Правила дифференцирования

1. Правила дифференцирования.

2. Производные сложной и обратной функций.

3. Производные основных элементарных функций, таблица производных.

4. Производные высших порядков.

- 1 -

Нахождение производной функции непосредственно по определению часто связано с определенными трудностями. На практике функции дифференцируют с помощью ряда правил и формул.

Пусть функции u=u(x) и - две дифференцируемые на некотором интервале (a;b) функции.

Теорема 1. Производная суммы (разности) двух функций:

. (1)

Теорема справедлива для любого конечного числа слагаемых.

Теорема 2. Производная произведения двух функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:

. (2)

Следствие 1. Постоянный множитель можно выносить за знак производной: .

Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: .

Теорема 3. Производная частного двух функций , если ≠0 равна дроби, числитель который есть разность произведений знаменателя дроби на производную числителя и числителя дроби на производную знаменателя, а знаменатель есть квадрат прежнего знаменателя.

. (3)

Следствие 3. .

Следствие 4. , где с = const.

Пример 1. Найти производную функции и вычислить ее значение в точке х=1.

Решение.

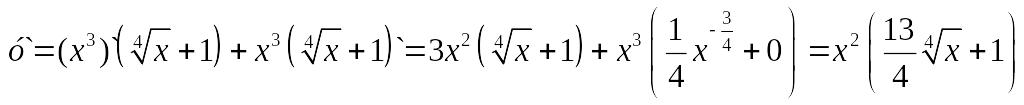
Значение производной в точке х=1 есть .

- 2 -

Пусть переменная y есть функция от переменной u , то есть у=f(u), а переменная u в свою очередь есть функция от независимой переменной х, то есть задана сложная функция .

Теорема 4. Если функция имеет производную в точке х, а функция у=f(u) имеет производную в соответствующей точке , то сложная функция имеет производную в точке х, которая находится по формуле

. (4)

Итак, для нахождения производной сложной функции надо производную данной функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Это правило остается в силе, если промежуточных аргументов несколько. Так, если у=f(u), , , то .

Пусть y=f(x) и - взаимно-обратные функции.

Теорема 5. Если функция y=f(x) строго монотонна на интервале (a;b) и имеет неравную нулю производную в произвольной точке этого интервала, то обратная ей функция также имеет производную в соответствующей точке, определяемую равенством

или .

Таким образом, производная обратной функции равна обратной величине производной данной функции.

Пример 2. Найти производную функции .

Решение. Данная функция является сложной. Ее можно представить в виде цепочки простых функций: , где , где , где . По правилу дифференцирования сложной функции получаем

Пример 3. Пользуясь правилом дифференцирования обратной функции, найти производную для функции .

Решение. Обратная функция имеет производную . Следовательно

.

- 3 -

Таблица производных элементарных функций

№ п/п	Функция у		Производная	№ п/п	Функция	Производная
1	с		0	13
2	х		1	14
3				15
4				16
5				17
6				18
7				19
8				20
9				21
10	,			22
11				23
12				24
				25

-4-

Производная функции y=f(x) есть также функция от х и называется производной первого порядка.

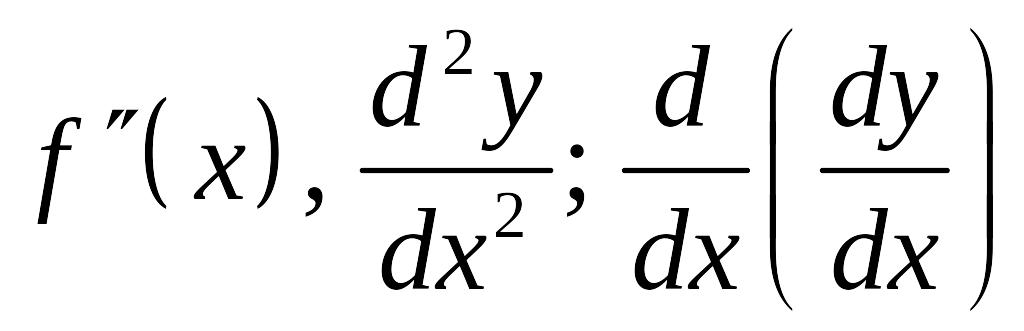Если функция дифференцируема, то ее производная называется производной второго порядка и обозначается (или . Итак, .

Производная от производной второго порядка, если она существует, называется производной третьего порядка и обозначается .

Производной n-го порядка (или n-й производной) называется производная от производной (n-1) порядка:

.

Производные порядка выше первого называются производными высших порядков.

Начиная с производной четвертого порядка, производные обозначают римскими цифрами или числами в скобках (y^V или y⁽⁵⁾). .