§ 2. Основные методы интегрирования
ПЛАН
1. Метод непосредственного интегрирования.
2. Метод интегрирования подстановкой (заменой переменной).
3. Метод интегрирования по частям.
-1-
Метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам называется непосредственным интегрированием.
При сведении данного интеграла к табличному часто используются следующие преобразования дифференциала (операция «подведения под знак дифференциала»):
1. Выражение не изменяется, если под знаком дифференциала к функции прибавить постоянную величину, т.е.
du=d(u+С), где С- число.
2. Если под знаком дифференциала функцию умножить на постоянную величину, все выражение нужно разделить на эту же постоянную величину, т.е.
где С
– число.
Формула
очень
часто используется при вычислении
интегралов. Например,
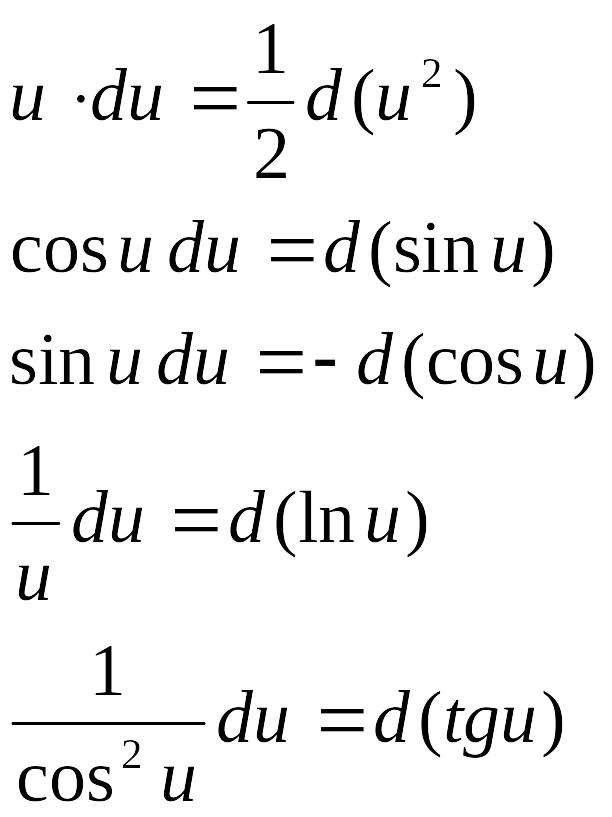
Примеры:
1.
.
2.
.
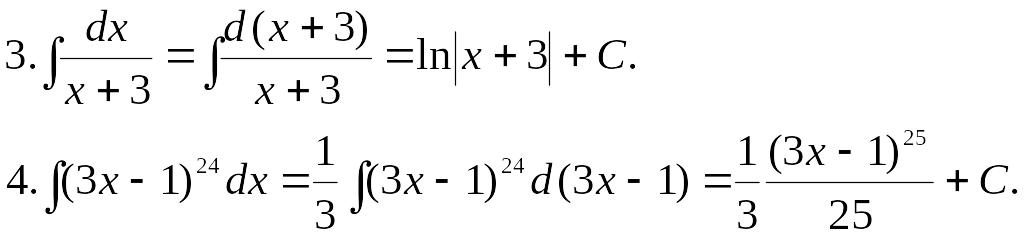
5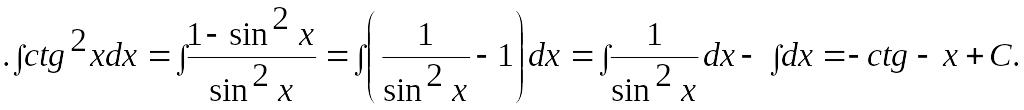
6.
.
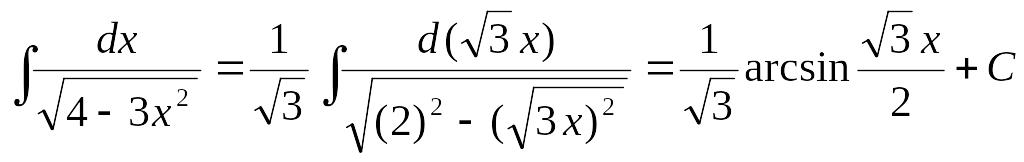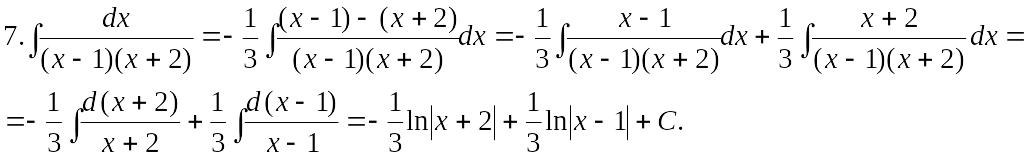
Как видно, вычисление интегралов иногда требует некоторой изобретательности, так сказать «индивидуального подхода к каждой подынтегральной функции». Соответствующие навыки приобретаются в результате значительного числа упражнений.
-2-
Метод интегрирования подстановкой заключается во введение новой переменой интегрирования (т.е. подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся (в случае «удачной» подстановки). Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть
требуется вычислить интеграл
Сделаем подстановку
где
-
функция, имеющая непрерывную производную.
Тогда
и получаем формулу интегрирования
подстановкой
.
(1)
Пример
1:
Найти
.
Решение: Положим х=4t, тогда dx=4dt. Следовательно,
.
Пример
2:
Найти
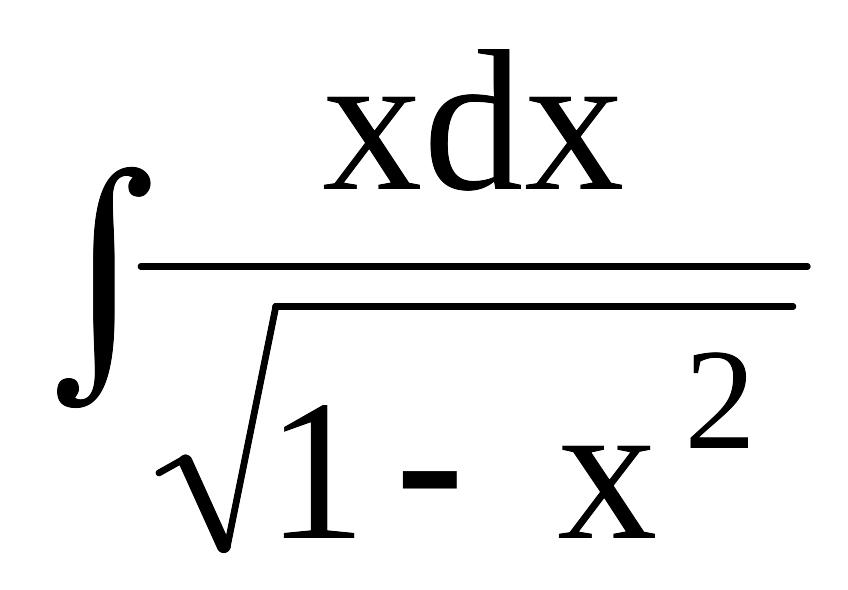
Решение:
Положим t=1-x2.
Тогда
,
.
Следовательно,
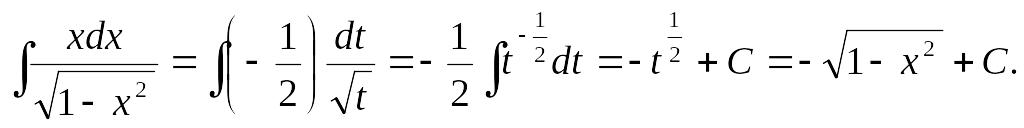
Пример
3.
Найти
Решение:
Обозначим
lnx=t,
тогда
Следовательно,
-3-
Пусть
u=u(x)
и v=v(x)
– функции, имеющие непрерывные
производные. Тогда по правилу
дифференцирования произведения имеем:
.
Интегрируя
это равенство, получим
или
(2)
Полученная
формула называется формулой
интегрирования по частям. При
ее применении подынтегральное выражение
искомого интеграла разбивается на два
сомножителя (u
и dv).
При переходе к правой части (2)
первый из них дифференцируется (
),
второй интегрируется
.
Иногда эту формулу приходиться
использовать несколько раз.
Пример
4:
Найти
Решение:
Пусть
(можно
положить С=0) Следовательно, по формуле
интегрирования по частям:
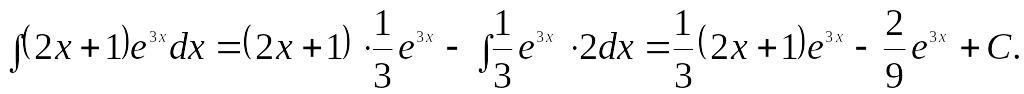
Пример
5:
Найти
Решение:
Пусть
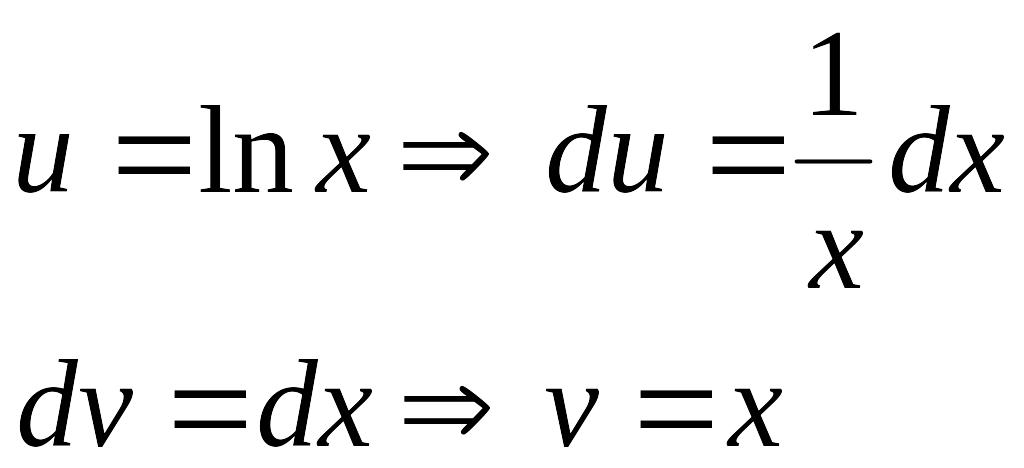
Поэтому:
.
Пример
6:
Найти
Решение:
Пусть
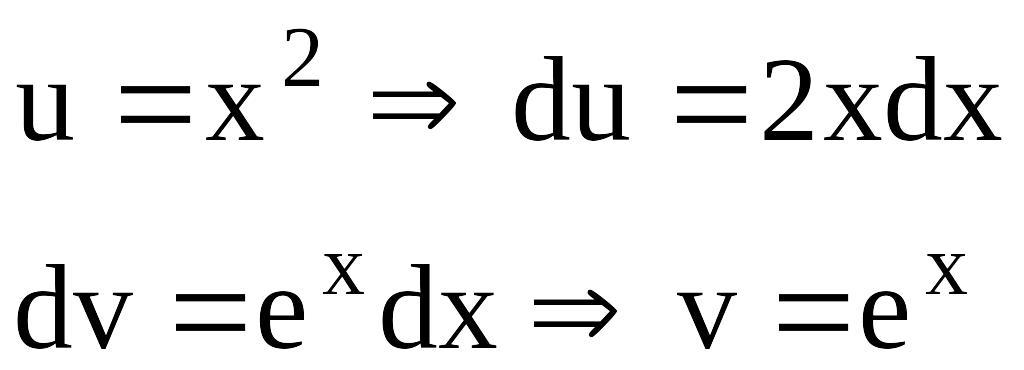
Поэтому:
Для
вычисления интеграла
,
снова применим метод интегрирования
по частям: u=x,
dv=ex
dx
v=ex
Значит,
Поэтому:
.
Пример:
Найти
x
dx
Решение:
Пусть
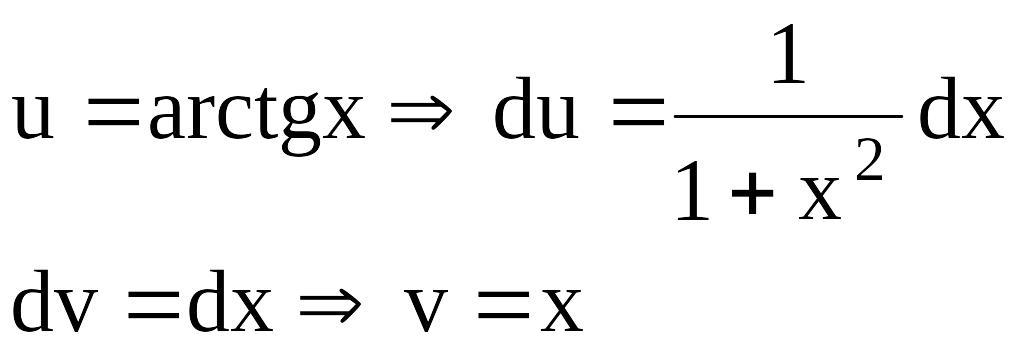
Поэтому:
=
.