Колоквиум 1

§1. Понятие и способы задания функций. Основные свойства функции. Сложная и обратная функции.

О.1. Пусть даны два непустых множества и . Соответствие (закон) , которое каждому элементу сопоставляет один и только один элемент , называется функцией и записывается или .

При этом является независимой переменной или аргументом, - зависимой переменной или значением функции, множество называется областью определения (или существования) функции, множество - областью значений функции, а буква f обозначает закон соответствия.

Функция может быть задана тремя основными способами: аналитически, таблично или графически.

Например:

1) функция (антье) – целая часть, где n – наибольшее из целых чисел не превосходящее аргумента .

2) функция - дробная часть числа: .

Рассмотрим основные свойства функций.

1. Четность и нечетность. Функция , определенная на множестве D называется чет­ной, если для любых значений и нечетной, если . Иначе функ­ция называется функцией общего вида.

График четной функции симметричен относительно оси ординат, а гра­фик нечетной функции симметричен относительно начала координат.

2. Монотонность. Функция называется возрастающей (убывающей) на промежутке , если большему значению аргумен­та из этого промежутка соответствует большее (меньшее) значе­ние функции.

Т.е. если и , то функция возрастает; если и , то функция убывает.

Если и то функция называется неубывающей, если и , то функция называется невозрастающей.

Функции возрастающие, убывающие, неубывающие, невозрастающие называются монотон­ными функциями. Функции возрастающие, убывающие, называются строго монотон­ными функциями.

3. Ограниченность. Функция , определенная на множестве называется ограниченной сверху (снизу) на этом множестве, если существует число , такое что для всех выполняется неравенство . Иначе функция называется неограниченной.

Число и любое большее (меньшее) число называется верхней (нижней) гранью множества значений функции , а наименьшее (наибольшее) из чисел, ограничивающих множество сверху (снизу), - точной верхней (нижней) гранью функции на множестве .

Например, функция ограничена на всей числовой оси, так как для любого .

4. Периодичность. Функция , определенная на множестве , называется периодической на этом множестве, если существует такое число , что при любом значение и . При этом число называется периодом функции.

Если - период функции, то ее периодами будут также числа , где

За основной период берут наименьшее положительное число Т, удовлетворяющее равенству .

Если функции и периодические с периодами и соответственно, то периодом их суммы, произведения, разности и частного является число , кратное и .

5. Явные и неявные функции. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной; напри­мер, функция у=х² +5х + 1. Функция аргумента называется неявной, если она задана уравнением , не разрешенным относительно зависимой переменной. Например, функция у(у>0), заданная уравнением х⁵ + у² - х =0.

6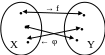 . Обратная функция. Пусть есть функция от независи­мой переменной , определенной на множестве с областью значений . Поставим в соответствие каждому единственное значение , при котором . Тогда полученная функция , определенная на множестве с областью значений , называется обратной.

Обратную функцию обозначают так же в виде . Например, для функции у=а^х обратной будет функ­ция х=log_aу или (в обычных обозначениях зависимой и незави­симой переменных) у= log_a x .

Таким образом, функция имеет обратную, тогда и только тогда, когда выполняется взаимно-однозначное соответствие между множествами и . Отсюда следует, что любая строго монотонная функция имеет обратную. При этом если функция возрастает (убывает), то обратная функция также возрастает (убывает).

Г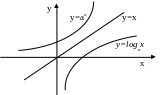 рафики взаимно обратных функ­ций симметричны относительно биссектрисы первого и третьего координатных углов.

7. Сложная функция. Пусть функция есть функция от переменной , определенной на множестве с областью значений , а переменная в свою очередь является функцией от переменной , определенной на множестве с обла­стью значений . Тогда заданная на множестве функция называется сложной функцией.

Переменную называют промежуточным аргументом сложной функции.

Например, — сложная функция, так как ее можно представить в виде , где .