60 Вопрос

Признаки сходимости несобственных интегралов.

1 признак (сравнения).

Е сли хотя бы при выполняется неравенство ; то из сходимости интеграла сходимость а из расходимости интеграла расходимость интеграла .

Д оказательство: Так как сходимость влечет за собой сходимость и наоборот, расходимость . Рассмотрим интегралы на промежутке от до . Возьмём некоторое значение тогда исходя из свойств определённого интеграла, имеем . Переходя в неравенстве к пределу, получим, что несобственный интеграл что если также сходится, то и больший интеграл расходится.

2 признак (предельный признак ).

Е сли выполняется неравенство , и , где - некоторое число не равное 0, , то несобств. интегралы сходятся или расходятся одновременно.

3 признак (признак Коши сходимости несобственных интегралов)

Для сходимости несобственного интеграла необходимо и достаточно, чтобы для любого , можно было бы указать такое число , то для любых чисел превосходящих число выполняется неравенство

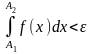
Если сходится интеграл то также сходится, обратное в общем случае неверно, однако если сходится интеграл, то говорят, что, первый интеграл сходиться абсолютно, а - абсолютно интегрируема.

Несобственный интеграл второго рода.

Пусть задана на и не ограниченна на нём, и пусть, кроме того - ограничена и интегрируема на любом отрезке , целиком содержащемся в полу отрезке .

На видим (1). Точка в полу отрезке называется особой точкой функции .

Определение: Правый предел функции (1) при и при условии, что он существует, называется несобственным интегралом второго рода.

(2)

Если предел (2) существует, то говорят, что интеграл сходиться, если конечный предел не существует, то интеграл расходится.

59 Вопрос

Несобственные интегралы.

Рассматривая понятие определенного интеграла существенно выделяли 2 обстоятельства:

1)Отрезок, по которому ведется интегрирование, должен быть конечным.

2)функция , стоящая под знаком интеграла , должна быть должна быть ограничена на отрезке .

Понятие предела позволяет обобщить понятие определенного интеграла на случай бесконечного промежутка интегрирования и на случай неограниченной функции. Соответствующие интегралы называются несобственными интегралами первого и второго рода.

Несобственный интеграл первого рода - интеграл по бесконечному промежутку.

Несобственный интеграл второго рода - интеграл от неограниченной функции.

Несобственные интегралы первого рода.

Могут встретиться три типа бесконечных областей:

1)полупрямая

2)полупрямая

3)вся бесконечная прямая

Рассмотрим функцию , определенную на полупрямой . Пусть A- некоторая точка полупрямой, большая чем а(A>a) и пусть функция интегрируема на отрезке , принадлежащим рассматриваемой полупрямой, тогда на полупрямой можно рассмотреть функцию (1).

Определение: Предел функции при , если он существует, называется несобственным интегралом первого рода от функции по полупрямой и обозначается (2).

При этом говорят, что несобственный интеграл (2) сходится. Если предел бесконечен или не существует, то говорят, что несобственный интеграл расходится. Таким образом: (3).

Если сходится интеграл то также сходится, обратное в общем случае неверно, однако если сходится интеграл, то говорят, что, первый интеграл сходиться абсолютно, а - абсолютно интегрируема.