43. Кратчайшее дерево на графе

Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рёбер.

Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них перечислены ниже:

Алгоритм Прима;

Алгоритм Краскала (или алгоритм Крускала).

Алгоритм Прима

Алгоритм Прима обладает тем свойством, что ребра в множестве А всегда образуют единое дерево. Дерево начинается с произвольной корневой вершины г и растет до тех пор, пока не охватит все вершины в V. На каждом шаге к дереву А добавляется легкое ребро, соединяющее дерево и отдельную вершину из оставшейся части графа. Данное правило добавляет только безопасные для А ребра; следовательно, по завершении алгоритма ребра в А образуют минимальное остовное дерево. Данная стратегия является жадной, поскольку на каждом шаге к дереву добавляется ребро, которое вносит минимально возможный вклад в общий вес.

Алгоритм Краскала

Алгоритм Крускала находит безопасное ребро для добавления в растущий лес путем поиска ребра (u, v) с минимальным весом среди всех ребер, соединяющих два дерева в лесу. Обозначим два дерева, соединяемые ребром (u, v), как С₁ и С₂. (u, v) — безопасное для С₁ ребро. Алгоритм Крускала является жадным, поскольку на каждом шаге он добавляет к лесу ребро с минимально возможным весом.

44. Критический путь на графе

Критический путь графа – это путь максимальной длины в ориентированном ациклическом графе.

При аналитическом задании графа нахождение длины его критического пути как функции внешних параметров задачи является одной из важных задач при распараллеливании алгоритмов. При этом даже в случае, когда алгоритм относится к простому, например, линейному классу, заранее нельзя предугадать, к какому классу функций будет относиться длина критического пути. Один из способов определения длины критического пути предполагает движение от конечной вершины к начальной с определением в процессе движения наиболее раннего времени наступления события.

Критическим путем сетевого графика называется любой путь (то есть последовательность взаимосвязанных событий), ведущий из начального события в конечное событие и целиком состоящий из работ, задержка которых на время ∆t вызовет задержку окончания всего проекта на ∆t времени. Таким образом, для своевременного окончания проекта все события на критическом пути должны быть выполнены без задержек. Критический путь может быть определен как путь из начального в конечное событие, имеющий нулевой резерв времени (нет резерва времени).

Для нахождения критического пути на сетевом графике необходимо оценить резервы времени (ресурсов) для событий (работ) графика: определить для каждого события наиболее ранний и наиболее поздний сроки его наступления (из всех возможных, допускающих окончание всего проекта в срок).

45. Потоки в сетях в принятии решений

Задачи теории потоков в сетях являются одними из основных в исследовании операций, computer science и инженерном деле.

К теории потоков относятся различные задачи, которые можно классифицировать следующим образом. Задачи транспортного типа – транспортная задача, поиск пути минимальной длины, поиск циклов отрицательного веса (неоптимальных перевозок) и т. д. Задачи определения существования потока – задача о максимальном потоке и, двойственная к ней, задача поиска минимального разреза. А также задача о поиске обобщенного потока – потока с потерями и приобретениями.

В 1956 году классическая задача поиска максимального потока была поставлена Фордом и Фалкерсоном и записана уже не в терминах задачи линейного программирования, а в терминах новой теории – теории потоков. Ими же отдельно сформулирована задача поиска максимального потока и предложен первый алгоритм ее решения.

Сетью называется связный граф, в котором заданы “пропускные способности” ребер. Заметим, что сети имеют огромные приложения, в частности, “сети планирования” (имеется в виду планирование производства некоторых новых, достаточно сложных изделий), где “пропускные способности” ребер – это время, за которое нужно из нескольких узлов изделия (вершин графа) получить другой (более сложный) узел.

Потоком в сети между вершиной t (источником) и s (стоком) называется набор чисел c_ij, (т. е. количество условного “груза”, перевозимого из вершины с номером i в вершину с номером j), удовлетворяющих четырем условиям:

1) числа c_ij Ј 0, причем если c_ij > 0, то c_ji = 0 (нет встречных перевозок);

2) числа c_ij Ј q_ij (соответствующих пропускных способностей ребер);

3) если вершина с номером i – промежуточная (не совпадает с источником и стоком), то

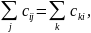
т. е. количество “груза”, вывозимого из вершины i, равно количеству “груза”, ввозимого в эту вершину;

4) количество “груза”, вывозимого из источника t, должно быть равно количеству груза, ввозимого в сток s:

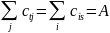
Число А называется величиной данного потока или просто потоком между t и s.

Для дальнейшего нужно следующее определение:

Пусть имеется некоторое сечение между вершинами t и s. Тогда величиной сечения называется сумма пропускных способностей ребер, входящих в это сечение. Сечение называется минимальным (максимальным), если его величина минимальна (максимальна).

Теорема Форда – Фалкерсона (1955). Максимальный поток между вершинами t и s равен величине минимального сечения между этими вершинами.

АЛГОРИТМ ФОРДА - ФАЛКЕРСОНА

Алгоритм начинает работу с начального допустимого потока (возможно, нулевого). Затем осуществляются попытки увеличить величину потока с помощью систематического поиска всех возможных цепей из s в t, на которых можно увеличить величину потока (дополняющие цепи).

Поиск дополняющих цепей производится путем расстановки меток, которые указывают, на каких дугах и на сколько можно увеличить поток. Когда найдена одна из таких цепей, поток вдоль нее увеличивается. После чего все метки стираются, и вновь полученный поток используется в качестве исходного при новой расстановке меток.

Алгоритм заканчивает работу, когда нельзя найти ни одну дополняющую цепь. Последний найденный поток является максимальным.

Актуальность задачи о максимальном потоке постоянно возрастает в месте со строительством трубопроводов, новых дорог, роста пользователей Интернета и любых других сетей. Поэтому быстрое и точное её решение крайне необходимо во всех сферах нашей деятельности, где хоть как-то встает вопрос об перемещение чего-либо куда-либо с максимальной рациональностью.