35. Особенности применения методов математического программирования в принятии решений

Метод математического программирования выделен как самостоятельный из числа аналитических методов в силу его значимости при разработке обоснований для стратегических УР.

Метод включает систему формул и правил расчетов для нахождения условных экстремумов при анализе экономических процессов. Такие процессы описываются в виде системы уравнений. Процедура расчетов носит название математического программирования. Суть данного метода заключается в формализации исследуемых процессов и построении математической модели в виде системы уравнений и неравенств. Схематично процесс РУР методом математического программирования можно представить так, как это показано на рисунке.

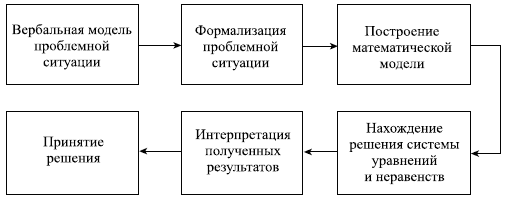
Рис. Модель процесса УР методом математического программирования

Особенность этого метода состоит в том, что он применим только в случаях, когда возможна формализация проблемной ситуации. Но даже в этом случае данному методу отводится вспомогательная роль, а решение принимается с учетом расчетов, которые лишь помогают ЛПР обосновать тот или иной выбор.

Рур-разработка управленческих решений

36. Многокритериальная оптимизация в принятии решений

Многокритериальная оптимизация - это процесс одновременной оптимизации двух или более конфликтующих целевых функций в заданной области определения. Задача многокритериальной оптимизации состоит в поиске вектора целевых переменных, удовлетворяющего наложенным ограничениям и оптимизирующего векторную функцию, элементы которой соответствуют целевым функциям. Эти функции образуют математическое описание критерия удовлетворительности и, как правило, взаимно конфликтуют. Отсюда, «оптимизировать» означает найти такое решение, при котором значение целевых функций были бы приемлемыми для постановщика задачи.

Здесь предполагается, что выбор оптимальных значений х

производится не во всем n-мерном пространстве Rⁿ, а лишь в пределах некоторого его подмножества D. Таким образом, задано m функций или функционалов fi, отображающих множество D n-мерных векторов х=(х₁, …, х_n) во множество вещественных чисел R.

Важнейшее значение при исследовании задач имеет принцип Парето и связанные с ним понятия эффективного (Парето-оптимального) и слабо эффективного решения.

Множество состояний системы, оптимальных по Парето, называют «множеством Парето», «множеством альтернатив, оптимальных в смысле Парето», либо «множеством Парето-оптимальных альтернатив». Ситуация, когда достигнута эффективность по Парето — это ситуация, когда все выгоды от обмена исчерпаны.

Методы многокритериальной оптимизации

Метод главного критерия

В методе главного критерия в качестве целевой функции выбирается один из функционалов наиболее полно с точки зрения исследователя отражающий цель принятия решения

Метод линейной свёртки

Метод линейной свёртки позволяет заменить векторный критерий оптимальности на скалярный. Он основан на линейном объединении всех частных целевых функционалов в один.

Метод максимальной свёртки

Здесь, в отличие от метода линейной свертки, на целевой функционал оказывает влияние только тот частный критерий оптимальности, которому в данной точке соответствует наименьшее значение соответствующей функции.