31. Динамическое программирование в принятии решений.
Динамическое программирование в теории управления и теории вычислительных систем — способ решения сложных задач путём разбиения их на более простые подзадачи. Он применим к задачам с оптимальной подструктурой, выглядящим как набор перекрывающихся подзадач, сложность которых чуть меньше исходной. В этом случае время вычислений, по сравнению с «наивными» методами, можно значительно сократить.
Ключевая идея в динамическом программировании достаточно проста. Как правило, чтобы решить поставленную задачу, требуется решить отдельные части задачи (подзадачи), после чего объединить решения подзадач в одно общее решение. Часто многие из этих подзадач одинаковы. Подход динамического программирования состоит в том, чтобы решить каждую подзадачу только один раз, сократив тем самым количество вычислений. Это особенно полезно в случаях, когда число повторяющихся подзадач велико.
Метод динамического программирования сверху — это простое запоминание результатов решения тех подзадач, которые могут повторно встретиться в дальнейшем. Динамическое программирование снизу включает в себя переформулирование сложной задачи в виде рекурсивной последовательности более простых подзадач.
Оптимальная подструктура в динамическом программировании означает, что оптимальное решение подзадач меньшего размера может быть использовано для решения исходной задачи.
Подзадачи решаются делением их на подзадачи ещё меньшего размера и т. д., пока не приходят к тривиальному случаю задачи, решаемой за константное время (ответ можно сказать сразу).
Перекрывающиеся подзадачи в динамическом программировании означают подзадачи, которые используются для решения некоторого количества задач (не одной) большего размера (то есть мы несколько раз проделываем одно и то же).
Подводя итоги вышесказанного можно сказать, что динамическое программирование пользуется следующими свойствами задачи:
перекрывающиеся подзадачи;
оптимальная подструктура;
возможность запоминания решения часто встречающихся подзадач.
Динамическое программирование обычно придерживается двух подходов к решению задач:
нисходящее динамическое программирование: задача разбивается на подзадачи меньшего размера, они решаются и затем комбинируются для решения исходной задачи. Используется запоминание для решений часто встречающихся подзадач.
восходящее динамическое программирование: все подзадачи, которые впоследствии понадобятся для решения исходной задачи просчитываются заранее и затем используются для построения решения исходной задачи.
32. Нелинейное программирование в принятии решений.
Нелинейное программирование - раздел математического программирования, изучающий методы решения экстремальных задач с нелинейной целевой функцией и (или) областью допустимых решений, определенной нелинейными ограничениями.
Общая задача нелинейного программирования (ОЗНП) определяется как задача нахождения максимума (или минимума) целевой функции f (x1, х2 ..., x n ) на множестве D, определяемом системой ограничений
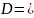(2,1)
где хотя бы одна из функций f или gi является нелинейной.
По аналогии с линейным программированием ЗНП однозначно определяется парой (D, f) и кратко может быть записана в следующем виде
(2,2)
Особенности нелинейного программирования
1)Задачи НЛП значительно ближе к реальным ситуация, чем линейные;
2)Задачи НЛП могут быть с ограничениями и без них;
3)Множество допустимых планов D может иметь очень сложную структуру (например, быть невыпуклым или несвязным);
4)Глобальный максимум (минимум) может достигаться как внутри множества D, так и на его границах;
5)Целевая функция f может быть недифференцируемой, что затрудняет применение классических методов математического анализа;
6)Задачи НЛП настолько разнообразны, что для них не существует общего метода решения.
Источники нелинейности относятся в основном к одной из двух категорий:
1) Реально существующие и эмпирически наблюдаемые нелинейные соотношения.
2) Установленные (постулируемые) руководством правила поведения или задаваемые зависимости.
Задача нелинейного программирования встречается в естественных науках, технике, экономике, математике, в сфере деловых отношений и в науке управления государством.
Метод "затраты – эффективность" также укладывается в схему нелинейного программирования.
Данный метод был разработан для использования при принятии решений в управлении государством.
Классификация методов нелинейного программирования
По количеству локальных критериев в целевой функции:
1)однокритериальные
2)многокритериальные
По длине вектора :
1)однопараметрические или одномерные (n=1),
2)многопараметрические или многомерные (n>1).
По наличию ограничений:
1) без ограничений (безусловная оптимизация),
2)с ограничениями (условная оптимизация).
По типу информации, используемой в алгоритме поиска экстремума: методы прямого поиска, т.е. методы, в которых при поиске экстремума целевой функции используются только ее значения;
градиентные методы первого порядка, в которых при поиске экстремума функции используются значения ее первых производных;
градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.
градиентные методы второго порядка, в которых при поиске экстремума функции наряду с первыми производными используются и вторые производные.