24. Двойственная задача линейного программирования.

Перенесем все неизвестные модели в левую часть и справа (за чертой) запишем переменные двойственной задачи, соответствующие каждому ограничению исходной задачи:

max Z

a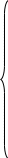 ₁₁x₁+ a₁₂x₂ +…+ a_1nx_n A₁ y₁

a₂₁x₁ + a₂₂x₂ +…+ a_2nx_n A₂ y₂

…………………………... …

a_m1x₁+ a_m2x₂ +…+ a_mnx_n A_m y_m

-b₁₁x₁ -b₁₂x₂ -…-b_1nx_n+ k₁Z0 y_m+1

-b₂₁x₁-_b22x2 -… -b_2nx_n+ k₂Z0 y_m+2

…………………………... …

-b_r1x₁-b_r2x₂ -… -b_{r n}x_n+k_rZ0 y_m+r

x_i0

i=1,2,…,n

Двойственная задача линейного программирования в данном случае имеет вид:

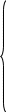m in (A₁y₁+A₂y₂ +…+A_my_m )

a₁₁y₁+a₂₁y₂+…+a_m1y_m-b₁₁y_m+1 – b₂₁y_m+2 -…-b_r1y_m+r0

a₁₂y₁+a₂₂y₂+…+a_m2y-b₁₁y_m+1 – b₂₂y_m+2 -…-b_r2y_m+r0

………………………….……………………………..

a_1ny₁+a_2ny₂+…+a_mny_m-b_1ny_m+1 – b_2ny_m+2 -…-b_{r n}y_m+r0

k₁ y_m+1 + k₂ y_m+2 +…+k_r y_m+r1

y_i0

i=1,2,…,m+r.

Далее необходимо обратиться к следующей теореме линейного программирования:

Если какое-либо ограничение исходной задачи линейного программирования выполняется как строгое неравенство, то соответствующая переменная в двойственной задаче равна 0.

Справедлива и обратная теорема.

Если оптимальный план удается построить в рамках данной модели, то последняя система математических соотношений называется принципом оптимальности плана.

Равенство k₁y_m+1 + k₂y_m+2 +…+k_ry_m+r может быть условием проверки, так как k₁,k₂,…,k_r известны.

Также важно, что целевые функции прямой и двойственной задач равны:

max Z=min (A₁y₁+A₂y₂ +…+A_my_m ).

25. Модель оптимального планирования производства.

Постановка задачи оптимального планирования

Планирование — важнейший этап экономической и управленческой деятельности. Объектом планирования может быть деятельность подразделения или всего предприятия, отрасли промышленности или сельского хозяйства, региона, наконец, государства.

Постановка задачи планирования в общем случае выглядит следующим образом:

имеются некоторые плановые показатели: X, Y, ...;

имеются некоторые ресурсы: R₁, R₂, ..., за счет которых эти плановые показатели могут быть достигнуты;

имеется определенная стратегическая цель, зависящая от значений  плановых показателей,  на которую следует ориентировать планирование.

Задача оптимального планирования заключается в определении значений плановых показателей с учетом ограниченности ресурсов при условии достижения стратегической цели.

Вопрос о стратегических целях в этом случае очень сложен. У государства их много, но в разные периоды истории приоритеты могут меняться. Например, в военное время главной целью является максимальная обороноспособность, военная мощь страны. В мирное время в современном цивилизованном государстве приоритетной целью должно быть достижение максимального уровня жизни населения.

Решение задач оптимального планирования чаще всего является сложным и недоступным при использовании лишь человеческого опыта (эмпирических методов). Для решения таких задач строится математическая модель, устанавливающая связь между параметрами задачи. Следовательно, оптимальное планирование осуществляется путем применения математического моделирования. Как правило, такие модели для реальных ситуаций не поддаются аналитическому решению, поэтому используются численные методы решения, реализуемые на компьютере.