
- •1.Событием называется любой факт, который в результате опыта может произойти или не произойти.
- •2. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
- •Гипергеометрическое распределение
- •Показательное (экспоненциальное распределение)
- •Условные законы распределения составляющих дискретной двумерной случайной величины.
- •Неравенство Чебышева
- •Теорема Чебышева(основное утверждение збч)
- •Теорема Бернулли
- •Доверительный интервал для мат. Ожидания при известной дисперсии.
- •32.Критерий Стьюдента (t-критерий)
- •А) случай независимых выборок
- •Б) случай связанных (парных) выборок
- •33. Дисперсионный анализ.
- •34. Дисперсионный анализ.
- •37.Пусть св z зависит от нескольких параметров . Предположим, что зависимость линейная , т.Е. Структура аппроксимирующей функции
- •40.Рассмотрим некоторую систему s, которая проходит случайный процесс , т.Е. С течением времени система переходит из одного состояния в др. → →…..
1.Событием называется любой факт, который в результате опыта может произойти или не произойти.
Опытом или испытанием или экспериментом называется выполнение определенного комплекса условий.
События делятся на достоверные, невозможные и случайные.
Событие называется достоверным, если оно обязательно произойдет в результате испытания(р=1). Событие называется невозможным, если оно заведомо не произойдет в результате испытания(р=0). Событие называется случайным, если оно в результата опыта может произойти, а может и не произойти.
Элементарным событием называют всякий исход опыта. Составное, если возможно несколько исходов. Элементарные события, входящие в состав составного события, называются благоприятствующими.
Два события называются совместными, если в результате испытания появление одного из них не исключает появление другого. Два события называются несовместными, если в результате испытания появление одного из них исключает появление другого.
2. С событиями связываются некоторые числа, характеризующие степень объективной возможности появления этих событий, называемые вероятностями событий.
Классическое определение вероятности: отношение числа благоприятствующих событий к общему числу элементарных исходов испытания. Р(А)=m/n. m-число благоприятствующих исходов, n-общее число исходов.
Геометрическое: вероятность случайного события А равна отношению меры области, благоприятствующей появлению события А, к мере всей области. Р(А)=ω(А)/Ω, ω(А)-пространство исходов благоприятствующих событий А, Ω-пространство всех элементарных исходов испытания.
Статистическое:
статистическая
вероятность случайного события А равна
относительной частоте появления этого
события в ряде испытаний.
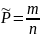 ,m –
число испытаний, в которых появилось
событие А; n – общее число
испытаний.
,m –
число испытаний, в которых появилось
событие А; n – общее число
испытаний.
3.Для несовместных событий:
Суммой двух событий А и В называется событие, состоящее из наступлений или А, или В.Р(А+В)=Р(А)+Р(В)
Для совместных событий:
Р(А+В)=Р(А)+Р(В)-Р(А*В)
События называются независимыми, если наступление одного из них не влияет на наступление другого.
Произведением двух событий А и В называется событие, состоящее из наступлений и А, и В.
Р(А*В)=Р(А)*Р(В)
Зависимые:
Р(А*В)=Р(А)*Р(В/А)
4.Для расчета числа элементарных событий используют формулы комбинаторики:
Без повторений: C повторениями:
Сочетание---
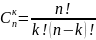
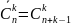
Размещение---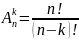 (важен порядок)
(важен порядок)
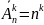
Перестановка---
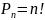
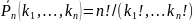
5. Условная вероятность — это вероятность некоторого события A, при условии наступления некоторого другого события B. Р(А/В)
Формула полной вероятности:
Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2, ..., Hn, образующих полную группу. Тогда вероятность события A определяется как сумма произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:
Р(А)=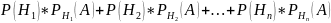
6. Условная вероятность — это вероятность некоторого события A, при условии наступления некоторого другого события B. Р(А/В)
Формула Байеса:
Предположим, что событие A может наступить лишь при появлении одного из несовместных событий (гипотез) H1, H2, ..., Hn, образующих полную группу. Событие A уже произошло. Требуется вычислить условные вероятности гипотез (при условии, что событие А произошло).
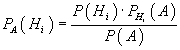
7.Пусть некоторое испытание повторяется n раз. В результате испытания событие А может произойти с вероятностью Р или не произойти с вероятностью q=1-p.
Задачу расчета вероятностей числа наступления события А называют схемой Бернулли: где k-кол-во наступлений события А
![]()
8.
Если
при наличии схемы Бернулли число
испытаний n велико, а вероятность
наступления события p мала, то вместо
формулы Бернулли используют формулу
Пуассона:
![]()
Локальная теорема Муавра — Лапласа. Если в схеме Бернулли число n велико,а число p отлично от 0 и 1, тогда:

Функция φ(x) называется функцией Гаусса(четная).
Интегральная
теорема Лапласа:
Если n – велико, а р – отлично от 0 и 1,
то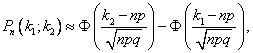
9.Величина, принимающая свои значения с некоторой вероятностью называется случайной.
Если значения случайной величины образуют конечное или счетное множество, то ее называют дискретной.
Если значения образуют несчетное множество, то случайную величину называют непрерывной.
Случайную величину Х можно определить как некоторую функцию, заданную на пространстве элементарных событий Ω.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn:
хi |
x1 |
x2 |
... |
xn |
pi |
p1 |
p2 |
|
pn |
10. Сумма произведений всех возможных значений случайной величины на вероятности этих значений называется математическим ожиданием случайной величины и обозначается М(X).
М(Х)=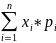
Свойства математического ожидания случайной величины:
1) Математическое ожидание постоянной величины равно самой величине: М[C]=C.
2)Постоянный множитель можно выносить за знак математического ожидания: М[C×Х]=C×M[X].
3)Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин: М[Х+Y]=M[X]+M[Y].
4)Математическое ожидание произведения двух независимых случайных величин равно произведению математических ожиданий этих величин: М[Х×Y]=M[X]×M[Y].
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.
![]()
Свойства дисперсии случайной величины:
1. Дисперсия постоянной величины равна нулю: D[C]=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D[C×Х]=C2×M[X].
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D[Х+Y]=D[X]+D[Y].
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин: D[Х–Y]=D[X]+D[Y].
Средним квадратическим отклонением случайной величины X называется квадратный корень из дисперсии:
![]() .
.
Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность.
Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е. Р(Х < Ме) = Р(X > Ме)(не вычисляется для дискретных величин).
Начальным
моментом k-го
порядка
случайной величины Х называется
математическое ожидание величины 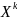 ,
т.е.V(x) = М(
,
т.е.V(x) = М( ).
Начальный момент первого порядка – это
математическое ожидание случайной
величины.
).
Начальный момент первого порядка – это
математическое ожидание случайной
величины.
Центральным моментом k-го порядка μk случайной величины Х называется математическое ожидание величины (Х–М(Х))k, т.е. μk = М(Х–М(Х))k. Центральный момент второго порядка – это дисперсия случайной величины.
Величина As = μ3 / σ3 называется коэффициентом асимметрии.
Эксцессом Еk называется величина Еk = μ4 / σ4 – 3.
Квантилью xp случайной величины , имеющей функцию распределения F (x), называют решение xp уравнения F (x) = p. медиана - квантиль уровня 0.5; нижняя квартиль - квантиль уровня 0.25; верхняя квартиль - квантиль уровня 0.75.
11.Пусть
производится n
независимых испытаний, в которых событие
А может происходить с разными вероятностями:
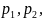 …
…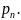 Тогда
Тогда
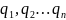 - вероятности невыполнения события А.
Обозначим
- вероятности невыполнения события А.
Обозначим
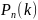 -вероятность
того, что событие А в n
испытаниях выполняется k
раз. Тогда функция
-вероятность
того, что событие А в n
испытаниях выполняется k
раз. Тогда функция
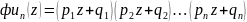 называется
производящей.
Тогда
вероятность
равна коэффициенту
называется
производящей.
Тогда
вероятность
равна коэффициенту
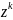 производящей функции.
производящей функции.
Пусть n=2, тогда
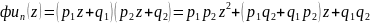 то
есть для 2 испытаний получаем: коэффициент
то
есть для 2 испытаний получаем: коэффициент
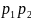 при
при
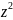 равен вероятности
равен вероятности
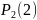 ;
коэффициент
;
коэффициент
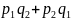 при
при
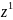 равен вероятности
равен вероятности
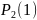 ,
,
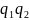 равен
равен
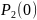 .
.
12. Биномиальный закон распределения: биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения X=k (числа k появлений события) вычисляют по формуле Бернулли: математическое ожидание M(X) = np, дисперсия D(X) = npq.
Закон
распределения Пуассона:
Это распределение представляет собой
предельный случай биномиального, когда
вероятность р очень мала, а число
испытаний n велико.
Дискретная
случайная величина Х, которая может
принимать только целые неотрицательные
значения с вероятностями ![]() где k – число появления событий
в n независимых испытаниях,
где k – число появления событий
в n независимых испытаниях,
λ = n· p (среднее число появлений события в n испытаниях), называется распределенной по закону Пуассона с параметром λ. М(Х) = D( X) = λ.
13. Геометрическое распределение
Для бесконечной последовательности испытаний в схеме Бернулли случайная величина Х, равная числу испытаний до первого успеха включительно, имеет геометрическое распределение
|
|
где p - вероятность успеха. M( х )=1/р, D( X)=q/p^2
X |
1 |
2 |
3 |
… |
n |
… |
P |
p |
qp |
|
… |
|
… |
q=1-p
