17. Пункты лакальнага экстрэмума ф.Д.З. Неабходная і дастатковыя ўмовы існавання лакальных экстрэмумаў.

Няхай ф-ыя z=f(x, y) вызначана на некаторым мн-ве і няхай п.( x₀, y₀)- унутраны п-т мн-ва

Азн.1 П.( x₀, y₀) наз п. лакальнага максімума(мінімума) ф-ыі z=f(x, y), калі існуе наваколле п.( x₀, y₀) для ўсіх п. якога выконваецца ўмова f(x, y) f(x₀, y₀) (f(x, y) f(x₀, y₀)). Калі для любога п.( x, y) (x₀, y₀), то п.(x₀, y₀) – строгага лакальнага максімума(мінімума)

Г авораць, што ф-ыя ў п.(x₀, y₀) мае max i min. П. строгага лакальнага max i min наз п. строгага лакальнага экстрэмума. П. лакальнага max i min – п. лакальнага экстрэмума.

Тэарэма1.(Небходная ўмова існавання экстрэмума): Калі ф-ыя z=f(x, y) дыф у п.(x₀, y₀) і мае у гэтым п-це экстрэмум, то ўсе яе частковыя вытворныя у гэтым п.=0

Д оказ. Няхай ў п.(x₀, y₀) ф-ыя z мае лакальны max, г.зн. . Г.зн., што ф-ыя адной зменнай z=f(x, y₀) мае ў п. x₀ max. Па неабходнай ўмове экстрэмума ф-ыі адной зменнай, тады атрымаем f ‘(x₀, y₀) =0 для f(x, y₀), але гэта вытворная супадае з частковай вытворнай ф-ыі 2-х зменных f(x, y) па зменнай x у п.(x₀, y₀) =>

Аналагічна можна атрымаць, што (1)

Заўвага1. Неабходную ўмову экстрэмума можна запісаць так: калі ў п.(x₀, y₀) дыф ф-ыя мае экстрэмум, то

Заўвага2.Можна заўважыць, што раўнанне датычнай пл-ці ў тым п-це графіка дыф ф-ыі ў якім яна мае экстрэмум мае выгляд z=z₀. Т.ч. датычная пл-ць у п. экстрэмума будзе паралельна пл-ці хОу

Азн.2 П-ты мн-ва у якіх усе частковыя вытворныя ф-ыі f існуюць і=0 наз стацыянарнымі п-мі. П-ты мн-ва у якіх частковыя вытворныя ф-ыі z=0 або наз крытычнымі п-мі.

Заўвага3. З Т.1 і Азн.2 => п. экстрэмума трэба шукаць сярод крытычных п-аў ф-ыі.

Прыклад. Паказвае, што дыф ф-ыя можа не мець экстрэмумы у стацыянарных п.

z =x²+y²

=> (0,0)- стацыянарны п-т. Аднак у дастаткова малым наваколлі п.(0,0) ф-ыя прымае

як дадатнае, так і адмоўнае значэнне

z(0,0)=0

Не выконваецца азначэнне экстрэмума і стацыян п.(0,0) не з’яўляецца экстрэмумам

Тэарэма2.(Дастатковая ўмова экстрэмума): Калі ф-ыя f двойчы непарыўна дыф у стацыянарным п.(x₀, y₀) і калі выконваецца ўмова , то ф-ыя z=f(x, y) мае ў п.(x₀, y₀) экстрэмум: строгі max, калі і строгі min

Калі , то экстрэмума не існуе, калі , то ці існуе, ці не існуе.

Правіла знаходжання найбольшага і найменьшага знач ф-ыі:

Разгледзім дыф ф-ыю z=f(x, y), якая вызначаецца на абмежаваным замкнутым мн-ве Е. Для такой ф-ыі справядліва тэарэма Веерштраса “аб існаванні найбольшага і найменьшага значэн”. Тады са сказанага вышэй можна сфармуляваць наступныя правіла:

1. Знайсці ўсе п. мн-ва Е, якія з’яўл крытычнымі п. для ф-ыі z

2. Вылічыць значэнне ф-ыі ў крытычных п.

3. Вылічыць значэнне ф-ыі ў гранічных п-ах мн-ва Е

4. Параўнаць ўсе атрыманыя знач – выбраць найб і найм

Прыклад1. Знайсці экстрэмум ф-ыі: z=x²+y²+1

=> (0,0)- крытычны п-т

(0,0)-п-т экстрэмума

П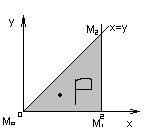 рыклад2. Знайсці найб і найм знач ф-ыі:

1. знойдзем стацыян п-ы

(1,1/2) z(1,1/2)= -

2. M₀M₁: y=0,

M₁M₂: x=2,

z(2,1)=2

z(2,2)=8 найб

z(2,0)=8

3. М₀М₂: х=у,