1. _{Множество и подмножество. Пустое множество. Конечные и бесконечные множества. Объединение, пересечение и разность множеств. Примеры.}

Множество — одно из ключевых понятий математики, в частности, теории множеств и логики. Математика — наука о структурах, порядке и отношениях, которая исторически сложилась на основе операций подсчёта, измерения и описания форм реальных объектов. Теория множеств — раздел математики, в котором изучаются общие свойства множеств. Логика — наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Понятие множества обычно принимается заодно из исходных (аксиоматических) понятий, то есть не сводимое к другим понятиям, а значит, и не имеющее определения. Однако, можно дать описание множества, например, в формулировке Георга Кантора: Под «множеством» мы понимаем соединение в некое целое M определённых хорошо различимых предметов m нашего созерцания или нашего мышления (которые будут называться «элементами» множества M). Другая формулировка принадлежит Бертрану Расселлу: «Множество есть совокупность различных элементов, мыслимая как единое целое». Также возможно косвенное определение через аксиомы теории множеств. В математической логике и дискретной математике часто употребляемый синоним множества — алфавит. Множество может быть замкнутым и незамкнутым, полным и пустым, упорядоченным и неупорядоченным, счётным и несчётным, конечным и бесконечным. Более того, как в наивной, так и в формальной теориях множеств любой объект обычно считается множеством.

• 

Элемент множества. Объекты, из которых состоит множество, называют элементами множества или точками множества. Множества чаще всего обозначают заглавными буквами латинского алфавита, его элементы — строчными. Если а — элемент множества А, то записывают а ∈ А (а принадлежит А). Если а не является элементом множества А, то записывают а ∉ А (а не принадлежит А). В отличие от мультимножества каждый элемент множества уникален, и в множестве не может быть двух идентичных элементов. Иначе говоря, добавление к множеству элементов, идентичных уже принадлежащим множеству, не меняет его: {6, 11} = {11, 6} = {11, 11, 6, 11, 6} Математическое понятие множества элементов принимается в качестве интуитивного. Множество задается правилом или признаком, согласно которому определяем, принадлежит ли данный элемент множеству или не принадлежит. Множество обозначают символом A = {x}, где x - общее наименование элементов множества A. Часто множество записывают в виде A = {a, b, c, ...}, где в фигурных скобках указаны элементы множества A. Будем пользоваться обозначениями: N - множество всех натуральных чисел; Z - множество всех целых чисел; Q - множество всех рациональных чисел; R - множество всех действительных чисел; C - множество всех комплексных чисел; Z0 - множество всех неотрицательных целых чисел.

Аксиоматическая теория множеств Особенностью аксиоматического подхода является отказ от представления о действительном существовании множеств в некотором идеальном мире. В рамках аксиоматических теорий множества «существуют» исключительно формальным образом, и их «свойства» существенно зависят от выбора аксиом. Этот факт всегда являлся мишенью для критики со стороны тех математиков, которые не соглашались (как на том настаивал Гильберт) признать математику лишённой всякого содержания игрой в символы. В частности, Н. Н. Лузин писал, что «мощность континуума, если только мыслить его как множество точек, есть единая некая реальность», место которой в ряду кардинальных чисел не может зависеть от того, признаётся ли в качестве аксиомы континуум-гипотеза, или же её отрицание. На самом деле, вопрос выбора аксиом в данном случае тождественен выбору наших пожеланий к некоторому множеству. А выбор пожеланий — фундаментальный вопрос любого творчества. Так мы подходим к вопросу места желаний в существовании конкретной формы, удовлетворяющей желанию. Что было раньше: курица или яйцо? Так называемая объективность существования объекта (то есть вне нашего представления о нём и отношения к нему) совершенно не означает, что этот объект не был кем-то создан. Скорее, наоборот, у каждого объекта или формы есть свой творец. Значит, когда-то было время, когда каждая форма была на стадии определения требований, которым она должна соответствовать. Этот процесс определения требований был субъективным, а сама форма вообще не существовала в природе, только в воображении творца. Можно задуматься о месте объективности и о том, как и откуда она возникает. Потому, следует более осмотрительно относиться к желаниям вообще (аксиомам на языке математики). Желания иногда осуществляются, это более серьёзно, чем игра математиков с числами (аксиомами). В настоящее время наиболее распространённой аксиоматической теорией множеств является ZFC — теория Цермело — Френкеля с аксиомой выбора. Вопрос о непротиворечивости этой теории (а тем более — о существовании модели для неё) остаётся не решённым. Не всеми математиками аксиома выбора принимается безоговорочно. Так, например Эмиль Борель и Анри Лебег считают, что доказательства, полученные при помощи этой аксиомы, имеют другую познавательную ценность, чем доказательства, независимые от неё. Другие же математики, такие как Феликс Хаусдорф и Адольф Френкель, принимают аксиому выбора безоговорочно, признавая за ней ту же степень очевидности, что и за другими аксиомами Цермело — Френкеля.

Подмножество в теории множеств — это понятие части множества. Определение Множество является подмножеством множества , если любой элемент, принадлежащий , также принадлежит . Формальное определение: Множество называется надмно́жеством множества, если — подмножество. Множество B, все элементы которого принадлежат множеству A, называется подмножеством множества A, и при этом записывают (или) Под множеством мы понимаем объединение в одно целое определенных, вполне различимых объектов нашей интуиции или нашей мысли" — так описал понятие "множество" Георг Кантор, основатель теории множеств. Основные предпосылки канторовской теории множеств сводятся к следующему:1° Множество может состоять из любых различимых объектов.2° Множество однозначно определяется набором составляющих его объектов.3° Любое свойство определяет множество объектов, которые этим свойством обладают. Если х — объект, Р — свойство, Р(х) — обозначение того, что х обладает свойством Р, то через {х|Р(х)} обозначают весь класс объектов, обладающих свойством Р. Объекты, составляющие класс или множество, называют элементами класса или множества. Термин "множество" употребляется как синоним понятий совокупность, собрание, коллекция некоторых элементов. Так, можно говорить о:а) множестве пчёл в улье, б) множестве точек отрезка, в) множестве вершин квадрата или о множествах его сторон и диагоналей, г) множестве студентов в аудитории и т.д. В приведённых примерах в случаях а), в)-г) соответствующие множества состоят из определённого конечного числа предметов, такие множества называются конечными. Множество точек отрезка (пример б)) пересчитать невозможно, поэтому такие множества называются бесконечными. Множество, не содержащее ни одного элемента, называется пустым множеством. Наиболее простая форма задания множества - перечисление его элементов, например А={4, 7, 13} (множество А состоит из трёх элементов - целых чисел 4, 7, 13). Другая часто применяемая форма задания - указание свойств элементов множества, например A = {x| x^2 ≤ 4} - множество чисел х, удовлетворяющих указанному условию. Множества обычно обозначаются большими буквами А, В, С,…., а их элементы - малыми: а, в, с,… Запись а ∈ А (читается: а принадлежит А) или A ∋ a (читается: А содержит а) означает, что а есть элемент множества А. Пустое множество обозначается значком Ø. Если каждый элемент множества В является также элементом множества А, множество В называется подмножеством множества А (обозначение - B ⊆ A или A ⊇ B). Каждое множество является своим подмножеством (это самое "широкое" подмножество множества). Пустое множество является подмножеством любого множества (это самое "узкое" подмножество). Любое другое подмножество множества А содержит хотя бы один элемент множества А, но не все его элементы. Такие подмножества называются истинными, или собственными подмножествами. Для истинных подмножеств множества А применяется обозначение B ⊂ A или A ⊃ B. Если одновременно B ⊆ A и A ⊆ B, т.е каждый элемент множества В принадлежит А, и в то же время каждый элемент А принадлежит В, то А и В, очевидно, состоят из одних и тех же элементов и, следовательно, совпадают. В этом случае применяется знак равенства множеств: A = B. (Символы ∈, ∋, ⊂, ⊃, ⊆, ⊇ называются символами включения). Геометрически множества обычно изображаются как некоторые множества точек плоскости. В любой имеющей смысл задаче обычно рассматриваются подмножества некоторого "наибольшего" множества U, которое называют универсальным множеством. Так, на рис. 1 изображено универсальное множество U и два его подмножества - множества А и В, B ⊂ A. Сами картинки типа рис. 1 называются диаграммами Эйлера-Венна.

Пустое множество (в математике) — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого́ пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным (англ.) и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством. - цепочка, начинающаяся с произвольного множества, каждый последующий член которой является элементом предыдущего, всегда через конечное число шагов завершается пустым множеством (см. аксиому регулярности). Таким образом, пустое множество является «строительным кирпичиком», из которого строятся все остальные множества. В некоторых формулировках теории множеств существование пустого множества постулируется (см. аксиому пустого множества), в других — доказывается.Обозначения пустого множества - Обычно пустое множество обозначают одним из следующих символов:

Конечные и бесконечные множества. ПодмножествоДля дальнейшего изучения множеств попытаемся дать некоторую их классификацию. Прежде всего, множества можно разделить на конечные и бесконечные.Конечным множеством называется множество, состоящее из конечного числа элементов. Примерами конечных множеств могут быть множество корней алгебраического уравнения n-й степени, множество букв русского алфавита, множество персонажей романа Михаила Булгакова «Мастер и Маргарита», множество атомов Солнечной системы. Причем неважно, известно число элементов множества или нет, главное, чтобы оно существовало. В математике приходится сталкиваться и с другими – неконечными, или, как принято говорить, с бесконечными множествами. Множество называется бесконечным, если оно состоит из бесконечного числа элементов. Таковы, например, множество всех натуральных чисел, множество точек окружности, множество прямых, проходящих через точку плоскости, и т.д. К конечным множествам относится и множество, не содержащее элементов вообще. Такое множество называют пустым и обозначают Æ. Необходимость его введения вызвана тем, что, определяя множество с помощью некоторого условия, мы не всегда можем сказать заранее, содержит ли оно элементы или нет. Например, в 101-й группе может не быть отличников и тогда А={а | а – отличник 101-й группы}=Æ. Пустым множеством является и множество корней системы уравнений. Без введения пустого множества мы не могли бы, скажем, говорить о множестве корней произвольного уравнения, не убедившись предварительно, что данное уравнение имеет хотя бы один корень. Существование этого понятия сокращает и упрощает формулировки многих теорем, облегчает введение новых понятий.Если каждый элемент множества В является также и элементом множества А, то говорят, что множество В называется подмножеством множества А.Обозначатся это следующим образом: В Í А (В включено в А). Например, {2, 4} Í {2, 3, 4, 5}. Множество пешек в шахматах является подмножеством шахматных фигур, множество квадратов – подмножеством прямоугольников, множество отличников 101 группы – подмножеством студентов этой группы. Подмножество В может и совпадать с множеством А, т.е. множества А и В будут состоять из одних и тех же элементов. В этом случае множества А и В называются равными: А=В (интуитивный принцип объемности). Например, множества X={2, 3} и Y={y | } состоят из чисел 2 и 3. Значит X=Y. Если в множествах А и В отличаются хотя бы одним элементом, то А¹В.Можно заметить, что само множество А является подмножеством самого себя: А Í А. (2.1) Действительно, по определению подмножества каждый элемент множества А является элементом множества А. Это свойство множества называют рефлексивностью.Кроме того, пустое множество, по определению, считают подмножеством любого множества:Æ Í А. (2.2)В самом деле, если Æ не является подмножеством А, то в нем находится хотя бы один элемент, не содержащийся в множестве А. Но в Æ такого элемента нет, так как Æ не содержит ни одного элемента.Все множества, с которыми имеют дело в том или ином рассуждении, являются подмножествами некоторого множества I, т.е. для любого множества А А Í I.В этом случае множество I называют универсальным множеством. Например, для алгебры универсальным множеством является множество действительных чисел. Если мы рассматриваем множества точек на плоскости, то универсальным будет множество всех точек на плоскости.Таким образом, у любого множества обязательно существуют хотя бы два подмножества: пустое множество и само множество. Эти два подмножества называются несобственными подмножествами. Любое подмножество, отличное от несобственного, называется собственным подмножеством данного множества.Множество всех подмножеств множества А называется множеством-степенью множества А и обозначается P(A). Например, для А={2, 3} множество-степень P(A)={А, {2}, {3}, Æ}, для А={1,2,3} множество-степень таково: P(A)={А, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, Æ}. Название «множество-степень» исходит из того, что число всех подмножеств n-элементного множества равно . Продемонстрируем данный результат. Множество, состоящее из одного элемента а, имеет два подмножества: Æ и {a}. Множество, состоящее из двух элементов а и b, имеет уже 4 подмножества: те же Æ и {a} и еще {b}, {a, b}. Добавим третий элемент с. Множество {a, b, c} кроме рассмотренных выше 4 подмножеств Æ, {a}, {b}, {a, b} имеет еще 4 подмножества {c}, {a, c}, {с, b}, {a, b, c}.Таким образом, ясно, что каждый раз прибавление еще одного элемента ведет к удвоению числа подмножеств. И множество, состоящее из n-элементов, имеет подмножеств.Кроме свойств (2.1) и (2.2) выделяют следующие свойства отношения включения: · если АÍВ и ВÍС, то АÍС (транзитивность);· если АÍВ и ВÍА, то А=В. (2.3)Для выражения (2.3) верно и обратное ему: если А=В, то АÍВ и ВÍА. Эти выражения непосредственно вытекают из определений подмножества и равенства множеств.Множество А называется истинным подмножеством множества В, если АВ и А≠В. В этом случае записывают:АÌВ.Так, {2, 4} Ì {2, 3, 4, 5}. Множество пешек в шахматах также будет истинным подмножеством шахматных фигур, а вот множество отличников 101-й группы может, чисто теоретически, совпадать с множеством студентов 101-й группы. Для истинных подмножеств также выполняется свойство транзитивности: если АВ и ВС, то АС.

Операции над множествами Объединением множеств A и B называется множество элементов, принадлежащих по крайней мере одному из данных множеств (т. е. либо A, либо B, либо одновременно и A и B). Обозначают и читают "объединение A и B".Пересечением множеств A и B называется множество элементов, принадлежащих одновременно и A и B. Обозначают и читают "пересечение A и B".Разностью множеств A и B называется множество элементов, принадлежащих A и не принадлежащих B. Обозначают A\B и читают "разность A и B".Пример 1. Пусть A есть отрезок [1, 3], B - отрезок [2, 4]; тогда объединением будет отрезок [1, 4], пересечением - отрезок [2, 3], разностью A\B - полуинтервал [1, 2), B\A - полуинтервал (3, 4]. Пример 2. Пусть A есть множество прямоугольников, B - множество всех ромбов на плоскости. Тогда есть множество всех квадратов, A\B - множество прямоугольников с неравными сторонами, B\A - множество всех ромбов с неравными углами .Операции объединения и пересечения множеств обладают многими свойствами сложения и умножения чисел, например переместительным, сочетательным и распределительным свойствами. Понятия объединения и пересечения множеств дословно переносятся на случай более двух множеств и даже на случай любого конечного или бесконечного множества множеств. Для удобства будем называть системами такие множества, элементами которых служат другие множества. Тогда объединением множеств некоторой системы называется множество, состоящее из элементов, принадлежащих по крайней мере одному множеству данной системы. Пересечением множеств некоторой системы называется множество, состоящее из элементов, входящих во все множества данной системы. Применяются следующие обозначения. В случае конечной системы множеств A1, A2, ..., An объединение S и пересечение D обозначаются:

2. Перестановки элемента множества. Число постановок Рn . Примеры.

В комбинаторике перестано́вка — это упорядоченный набор чисел обычно трактуемый как биекция на множестве ,которая числу i ставит соответствие i-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.

В теории групп под перестановкой произвольного множества подразумевается биекция этого множества на себя. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово подстановка. (Другие авторы подстановкой называют наглядный способ записи перестановки.)

Число всех перестановок порядка равно числу размещений из n по n, то есть факториалу:

Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка n образует группу, которую называют симметрической и обычно обозначают

Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элементсопоставляется с перестановкой, задаваемой тождествомгде g — произвольный элемент группы G, а — групповая операция.

Комбинаторика - это раздел математики, в котором изучаются вопросы о том, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов. Основы комбинаторики очень важны для оценки вероятностей случайных событий, т.к. именно они позволяют подсчитать принципиальновозможное количество различных вариантов развития событий.

Основная формула комбинаторики

Пусть имеется k групп элементов, причем i-я группа состоит из ni элементов. Выберем по одному элементу из каждой группы. Тогда общее число N способов, которыми можно произвести такой выбор, определяется соотношением N=n1*n2*n3*...*nk.

Пример 1. Поясним это правило на простом примере. Пусть имеется две группы элементов, причем первая группа состоит из n1 элементов, а вторая - из n2 элементов. Сколько различных пар элементов можно составить из этих двух групп, таким образом, чтобы в паре было по одному элементу от каждой группы? Допустим, мы взяли первый элемент из первой группы и, не меняя его, перебрали все возможные пары, меняя только элементы из второй группы. Таких пар для этого элемента можно составить n2. Затем мы берем второй элемент из первой группы и также составляем для него все возможные пары. Таких пар тоже будет n2. Так как в первой группе всего n1 элемент, всего возможных вариантов будет n1*n2.

Пример 2. Сколько трехзначных четных чисел можно составить из цифр 0, 1, 2, 3, 4, 5, 6, если цифры могут повторяться?

Решение: n1=6 (т.к. в качестве первой цифры можно взять любую цифру из 1, 2, 3, 4, 5, 6), n2=7 (т.к. в качестве второй цифры можно взять любую цифру из 0, 1, 2, 3, 4, 5, 6), n3=4 (т.к. в качестве третьей цифры можно взять любую цифру из 0, 2, 4, 6).

Итак, N=n1*n2*n3=6*7*4=168.

В том случае, когда все группы состоят из одинакового числа элементов, т.е. n1=n2=...nk=n можно считать, что каждый выбор производится из одной и той же группы, причем элемент после выбора снова возвращается в группу. Тогда число всех способов выбора равно nk.Такой способ выбора носит название выборки с возвращением.

Пример 3. Сколько всех четырехзначных чисел можно составить из цифр 1, 5, 6, 7, 8?

Решение. Для каждого разряда четырехзначного числа имеется пять возможностей, значит N=5*5*5*5=54=625.

Рассмотрим множество, состоящие из n элементов. Это множество будем называть генеральной совокупностью.

Определение 1. Размещением из n элементов по m называется любой упорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 4. Различными размещениями из трех элементов {1, 2, 3} по два будут наборы (1, 2), (2, 1), (1, 3), (3, 1), (2, 3),(3, 2). Размещения могут отличаться друг от друга как элементами, так и их порядком.

Число размещений обозначается Anm и вычисляется по формуле:

Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1.

Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные?

Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет:

Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов.

Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}.

Число сочетаний обозначается Cnm и вычисляется по формуле:

Пример 7. Сколькими способами читатель может выбрать две книжки из шести имеющихся?

Решение: Число способов равно числу сочетаний из шести книжек по две, т.е. равно:

Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов.

Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2).

Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!.

Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд?

Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг.

Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно.

Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов).

Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны.

И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере.

Пример. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек?

Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5.

Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5.

Число перестановок - число различных способов, которыми может быть упорядочено данное множество, состоящее из n элементов.

Нахождение числа перестановок из n элементов.

Pn (P – первая буква французского слова permutation – перестановка). Читается: “Число перестановок из эн элементов” или “Пэ из эн”.

В задании 1 было показано P4 = 4*3*2*1 = 1*2*3*4 (по переместительному свойству умножения).

Pn=1*2*3*…*n (1)

т.о., число перестановок из n элементов равно произведению всех натуральных чисел от 1 до n.

При использовании символа n! формула (1) принимает вид Pn= n!

(Учащимся: правило нахождения перестановок из n элементов записать в тетрадь словами и формулой, выучить, рассказать соседу по парте).

Пример 1. В расписании 7 класса на четверг должно быть 6 предметов: русский язык, литература, алгебра, география, физика, физкультура. Сколькими способами можно составить расписание на этот день?

Решение. Число способов, которыми можно составить расписание, равно числу перестановок из шести элементов: P6=6!=1*2*3*4*5*6=720.

Пример 2. Сколькими способами можно составить расписание из тех же 6 предметов, если требуется, чтобы урок физкультуры был последним?

Решение. У урока физкультуры фиксированное место, поэтому расписания отличаются порядком остальных 5 предметов. Значит, число таких расписаний равно числу перестановок из 5 элементов: P5=5!= 120.

Пример 3. Сколькими способами из тех же 6 предметов можно составить такое расписание, в котором русский язык и литература стоят рядом?

Решение. Будем рассматривать русский язык и литературу как один предмет, тогда всего предметов будет пять. Число способов, которыми можно составить расписание из 5 предметов, равно P5=5!. Но в каждой из этих перестановок русский язык и литература могут меняться местами. Поэтому искомое число расписаний вдвое больше. Оно равно 5!*2=240.

1) в задачах на перестановки используются все элементы данного набора элементов;

2) две перестановки одного набора элементов отличаются друг от друга только порядком элементов).

Задание 4 Сколькими способами можно выписать в колонку фамилии 30 учеников? Решение. P30 = 30!

Задание 5 Сколько различных 5-значных чисел, все цифры которых различны можно записать с помощью цифр 4, 5, 6, 7, 8? Решение. Задача сводится к подсчету числа перестановок из 5 элементов. P5 = 1*2*3*4*5 = 120. Ответ: 120 различных чисел.

Задание 6 Сколькими способами можно расставить на полке 8 книг, если среди них 2 книги одного автора, которые при любых перестановках должны стоять рядом? Решение: первоначально будем считать 2 книги одного автора единой книгой. Тогда количество способов расстановки условных семи книг на полке будет равно числу перестановок из 7 элементов: P7 = 1*2*3*4*5*6*7 = 5040. Но в каждой такой перестановке книги одного автора можно менять местами, потому общее число способов расстановки книг на полке будет в 2 раза больше, т.е. 5040 * 2 = 10080. Ответ: 10080 способов.(стр. 47 МШ - 3 - 2003).

Задание 7 У Атоса, Портоса и Арамиса на всех имеется одна шпага, один кинжал и один пистолет. Сколько у них способов распределить оружие так, чтобы все были вооружены? Решение. Мушкетёров выстроим в шеренгу и отдадим каждому один из видов оружия. Тогда из шпаги, кинжала и пистолета необходимо составить различные перестановки, т. е. P3 = 3! = 1 = 6.

Задание 8. Четыре лектора должны прочитать по одной лекции. Сколько имеется вариантов составления расписания? Решение. P4 = 4! = = 24

Задание 9. Капитан Жеглов рассматривает фотографии. Всего их у него 25. Сколько существует различных последовательностей их рассматривания? Решение. P25 = 25!

Задание 10 У мамы есть один апельсин, одна груша, одно яблоко и один банан. Она хочет раздать их четверым детям так, чтобы каждому достался какой-нибудь фрукт. Сколько имеется вариантов это сделать? Решение. P4 = 4!=24.

3. Размещение элементов множества. Число размещений Аn. Примеры.

Размещением из n элементов множества Х по k элементам назовем любой упорядоченный набор элементов множества Х.

Если выбор элементов множества У из Х происходит с возвращением, т.е. каждый элемент множества Х может быть выбран несколько раз, то число размещений из n по k находится по формуле (размещения с повторениями). Если же выбор делается без возвращения, т.е. каждый элемент множества Х можно выбирать только один раз, то количество размещений из n по k обозначается и определяется равенством

Частный случай размещения при n=k называется перестановкой из n элементов. Число всех перестановок из n элементов равно

Пусть теперь из множества Х выбирается неупорядоченное подмножество У (порядок элементов в подмножестве не имеет значения). Сочетаниями из n элементов по k называются подмножества из k элементов, отличающиеся друг от друга хотя бы одним элементом. Общее число всех сочетаний из n по k обозначается и равно

При решении задач комбинаторики используют следующие правила: Правило суммы. Если некоторый объект А может быть выбран из совокупности объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из совокупности объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана m*n способами.

Размещение из n элементов по r есть упорядоченный набор, состоящий из r различных элементов, взятых из n-элементного множества M.

Обозначим через ArM множество всех размещений из М по r и через Arn – число всех размещений из n элементов по r.

Пример: M = (а,b,с); A1M = {(а), (b). (с)}; A2M = {(а,b),(а,с), (b,с),(b,а),(с,а),(с,b)}; A13 = |A1M| = 3; A23 = | A2M | = 6.

В размещениях, перестановках, сочетаниях элементов некоторого n-элементного множества могут допускаться повторы элементов. Будем называть их размещениями, перестановками, сочетаниями с повторами. Обозначим через A’rM, P’rM, C’rM – множества всех размещений, перестановок, сочетаний множества М с повторами, а через A’rn, P’rn, C’rn- их числа соответственно. Иногда чтобы подчеркнуть число элементов конфигурации, говорят: r-размещение, r-сочетание, r-перестановка. Например, если M={a,b,c}, то C’2M = {(а,а),(b,b),(с,с),(а,b),(а,с),(b,с)}; C’23 = |C’2M| = 6; A’2M =

{(а,а),(b,b),(с,с),(а,b),(а,с),(b,с),(b,а),(с,а),(с,b)}; A’23 = 9.

Размещения, перестановки, сочетания, составленные из элементов некоторого множества M, называются комбинаторными конфигурациями из множества М. Всякая конфигурация (а1, а2,…,аr) множества М лежит в декартовом произведении MхMх…хM, состоящем из r сомножителей. Мощности множеств комбинаторных конфигураций называются комбинаторными числами.

Amn= m·(m−1)·(m−2) …(m−(n−1)) - Общее число размещений из m элементов в группах по n обозначается Amn. Это число равно произведению n последовательных целых чисел, из которых наибольшее равно m.

4. Сочетание (подмножества) элементов множества. Число сочетаний . Примеры.

В комбинаторике сочетанием из n по k называется набор k элементов, выбранных из данного множества, содержащего n различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-хэлементные сочетания, подмножества,k=3 ) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} (n=6) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

В общем случае число, показывающее, сколькими способами можно выбрать k элементов из множества, содержащего n различных элементов, стоит на пересечении k-й диагонали и n-й строки треугольника Паскаля.

Комбинаторные формулы

Пусть имеется множество, состоящее из n элементов. Обозначим его . Перестановкой из n элементов называется заданный порядок во множестве .

Примеры перестановок:1)распределение n различных должностей среди n человек;2)расположение n различных предметов в одном ряду.

Сколько различных перестановок можно образовать во множестве ? Число перестановок обозначается P_n (читается “Р из n”).

Чтобы вывести формулу числа перестановок, представим себе n ячеек, пронумерованных числами 1,2,...n. Все перестановки будем образовывать, располагая элементы U_n в этих ячейках. В первую ячейку можно занести любой из n элементов (иначе: первую ячейку можно заполнить n различными способами). Заполнив первую ячейку, можно найти n–1 вариантов заполнения второй ячейки. Таким образом, существует n(n–1) вариантов заполнения двух первых ячеек. При заполнении первых двух ячеек можно найти n–2 варианта заполнения третьей ячейки, откуда получается, что три ячейки можно заполнить n(n-1)(n-2) способами. Продолжая этот процесс, получим, что число способов заполнения n ячеек равно . ОтсюдаP_n = n(n – 1)(n – 2)...321

Число n(n – 1)(n – 2)...321, то есть произведение всех натуральных чисел от 1 до n, называется "n-факториал" и обозначается n! Отсюда P_n =n!

По определению считается: 1!=1; 0!=1. Пример. Сколько существует вариантов замещения 5-ти различных вакантных должностей 5-ю кандидатами? . Размещениями из n элементов по k элементов будем называть упорядоченные подмножества, состоящие из k элементов множества (множества, состоящего из n элементов). Число размещений из n элементов по k элементов обозначается (читается "А из n по k").

Одно размещение из n элементов по k элементов может отличаться от другого как набором элементов, так и порядком их расположения.

Примеры задач, приводящих к необходимости подсчета числа размещений1) Сколькими способами можно выбрать из 15 человек 5 кандидатов и назначить их на 5 различных должностей?2) Сколькими способами можно из 20 книг отобрать 12 и расставить их в ряд на полке?

В задачах о размещениях полагается k < n. В случае, если k = n, то легко получить Для подсчетаиспользуем тот же метод, что использовался для подсчетаP_n, только здесь возьмем лишь k ячеек. Первую ячейку можно заполнить n способами, вторую, при заполненной первой, можно заполнить n–1 способами. Таким образом, существует п(п – 1) вариантов заполнения первых двух ячеек. Можно продолжать этот процесс до заполнения последней k–й ячейки. Эту ячейку при заполненных первых k – 1 ячейках можно заполнить n–(k–1) (или n–k+1) способами. Таким образом, все k ячеек заполняются числом способов, равным

Отсюда получаем:

Пример. Сколько существует различных вариантов выбора 4-х кандидатур из 9-ти специалистов для поездки в 4 различных страны?

Сочетаниями из n элементов по k элементов называются подмножества, состоящие из k элементов множества (множества, состоящего из n элементов).

Одно сочетание от другого отличается только составом выбранных элементов (но не порядком их расположения, как у размещений).

Число сочетаний из n элементов по k элементов обозначается (читается "C из n по k").

Примеры задач, приводящих к подсчету числа сочетаний:1) Сколько существует вариантов выбора 6-ти человек из 15 кандидатов для назначения на работу в одинаковых должностях?2)Сколькими способами можно из 20книг отобрать12 книг?

Выведем формулу для подсчета числа сочетаний. Пусть имеется множество и нужно образовать упорядоченное подмножество множества , содержащееk элементов (то есть образовать размещение). Делаем это так:

1) выделим какие-либо k элементов из n элементов множества Это, согласно сказанному выше, можно сделать способами;

2) упорядочим выделенные k элементов, что можно сделать способами. Всего можно получитьвариантов (упорядоченных подмножеств), откуда следует:, то есть

Пример: 6 человек из 15 можно выбрать числом способов, равным

Несложно понять, что осуществить выбор подмножества из т элементов множества, насчитывающего п элементов, можно, выбрав п – т элементов, которые не войдут в интересующее нас подмножество.Отсюда следует свойство числа сочетаний Эту формулу можно доказать, используя формулу (1). Задачи на подсчет числа подмножеств конечного множества называются комбинаторными. Рассмотрим некоторые комбинаторные задачи.

1.Из семи заводов организация должна выбрать три для размещения трех различных заказов. Сколькими способами можно разместить заказы? Так как из условия ясно, что каждый завод может либо получить один заказ, либо не получить ни одного, и что выбрав три завода, можно по-разному разместить среди них заказы, здесь нужно считать число размещений

2.Если из текста задачи 1 убрать условие различия трех заказов, сохранив все остальные условия, получим другую задачу. Теперь способ размещения заказов определяется только выбором тройки заводов, так как все эти заводы получат одинаковые заказы, и число вариантов определяется как число сочетаний.

3.Имеются 7 заводов. Сколькими способами организация может разместить на них три различных производственных заказа? (Заказ нельзя дробить, то есть распределять его на нескольких заводах).

В отличие от условия первой задачи, здесь организация может отдать все три заказа первому заводу или, например, отдать два заказа второму заводу, а один - седьмому.

Задача решается так. Первый заказ может быть помещен семью различными способами (на первом заводе, на втором и т.д.). Поместив первый заказ, имеем семь вариантов помещения второго (иначе, каждый способ помещения первого заказа может сопровождаться семью способами помещения второго). Таким образом, существует 77=49 способов размещения первых двух заказов. Разместив их каким-либо образом, можем найти 7 вариантов помещения третьего (иначе, каждый способ размещения первых двух заказов может сопровождаться семью различными способами помещения третьего заказа). Следовательно, существуют 497=7³ способов размещения трех заказов. (Если бы заказов было n, то получилось бы 7ⁿ способов размещения).

4.Как решать задачу 3, если в ее тексте вместо слов "различных производственных заказа" поставить "одинаковых производственных заказа"? Это трудная задача. Ниже приводится аналогичная задача– Задача V с решением.

5.Добавим к условию задачи 1 одну фразу: организация также должна распределить три различных заказа на изготовление деревянных перекрытий среди 4-х лесопилок. Сколькими способами могут быть распределены все заказы?

Каждый из способов распределения заказов на заводах может сопровождатьсяспособами размещения заказов на лесопилках. Общее число возможных способов размещения всех заказов будет равно

6. Риэлтерская фирма предлагает на продажу 5 больших квартир и 4 малогабаритных квартиры. Банк намеревается купить 4квартиры, причём среди них не должно быть более двух малогабаритных. Сколько вариантов выбора имеет банк? Банк может купить 4 большие квартиры. У него есть возможность выбрать 4 из 5-ти предлагаемых квартир, и число вариантов здесь равно . Если банк решит купить три большие квартиры и одну малогабаритную, то число вариантов выбора у него будет равно. Если будет принято решение купить две малогабаритных квартиры и две больших квартиры, то число вариантов будет равным. Таким образом, у банка есть 105 вариантов выбора.

5. Матрица. Виды матриц. Сложение и вычитание матриц, умножение на число, транспонирование. Примеры.

Матрицей называется прямоугольная таблица чисел. Так, 230

104 есть матрица с двумя строками и тремя столбцами. Обозначим ее A. Обычно элементы матрицы обозначаются теми же буквами, что и матрица, но строчными: A = (ai j). В этой матрице всего 6 элементов: a11 = 2, a12 = 3, a13 = 0, a21 = 1, a22 = 0, a23 = 4 (надо читать эти элементы так: a11 — а-один-один, a12 — а-один-два и т.д.). Число строк и число столбцов в матрице называются ее размерами, причем число строк называют первым. Итак, A есть матрица размером 2 × 3. Две матрицы считаются равными (одинаковыми) тогда и только тогда, если у них совпадают их размеры, т.е. число строк и число столбцов, и совпадают сами строки и столбцы. Пусть, например,A = (ai j) есть матрица m × n и B = (bi j) есть матрица k × s; тогда A = B, если и только если k = m, s = n и ai j = bi j для любых i = 1, ..., m и j = 1, ..., n. Таким образом, бессмысленно говорить о равенстве матриц при несовпадении их размеров. Если число строк равно числу столбцов, то матрица называется квадратной. В квадратной матрице элементы ai i образуют главную диагональ матрицы. Если в квадратной матрице все элементы — нули и только на главной диагонали все элементы есть единицы, то такая матрица называется единичной. Так,

E3 = 100

010

001 есть единичная матрица размера 3. В каждой размерности есть своя единичная матрица.Рассмотрим матрицу A размерами m × n. Каждую ее строку мож- но считать вектором-строкой размерности n и каждый столбец — вектором-столбцом размерности m. Обозначим i-ю строку-вектор a i , j-й столбец-вектор Aj, тогда матрицу A можно представить упо- рядоченным набором векторов-строк:

A = a1

.

.

.

a m или упорядоченным набором векторов-столбцов: A = (A1, ..., An) . Заметим, что векторы можно рассматривать как частный случай матриц. Так, вектор-строка может рассматриваться как матрица содной строкой; аналогично вектор-столбец — как матрица с одним столбцом.

Виды матриц

1. Прямоугольные: m и n - произвольные положительные целые числа

2. Квадратные: m=n

3. Матрица строка: m=1. Например, (1 3 5 7 ) - во многих практических задачах такая матрица называется вектором

4. Матрица столбец: n=1. Например

5. Диагональная матрица: m=n и aij=0, если i≠j. Например

6. Единичная матрица: m=n и

7. Нулевая матрица: aij=0, i=1,2,...,m

j=1,2,...,n

8. Треугольная матрица: все элементы ниже главной диагонали равны 0.

Пример.

9. Симме трическая матрица: m=n и aij=aji (т.е. на симметричных относительно главной диагонали местах стоят равные элементы), а следовательно A'=AНапример,

10. Кососимметрическая матрица: m=n и aij=-aji (т.е. на симметричных относительно главной диагонали местах стоят противоположные элементы). Следовательно, на главной диагонали стоят нули (т.к. при i=j имеем aii=-aii) Пример.

11. Эрмитова матрица: m=n и aii=-ãii (ãji - комплексно - сопряженное к aji, т.е. если A=3+2i, то комплексно - сопряженное Ã=3-2i) Пример

Сложение матриц - поэлементная операция

Вычитание матриц - поэлементная операция

Умножение матрицы на число

В результате умножения матрицы на число получается матрица такой же размерности, что и исходная, каждый элемент которой является результатом произведения соответствующего элемента исходной матрицы на число.

Мы получим одинаковый результат, умножая число на матрицу, или матрицу на число. Из определения следует, что общий множитель всех элементов матрицы можно выносить за знак матрицы

Транспонирование матриц – переход от матрицы А к матрице, в которой строки и столбцы поменялись местами с сохранением порядка.

Пример 1. Составить транспонированную матрицу, полученную из А:

Решение: Поменяем местами строки и столбцы, сохраняя порядок:

Операция умножения матриц

Определение: Произведением матриц называется матрица, элементы которой могут быть вычислены по следующим формулам:

A×B = C;

Из приведенного определения видно, что операция умножения матриц определена только для матриц, число столбцов первой из которых равно числу строк второй.

Свойства операции умножения матриц.

1)Умножение матриц не коммутативно, т.е. АВ ¹ ВА даже если определены оба произведения. Однако, если для каких – либо матриц соотношение АВ=ВА выполняется, то такие матрицы называются перестановочными.

Самым характерным примером может служить единичная матрица, которая является перестановочной с любой другой матрицей того же размера.

Перестановочными могут быть только квадратные матрицы одного и того же порядка. А×Е = Е×А = А

Очевидно, что для любых матриц выполняются следующее свойство: A×O = O; O×A = O, где О – нулевая матрица.

2) Операция перемножения матриц ассоциативна, т.е. если определены произведения АВ и (АВ)С, то определены ВС и А(ВС), и выполняется равенство:(АВ)С=А(ВС).

3) Операция умножения матриц дистрибутивна по отношению к сложению, т.е. если имеют смысл выражения А(В+С) и (А+В)С, то соответственно: А(В + С) = АВ + АС (А + В)С = АС + ВС.

4) Если произведение АВ определено, то для любого числа a верно соотношение: a(AB) = (aA)B = A(aB).

5) Если определено произведение АВ , то определено произведение ВТАТ и выполняется равенство: (АВ)Т = ВТАТ, где

индексом Т обозначается транспонированная матрица.

6) Заметим также, что для любых квадратных матриц det (AB) = detA×detB.

6. Определители второго и третьего порядков. Примеры.

Определитель первого порядка равен тому единственному элементу, из которого состоит соответствующая матрица.

Определитель второго порядка вычислим, например, по элементам первой строки

Запишем разложение данного определителя по элементам второй строки

Полученный результат совпадает с результатом вычисления определителя по первой строке. Этот же результат получится и при разложении по любому из столбцов. Рекомендуем это проверить самостоятельно.

Из сказанного можно заключить, что определитель второго порядка равен произведению элементов, стоящих на главной диагонали, минус произведение элементов, стоящих на побочной диагонали.

Пример.

Найдем определитель третьего порядка, раскладывая его по элементам, например, третьего столбца

Пример.

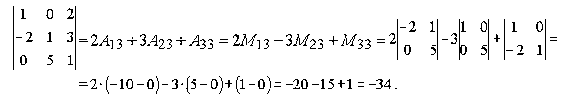
Таким образом, вычисление определителя третьего порядка сводится к вычислению определителей второго порядка.

Получается, что определитель n - го порядка мы найдем через определители (n -1) - го порядка.

7. Вероятность. Классическая формула вычисления вероятности. Статистическая вероятность. Примеры с игральными костями и монетами.

Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое называют классическим. Далее укажем слабые стороны этого определения и приведем другие определения, позволяющие преодолеть недостатки классического определения.

Рассмотрим пример. Пусть в урне содержится 6 одинаковых, тщательно перемешанных шаров, причем 2 из них - красные, 3 - синие и 1 - белый. Очевидно, возможность вынуть наудачу из урны цветной (т. е. красный или синий) шар больше, чем возможность извлечь белый шар. Можно ли охарактеризовать эту возможность числом? Оказывается, можно. Это число и называют вероятностью события (появления цветного шара). Таким образом, вероятность есть число, характеризующее степень возможности появления события.

Поставим перед собой задачу дать количественную оценку возможности того, что взятый наудачу шар цветной. Появление цветного шара будем рассматривать в качестве события А. Каждый из возможных результатов испытания (испытание состоит в извлечении шара из урны) назовем элементарным исходом (элементарным событием). Элементарные исходы обозначим через w1, w2, w3 и т.д. В нашем примере возможны следующие 6 элементарных исходов: w1 - появился белый шар; w2, w3 - появился красный шар; w4, w5, w6 - появился синий шар. Легко видеть, что эти исходы образуют полную группу попарно несовместных событий (обязательно появится только один шар) и они равновозможны (шар вынимают наудачу, шары одинаковы и тщательно перемешаны).

Те элементарные исходы, в которых интересующее нас событие наступает, назовем благоприятствующими этому событию. В нашем примере благоприятствуют событию A (появлению цветного шара) следующие 5 исходов: w2, w3, w4, w5, w6.

Таким образом, событие А наблюдается, если в испытании наступает один, безразлично какой, из элементарных исходов, благоприятствующих A; в нашем примере А наблюдается, если наступит w2, или w3, или w4, или w5, или w6. В этом смысле событие А подразделяется на несколько элементарных событий (w2, w3, w4, w5, w6); элементарное же событие не подразделяется на другие события. В этом состоит различие между событием А и элементарным событием (элементарным исходом).

Отношение числа благоприятствующих событию А элементарных исходов к их общему числу называют вероятностью события А и обозначают через Р (А). В рассматриваемом примере всего элементарных исходов 6; из них 5 благоприятствуют событию А. Следовательно, вероятность того, что взятый шар окажется цветным, равна Р (A) = 5 / 6. Это число и дает ту количественную оценку степени возможности появления цветного шара, которую мы хотели найти. Дадим теперь определение вероятности.

Вероятностью события А называют отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Итак, вероятность события А определяется формулой

Р (A) = m / n,где m - число элементарных исходов, благоприятствующих A; n - число всех возможных элементарных исходов испытания.

Здесь предполагается, что элементарные исходы несовместны, равновозможны и образуют полную группу. Из определения вероятности вытекают следующие ее свойства:

С в о й с т в о 1. Вероятность достоверного события равна единице.

Действительно, если событие достоверно, то каждый элементарный исход испытания благоприятствует событию. В этом случае m = n, следовательно,

Р (A) = m / n = n / n = 1.

С в о й с т в о 2. Вероятность невозможного события равна нулю.

Действительно, если событие невозможно, то ни один из элементарных исходов испытания не благоприятствует событию. В этом случае m = 0, следовательно,

Р (А) = m / n = 0 / n = 0.

С в о й с т в о 3. Вероятность случайного события есть положительное число, заключенное между нулем и единицей.

Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания. В этом случае 0 < m < n, значит, 0 < m / n < 1, следовательно, 0 < Р (А) < 1

Итак, вероятность любого события удовлетворяет двойному неравенству 0 <= Р (A) < 1.

Далее приведены теоремы, которые позволяют по известным вероятностям одних событий находить вероятности других событий.

З а м е ч а н и е. Современные строгие курсы теории вероятностей построены на теоретико-множественной основе. Ограничимся изложением на языке теории множеств тех понятий, которые рассмотрены выше.

Пусть в результате испытания наступает одно и только одно из событий wi, (i = 1, 2, ..., n). События wi, называют элементарными событиями (элементарными исходами). Уже отсюда следует, что элементарные события попарно несовместны. Множество всех элементарных событий, которые могут появиться в испытании, называют пространством элементарных событий W, а сами элементарные события - точками пространства W.

Событие А отождествляют с подмножеством (пространства W), элементы которого есть элементарные исходы, благоприятствующие А; событие В есть подмножество W, элементы которого есть исходы, благоприятствующие В, и т.д. Таким образом, множество всех событий, которые могут наступить в испытании, есть множество всех подмножеств W. Само W наступает при любом исходе испытания, поэтому W - достоверное событие; пустое подмножество пространства W - невозможное событие (оно не наступает ни при каком исходе испытания).

Заметим, что элементарные события выделяются из числа всех событий тем, что каждое из них содержит только один элемент W.

Каждому элементарному исходу wi, ставят в соответствие положительное число pi - вероятность этого исхода, причем

По определению, вероятность Р(А) события А равна сумме вероятностей элементарных исходов, благоприятствующих А. Отсюда легко получить, что вероятность события достоверного равна единице, невозможного - нулю, произвольного - заключена между нулем и единицей.

Рассмотрим важный частный случай, когда все исходы равновозможны. Число исходов равно n, сумма вероятностей всех исходов равна единице; следовательно, вероятность каждого исхода равна 1 / n. Пусть событию А благоприятствует m исходов. Вероятность события А равна сумме вероятностей исходов, благоприятствующих А: Р (А) = 1 / n + 1 / n + .. + 1 / n.

Учитывая, что число слагаемых равно m, имеем Р (А) = m / n.

Получено классическое определение вероятности.

Построение логически полноценной теории вероятностей основано на аксиоматическом определении случайного события и его вероятности. В системе аксиом, предложенной А. Н. Колмогоровым, неопре-деляемыми понятиями являются элементарное событие и вероятность. Приведем аксиомы, определяющие вероятность: 1. Каждому событию А поставлено в соответствие неотрицательное действительное число Р (А). Это число называется вероятностью события А.

2. Вероятность достоверного события равна единице: P(W) = l.

3. Вероятность наступления хотя бы одного из попарно несовместных событий равна сумме вероятностей этих событий.

Исходя из этих аксиом, свойства вероятностей и зависимости между ними выводят в качестве теорем.

Классическая формула для определения вероятности наступления случайного события X выглядит следующим образом:

где Nx — количество вариантов возможного наступления случайного события х;

N— общее количество возможных исходов. Пример. Бросая игральную кость, мы можем получить шесть возможных исходов — выпадение одной из шести граней игральной кости: 1,2,3, 4, 5 или 6. Таким образом, можно определить вероятность выпадения одной из граней, например 3:

Таким образом, вероятность выпадения одной из граней игральной кости (в нашем примере 3) составляет 16.67%.

Можно также определить вероятность выпадения одной из двух граней (например, 2 или 3). В этом случае используется правило сложения вероятностей, а вероятность рассчитывается следующим образом: Р(х8; By) = Р{х) + Р{у) = 0.1667 + 0.1667 = 0.3333 или 33.33%, где Р(х) — вероятность наступления случайного события х (в нашем примере 2);

Р(у) — вероятность наступления случайного события у (3).

Таким образом, вероятность выпадения грани с цифрой 2 или 3 равна 33.33%.

Правило сложения вероятностей используется для зависимых событий, когда одно случайное событие исключает наступление другого случайного события.

Если необходимо найти вероятность одновременного наступления двух и более случайных событий, используется правило умножения вероятностей. При этом все события должны быть независимы друг от друга.

Пример. В результате одновременного броска двух игральных костей мы можем получить 36 различных комбинаций: 1 — 1,1—2,1—3,1—4,1— 5, 1—6, 2—1, 2—2, 2—3 и т.д. Для определения вероятности того, что в результате подбрасывания мы получим на гранях обеих игральных костей по 1, используем правило умножения вероятностей:

Р(х8; 87) = Р{х)хР{у) = 0.1667x0.1667 = 0.0278 или 2.78%

Таким образом, вероятность одновременного выпадения на двух игральных костях граней с цифрой 1 равна 2.78%.

Статистическая вероятность

При статистическом определении в качестве вероятности события принимают его относительную частоту.

где m - число испытаний, в которых событие A наступило, n - общее число произведённых испытаний.

Пример 2.1

В некотором районе зарегистрировано рождение с начала года 1248 младенцев, из них 645 мальчиков. Какова вероятность рождения мальчика в данном районе?

Решение

За вероятность принимаем относительную частоту рождения мальчиков. W = 645/1248 ≈ 0,517

Задача 1.

Игральная кость подбрасывается два раза. Какова вероятность того, что хотябы один раз появляется шестерка?

РЕШЕНИЕ

Результат двукратного подбрасывания кости можно описать множеством U строк u = u1u2 длины 2, составленных из чисел 1, 2, 3, 4, 5, 6. Число таких строк равно 62 = 36.Симметричность кости позволяет использовать модель Лапласа для n = 36 равновероятных исходов. Задача сводится к вычислению вероятности Р(С) события С, составленного из строк u = u1u2 для которых u1 = 6 или u2 = 6:

С = {61, 62, 63, 64, 65, 66,16, 26, 36, 46, 56}.

1. Имеем: P(C) = n(C)/n(U) = 11/36.

2. Дополнение А = С` события С состоит из строк u = u1u2 для которых u1 ≠ 6 или u2 ≠ 6. Число таких строк равно 52 = 25. Поэтому Р(С`) = Р(А) = 52/62 = (5/6)2.

По правилу дополнения Р(С) = Р(А’) = 1 - (5/6)2 = 11/36.

3. Событие С можно представить в виде объединения событий А = {61,62,63,64,65,66} и В = {16,26,36,46,56,66}, описывающих появление шестерки соответственно при первом и втором подбрасываниях.

Имеем: P(А) = 6/36, Р(B) = 6/36, Р(АВ) = Р ({66}) = 1/36.

По правилу объединения, P(С) = Р(A U В) = Р(А) + Р(В) - Р(АВ) = 6/36 + 6/36 - 1/36 = 11/36.

В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков. Результат округлите до сотых.

Итак, вероятность события - это отношение благоприятных исходов к общему количеству исходов. То есть, для нашего примера: чтобы найти вероятность того, что в сумме выпадет 8 очков нужно разделить количество исходов при которых выпадает 8 очков на общее количество исходов. Всего возможно 36 вариантов исходов:

Первая игр. кость	Вторая игр. кость	Сумма очков
1 1 1 1 1 1 2 2 2 2 2 2 3 3 3 3 3 3	1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6	2 3 4 5 6 7 3 4 5 6 7 8 4 5 6 7 8 9

Первая кость	Вторая кость	Сумма очков
4 4 4 4 4 4 5 5 5 5 5 5 6 6 6 6 6 6	1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6	5 6 7 8 9 10 6 7 8 9 10 11 7 8 9 10 11 12

Благоприятные исходов 5 (первое число количество очков первой игральной кости, второе число количество очков второй игральной кости) : 2 и 6, 3 и 5, 4 и 4, 5 и 3, 6 и 2.

Таким образом, вероятность, что в сумме выпадет 8 очков равна:P8=5/36≈0,14

Ответ к задаче, вероятность равна 0,14 или 14%.

Пример 2: В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.

Алгоритм решения задачи аналогичен алгоритму решению предыдущей задачи. Нужно определить сколько всего вариантов и сколько из них благоприятные варианты. Перечислим все варианты (О-выпал орел, Р-выпала решка):

А Б С Д

Первый бросок О Р О Р

Второй бросок О Р Р О

Итак, всего возможно 4 варианта. Благоприятных вариантов 2 - вариант С и Д (только в них Орел выпадает ровно один раз). Следовательно, вероятность того, что орел выпадет ровно один раз равна:

РО=2/4=0,5

Ответ к задаче, вероятность равна 0,5 или 50%.

7. Геометрическая вероятность(линейный плоский объемный случаи). Примеры.

Геометрическая вероятность

Классическое определение вероятности связано с понятием элементарного события. Рассматривается некий набор Ω равновероятных событий Ai, которые в совокупности дают достоверное событие. И тогда все хорошо: всякое событие разбивается на элементарные, после чего считается его вероятность.

Однако, далеко не всегда исходный набор Ω (т.е. пространство всех элементарных событий) является конечным. Например, в качестве Ω можно взять ограниченное множество точек на плоскости или отрезок на прямой.

В качестве события A можно рассмотреть любую подобласть области Ω. Например, фигуру внутри исходной фигуры на плоскости или отрезок, лежащий внутри исходного отрезка на прямой.

Заметим, что элементарным событием на таком множестве может быть только точка. В самом деле, если множество содержит более одной точки, его можно разбить на два непустых подмножества. Следовательно, такое множество уже неэлементарно.

Теперь определим вероятность. Тут тоже все легко: вероятность «попадания» в каждую конкретную точку равна нулю. Иначе получим бесконечную сумму одинаковых положительных слагаемых (ведь элементарные события равновероятны), которые в сумме по-любому больше P(Ω) = 1.

Итак, элементарные события для бесконечных областей Ω — это отдельные точки, причем вероятность «попадания» в любую из них равна нулю. Но как искать вероятность неэлементарного события, которое, подобно Ω, содержит бесконечное множество точек? Вот мы и пришли к определению геометрической вероятности.

Определение

Геометрическая вероятность события A, являющегося подмножеством множества Ω точек на прямой или плоскости — это отношение площади фигуры A к площади всего множества Ω:

Задача

Мишень имеет форму окружности радиуса 4. Какова вероятность попадания в ее правую половину, если попадание в любую точку мишени равновероятно? При этом промахи мимо мишени исключены.

Решение

Взглянем на картинку: нас устроит любая точка из правого полукруга. Очевидно, площадь S(A) этого полукруга составляет ровно половину площади всего круга, поэтому имеем:

Ответ

0,5

Чтобы наглядно представить себе, что такое геометрическая вероятность, возьмите лист бумаги и начертите произвольную фигуру. Треугольник, квадрат или окружность — что угодно. Затем возьмите острый, хорошо заточенный карандаш и ткните им в любую точку фигуры. Повторите этот нехитрый процесс несколько раз. Если исключить попадания за пределами фигуры, то получится вот что:

Вероятность попадания в фигуру равна P(Ω) = 1. Это вполне логично, поскольку вся наша фигура — это и есть пространство элементарных событий Ω;

Если некоторую точку (элементарное событие) отметить заранее, то вероятность попадания именно в нее равна нулю. Даже если специально «целиться», точного попадания не будет. Ошибка составит тысячные доли миллиметра, но не ноль;

Теперь возьмем две точки. Вероятность попадания в любую из них все равно ноль. Аналогично, если взять 3 точки. Или пять — без разницы.

Этот опыт показывает, что конечная сумма нулевых слагаемых всегда равна нулю. Но что происходит, когда слагаемых становится бесконечно много? Здесь ситуация не так однозначна, и возможны три варианта:

Сумма равна нулю, как и для конечного набора точек. Если в нашем опыте отмечать точки до бесконечности, вероятность попадания в их объединение все равно нулевая;

Сумма равна некоторому положительному числу — этот случай принципиально отличается от первого. Здесь и возникает геометрическая вероятность;

Сумма равна бесконечности — бывает и такое, но сейчас нас это не интересует.

Почему так происходит? Механизм возникновения положительных чисел и бесконечностей связан с понятием счетности множества. Кроме того, надо понимать, что такое мера Лебега. Впрочем, эти знания действительно нужны вам, только если вы учитесь на математика.

7. Зависимые и независимые события. Условная вероятность. Теорема об умножении вероятностей зависимых событий. Примеры.

События А , В Е называются независимыми, если Р ( А В ) = Р ( А ) · Р ( В ) .

В противном случае события А и В называются зависимыми.

Пусть вероятность события В не зависит от появления события А.

Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т. е. если условная вероятность события В равна его безусловной вероятности:

РA (В) = Р (В). (*)

Подставив (*) в соотношение (***) предыдущего параграфа, получим

Р (A) Р (В) = Р (В) РB (A).

Отсюда РB (A) = Р (A),

т. е. условная вероятность события A в предположении что наступило событие В, равна его безусловной вероятности. Другими словами, событие A не зависит от события В.

Итак, если событие В не зависит от события A, то событие A не зависит от события В; это означает, что свойство независимости взаимно.

Для независимых событий теорема умножения Р (АВ) = Р (А) РA (В) имеет вид Р (АВ) = Р (А) Р (В), (**)

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Равенство (**) принимают в качестве определения независимых событий.

Два события называют независимыми, если вероятность их совмещения равна произведению вероятностей этих событий; в противном случае события называют зависимыми.

На практике о независимости событий заключают по смыслу задачи. Например, вероятности поражения цели каждым из двух орудий не зависят от того, поразило ли цель другое орудие, поэтому события «первое орудие поразило цель» и «второе орудие поразило цель» независимы.

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А.

Условной вероятностьюдва обозначения) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.