14.Частковыя вытворныя вышэйшых парадкаў. Тэарэма аб роўнасці змешаных вытворных.

Кали ф-я z=f(x) мае у нек-м мн-в D з частковую вытворную по адной СА зменных то гэта вытворная сама зъяуляецца фун-й 2-х зменных па гэтаму яна таксама можа мець частковыя вытворныя для разгледжанай ф-и яны будуць зъяуляцца частковай вытворнай 2-га парадку. Кали 1-я частковая вытворная была узята па X, то 2-я яе вытворная будзем абазначаць так:

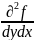
Аналагична вызнач частковая вытворная 3-га,4-га,n-га парадку

Азн1. Частковая вытворная n-га парадку дзе n-натуральн ф-и f назыв частковую вытворную 1-га парадку па якой-небудзь зменнай ад любой частковай вытворнайпарадку (n-1) ф-и f (пад частков вытворн 0-га парадку разумеем саму функ-ю)

Частковая вытворная вышэйшага парадку узятая па розным зменным наз зменнай вытворнай

Азн2. Ф-я f наз n-разоу выферансавальнай у п-це (x0,y0) инт D, кали яна мае у некатор наваколли гэтага п-у усе частк вытворныя (n-1) парадку.

Тэарэма (Аб роунасци змешаных вытворных): Нях. Ф-я f(x,y) у некат-м наваколли п-ту (x0,y0) мае змешаныя частков вытворныя 2-га парадку 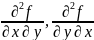прычым яны непарыуныя у п-це (x0,y0) тады у п-це (x0,y0) тады у п-це (x0,y0) гэтыя зменныя вытворныя роуныя памиж сабой г.зн. што

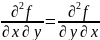
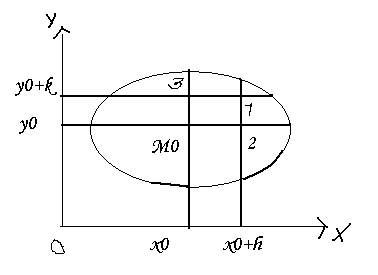
Доказ. Разгл. Выраз

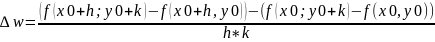
Дзе h,k-дастаткова малыя дадатныя лики што прамавуг [x0,x0+h,y0,y0+k] змяшчаюцца у разгляд наваколли п-ту (х0;у0). Разгл дапаможн ф-ю [x0,x0+h]:

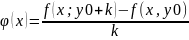
Тады выраз для w запишацца

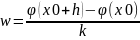
Зн-м вытворную у (1).

Вытворная у правай частцы иснуюць па умове Т. т.як ф-я мае вытворную на адр [x0,x0+h] то яна и непарыуная на гэтым адрэзку па-гэтаму да яе можна прымяниць фор-лу кананичных прыростау Лагранджа.

Т.Ч. мы атрымали:

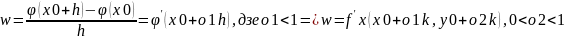
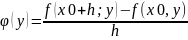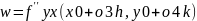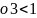Т.ч. кали увесци новую ф-ю то аналагична разваж можна атрымать што , дзе 0< 0<

З атрыманнага роун можна записаць . ))

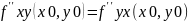Заувага: З сцвярж даказанага у Т. можа быць дак-на для змешаных вытворных любога парадку папрыклад пры умове непарыунасци будзе выконвацца

15.Дыферанцыялы вышэйшых парадкаў

Нях ф-я 2-ы непарыуная дыферанц на мн. D з . Вядома што яе поуны дыферанц записываецца у выглядзе

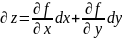
Гэты дыферанцыял зъяуляецца функцыяй ужо 4-х зменных x,y пры фиксаваных dx I dy дыферанс. гэта ф-я 2-х зменных выличан для такой ф-и дэферанц-л прычым у якасци будзем браць dx I dy.Т.ч. падличаны дыф-л ад 1-го дыферанц наз. 2-м дыферанц-м ци дыферанц-ам 2-га парадку ф-и z=f(x,y) и абазначаецца

Выконв ул-ци дыферанц-ла.

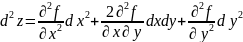(1)

Аналагична можна зн-ци

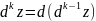
Для складанай ф-и z=f(x,y) x=x(u,v) y=y(u,v)

2-ги дыферанц не будзе выраж па фор-ле (1) г.зн. што для дыфер парадку n болш або роунага 2 не мае месца ул-ци инварыянтнасци формы. Для склад ф-и дыферанц 2-га парадку будзе вызначацца так

(2)

Заувага: Нях х и у залежаць ад u и v линейна, тады формула (2) супадае з (1) т.як.

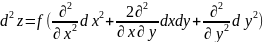
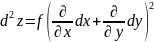
16. Формула Тэйлара для ф.Д.З.

Разгледзім ф-ыю F(t), як вядома ф-ыя F(t) пры умове існавання яе вытворн да (n+1)-ага парадку ўключна можа быць раскладзена ф-ла Тэйлара ў наваколлі некаторага п. t₀

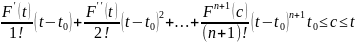F (t)= F(t₀) + (1)

\

1-ы дыфер астаткавы складнік у форм Лагранжа

Прычым у ф-ле канечнага прыроста астаткавы складнік запісаны ў форме Лагранжа можна ўявіць у выглядзе:

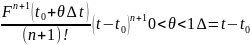
Абазначым , тады F(t)-F(t₀)=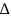 F(t₀), формула (1) запішацца ў выглядзе:

F(t₀)= dF(t₀) + 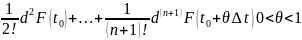(2)

Ф-лу (2) распаўсюдзім на ф-ыю 2-х зменных і атрымаем ф-лу Тэлара для яе выраж праз дыфер. Няхай у наваколлі п.(x₀, y₀) ф-ыя 2-х зменных z=f(x,y) мае непарыўн вытворныя да (n+1)-ага парадку уключна. Нададзім п.x₀ і y₀ прыросты адпаведна x і y , прычым п.(x₀+ x, y₀+ y) не выходзіць за межы разглядаемага наваколля. Увядзем новую зменную наступным чынам x=x₀+t x, y=y₀+t y, , t=t-t₀, t=1, t₀=0, t=1. Падставіўшы гэтыя значэнні x і y у ф-ыю z атрымаем складаную ф-ыю зменнай t

*

Пры гэтым

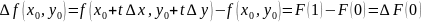
Ф-ыя F(t) з’яўл кампазіц ф-ый f(x, y), x=x₀+t x, y=y₀+t y па гэтаму яна будзе дыф (n+1) колькасць разоў на адрэзку [0,1]

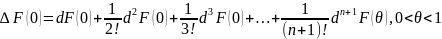(3)

Пяройдзем у ф-ле (3) ад ф-ыі F да ф-ыі f(x, y)

*:

… … … … … … … … … …

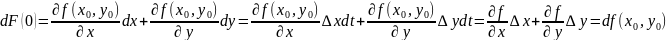
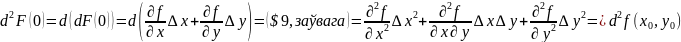
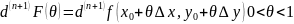
Падставім у (3):

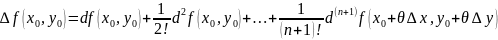
(4)-ф-ла Тэйлара для ф-ыі 2-х зменных. Т.ч. даказана наступная тэарэма

Тэарэма. Няхай ф-ыя z=f(x, y) непарыўна разам со сваімі частковымі вытворнымі да (n+1) парадку уключна ў некаторых наваколлях п.( x₀, y₀), тады ў гэтым наваколлі справядліва ф-ла Тэйлара (4)