
- •1.Паняцце функцыі многіх зменных. Узроўні функцыі многіх зменных
- •2.Ліміт функцыі дзвух зменных (ф.Д.З), непарыўнасць, раўнамерная непарыўнасць
- •3.Частковыя вытворныя ф.Д.З. Дыферэнцавальнасць ф.Д.З. Геаметрычны сэнс частковых вытворных.
- •4. Частковыя вытворныя ф.Д.З. Сувязь паміж дыферынцаванасцю і існаваннем частковых вытворных.
- •5. Поўны дыферэнцыял ф.Д.З. І яго ўласцівасці.
- •6. Поўны дыферэнцыял ф.Д.З. І яго геаметрычны сэнс.
- •7.Дыферанцавальнасць складанай функцыі. Даказаць тэарэму1.
- •8. Дыферанцавальнасць складанай функцыі. Даказаць тэарэму2
- •9.Дыферэнцавальнасць складанай функцыі.
- •10. Інварыянтнасць формы першага дыферанцыяла.
- •11. Вытворная ў накірунку, яе існаванне і вылічэнне.
- •13.Неяуныя функцыі.Тэарэма аб існаванні няяўнай функцыі.
- •14.Частковыя вытворныя вышэйшых парадкаў. Тэарэма аб роўнасці змешаных вытворных.
- •15.Дыферанцыялы вышэйшых парадкаў
- •16. Формула Тэйлара для ф.Д.З.
- •17. Пункты лакальнага экстрэмума ф.Д.З. Неабходная і дастатковыя ўмовы існавання лакальных экстрэмумаў.
- •18. Пункты ўмоўнага экстрэмума ф.Д.З. Правіла Лагранжа знахожжання пунктаў умоўнага экстрэмума.
- •19. Паняцце двайного інтэграла, умовы яго існавання (доказы).
- •20. Паняцце двайного інтэграла, ято ўласцівасці (доказы).
- •21. Паняцце двайного інтэграла, геаметрычны сэнс.
- •22.Паняцце двайнога інтэграла, вылічэнне двайнога інтэграла паўторным інтэграваннем.
- •23.Крывалінейныя каардыеаты на каардынатнай пл—сці. Прыклады.
- •24. Якабіан. Формула замены зменнай ў двайным інтэграле.
- •25 Паняцце трайнога інтэграла, умовы яго існавання і ўл-сці (доказы).
- •26 Вылічэнне трайнога інтэграла
- •27.Замена зменнай у трайным интэграле. Цылиндрычныя и сферычныя каардынаты.
- •28. Паняцце плошчы паверхні
- •29. Формула плошчы гладкай паверхні
- •30. Крывалінейны інтэграл па даўжыне дугі і яго ўласцівасці
- •31. Крывалінейны інтэграл па каардынатах і яго ўласцівасці.
- •32.Вылічэнне крывалінейнага інтэграла другога тыпу.
- •33. Формула Грына.
- •34. Крывалінейныя інтэгралы, якія не зал.Адшляху інтэгравання. Т-ма 1,3.
- •35. Крывалінейныя інтэгралы, якія не зал.Ад шляху інтэгравання. Т-ма 2.
- •36. Аднаўленне ф-цыі па яе поўнаму дыферэнцыялу.
- •Паняцце функцыі многіх зменных. Узроўні функцыі многіх зменных.
9.Дыферэнцавальнасць складанай функцыі.
Тэарэма
3.Разгледзім
n-мерный
выпадак. Няхай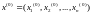 у
наваколлі пункта зададзена функцыя
у
наваколлі пункта зададзена функцыя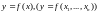 і
на некаторым мностве
і
на некаторым мностве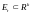 зададзена
функцыя
зададзена
функцыя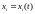 ,
дзе
,
дзе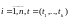 .Няхай
.Няхай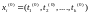 .
Калі функцыя
.
Калі функцыя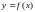 дыферанцавальная
у пункце
дыферанцавальная і у пункце
дыферанцавальная
у пункце
дыферанцавальная і у пункце
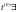 частковыя
вытворныя
частковыя
вытворныя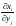 ,
,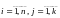 ,
тады складаная функцыя
,
тады складаная функцыя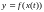 мае
у пункце
мае
у пункце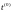 частковыя
вытворныя
частковыя
вытворныя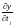 ,
якая роўна
,
якая роўна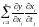

Азначэнне дыферанцавальнасці 1: Калі поуны прырост ф-ыі f у п( , ) можна прадставіць у выглядзе дзе -бясконца малыя велічыні залежныя ад , калі ,
то ф-ыя f наз дыферанцавальнай у п ( , )
Азначэнне дыферанцавальнасці 2: Ф-ыя f наз дыферанцавальнай у п ( , ), калі існуюць два такія лікі А,В, што дзе дзе
Азначэнне поунага прыроста: Поуным прыростам ф-ыі f у п ( , ) наз той прырост ф-ыі, які яна атрымоувае пры адвльных прырастах абіх аргументау. Гэта значыць
Азначэнне частковай вытворнай: Калі існуе канечны ( ), то ен наз частковай вытворнай ф-ыі f па зменнай x(па зменнай y)і абазначаецца , , , .
10. Інварыянтнасць формы першага дыферанцыяла.
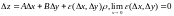
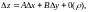
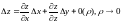
Азначэнне:
У выпадку дыферанцавальнасці функцыі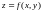 у
пункце
у
пункце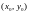 лінейная
функцыя
лінейная
функцыя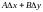 адносна
зменных
адносна
зменных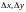 называецца
поўным
дыферанцыялам
ці проста дыферанцыялам функцыі ў
пункце
і
абазначаецца
называецца
поўным
дыферанцыялам
ці проста дыферанцыялам функцыі ў
пункце
і
абазначаецца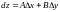 .
Дамовілісь
.
Дамовілісь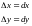
Дыферанцыял
запісваецца ў выглядзе: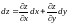
Тэарэма1:
Няхай
функцыя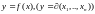 вызначана
ў некаторым наваколлі пункту
вызначана
ў некаторым наваколлі пункту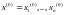 ,
а функцыя
,
дзе
,
а функцыя
,
дзе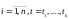 вызначана
ў некаторым наваколлі пункта
вызначана
ў некаторым наваколлі пункта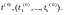 Няхай
Няхай
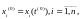 тады
калі функцыя
дыферанцавальная
ў пункце
тады
калі функцыя
дыферанцавальная
ў пункце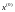 ,
а
,
а
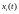 дыферанцавальная
ў пункце
,
дыферанцавальная
ў пункце
,
то складаная функцыя вызначана ў некаторым наваколлі пункту і дыферанцыяльна ў гэтым пункце, пры гэтым дыферанцыял мае выгляд:
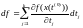 ці
ці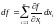
Доказ:Гэтая тэарэма і з’яўляецца выразам уласцівасцей інварыянтнасці поўнага дыферанцыяла адносна выбару зменных. Уласцівасці інварыянтнасці формы першага дыферанцыяла дапамагае высвятліць наступныя правіла дыферанцавання:
Калі
функцыі
 і
і
 функцыі
некаторага ліку зменных, то можна з
дапамогай гэтай тэарэмы атрымаць
наступныя правіла:
функцыі
некаторага ліку зменных, то можна з
дапамогай гэтай тэарэмы атрымаць
наступныя правіла:
1.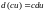
2.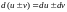
3.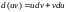
Доказ
3:Разгледзім
функцыі 2-х зменных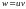
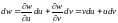 .
Паводле інварыянтнасці формы першага
дыферанцыяла выраз
.
Паводле інварыянтнасці формы першага
дыферанцыяла выраз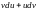 з’ўляецца дыферанцыялам і ў выпадку,
калі
і
з’яўляюцца функцыямі ад якіх-небудзь
зменных.
з’ўляецца дыферанцыялам і ў выпадку,
калі
і
з’яўляюцца функцыямі ад якіх-небудзь
зменных.
4.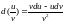
5.
Поўным дыферанцыялам функцыі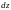 адрозніваецца ад поўнага прыроста
адрозніваецца ад поўнага прыроста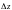 больш высокага парадку маласці
больш высокага парадку маласці
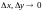 ,
чым велічыня
,
чым велічыня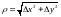
Доказ
5:Калі
функцыя дыферанцыяльна, то яе поўны
прырост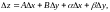 дзе
дзе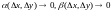 ,
калі
,
калі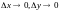
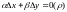 для
гэтага нам патрэбна даказаць, што
для
гэтага нам патрэбна даказаць, што
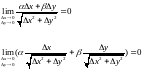
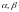 -бясконца
малыя,
-бясконца
малыя,
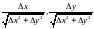 -абмежаваныя.
-абмежаваныя.
Гэтая ўласцівасць можа быць сфармулявана так:Поўны дыферанцыял функцыі ёсць галоўная лінейная частка поўнага прыроста.
6.
Пры дастаткова малых
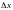 і
і
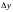 ,
а значыць і
і
можна
прыблізна вылічыць поўны дыферанцыял
роўны поўнаму прыросту функцыі, г.зн.
,
а значыць і
і
можна
прыблізна вылічыць поўны дыферанцыял
роўны поўнаму прыросту функцыі, г.зн.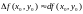
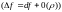 .
.
Гэта формула выкарыстоўваецца для вылічэння набліжанага значэння функцыі і для ацэнкі хібнасцей вылічэнняў(гл.для функцыі адной зменнай).
Заўвага:Здабытак
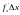 і
і
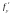 называецца частковымі дыферанцыяламі
функцыі
называецца частковымі дыферанцыяламі
функцыі
