5. Поўны дыферэнцыял ф.Д.З. І яго ўласцівасці.

Азнач: У выпадку дыферынц. функц. z = f(x , y) у п. (х₀ , у₀) лінейная функцыя Ax+By адносна зменнай x і y назыв. поўным дыферынцыялам (ці проста дыферынцыялам ) функц. f у п.(x₀ , y₀) і абазначаецца праз dz.

dz = Adx + Bdy, дамовімся што x = dx, y = dy  dz =

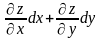
Уласцівасці(f і g функцыі двух зменных)

1⁰. d( c f (x,y) ) = c d ( f ( x , y ) )

2⁰. d( f ( x , y )  g ( x , y ) ) = df  dg

3⁰. d( f g ) = f d g + g d f

Д-з: Няхай w = f g,

4⁰.

5⁰. Поўны дыферынцыял функцыі dz адрознів. ад поўнага прыросту функц. z на велічыню больш высокага парадку маласці , калі x0, y0, чым велічыня

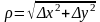
Д-з: z(x₀ , y₀) = Ax + By + x + y (1)

Калі функц. дыфер., то поўны прырост функц. можна прэдставіць у выглядзе (1), дзе (x , y)0, трэба даказаць: x + y = o(ρ)

Для гэтага нам трэба дак-ць, што 0

0 (, —б.м.п., x/.., y/..-абмеж.) ■

6⁰. Пры дастаткова малых x і y, а значыць dz і z можна прыблізна лічыць поўны дыфер. = поўнаму прыросту функц., г.зн. ( )

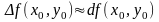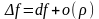Гэта формула выкарыст. для выліч. набліжаннага знач. функцыі і для ацэнкі хібнасці вылічэн.

6. Поўны дыферэнцыял ф.Д.З. І яго геаметрычны сэнс.

Азнач: У выпадку дыферынц. функц. z = f (x , y) у п. (х₀ , у₀) лінейная функцыя Ax + By адносна зменнай x і y назыв. поўным дыферынцыялам (ці проста дыферынцыялам ) функц. f у п.(x₀ , y₀) і абазначаецца праз dz.

dz = Adx + Bdy, дамовімся што x = dx, y = dy  dz =

Геаметрычн. сэнс:

Н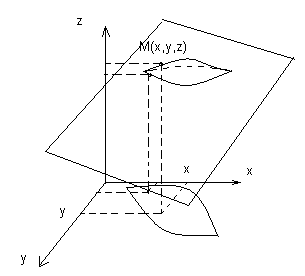 яхай z = f(x , y), вызначана у некатор. наваколлі п-ту (x₀ , y₀), графікам такой функц. з’яўл. некатор. паверхня прасторы R³.

Няхай п-т M₀ (x₀ , y₀ , z₀) належыць графіку ф-ыі z = f (x , y), праз гэты п-т праходз. шмат пласкасцей, якія не з’яўл. паралельн. пл-ці XOY, іх раўнанні маюць выгляд:

Z - z₀ = A ( X - x₀ ) + B ( Y - y₀ )

Z = z₀ + A( X - x₀ ) + B ( Y - y₀ )

Азнач2.: Плоскасць якая прах праз п-т M₀ графіка функц. f і задавальняе наступн. умове: рознасць паміж знач. функц. і аплікатай пл-ці у п-це (x , y)  U_ (x₀ , y₀) і мае прэдстаўленне x + y, дзе 0 0 калі x0, y0, назыв. плоскасцю датычнай да графіка функц. f у п.M₀. Можна сказать, што рознасць паміж аплікатамі графіка функц. і датычнай пл-ці з’яўл. бяс. малой веліч. больш высокага парадку маласці чым ρ, калі x0, y0.

З азн2 і раўнаняў пл-ці атрымаем:

f(x , y) – z = x + y  f(x,y) - z₀ - A(X - x₀) - B(Y - y₀) = x + y

f(x , y) - f(x₀ , y₀) = A(X - x₀) + B(Y - y₀) + x + y

f(x₀ , y₀) = A(X - x₀) + B(Y - y₀) + x + y

Атрымалі ўмову дыфер. функц. у п-це, г.зн. што неабх і даст умова  датычн. пл-ці да паверхні ў п M₀ з’яўл. дыфер.функц. у п-це.

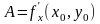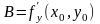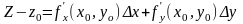Т.як , , то раунанне датычнай пл-ці можа быць запісана ў выглядзе: - раунанне датычнай плоскасці

Z - z₀ = dz  геаметр. сэнс дыферынцыяла: дыферынц.функц. выражае прырост аплікаты датычнай пл-ці да графіка функц. f у пункце(x₀ , y₀ ,z₀) пры пераходзе ад п.(x , y) да п. (x₀ , y₀).

Азнач3: Прамая, якая з’яўл. -ай да датычнай пл-ці пераведзеннай у п. (x₀ , y₀ ,z₀) да графіка функц. z=f(x , y) назыв. нармаллю да графіка функц. f у п. (x₀ , y₀ ,z₀) і яе раўнанне мае выгляд: