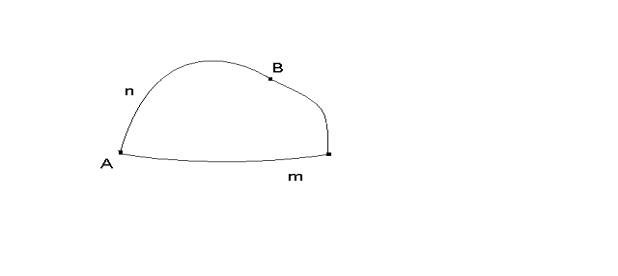
30. Крывалінейны інтэграл па даўжыне дугі і яго ўласцівасці

Разгледзім на XOY нек выпрастальную крывую, якая не мае пунктаў самаперасячэння і часткаў саманалажэння. Нях гетая крывая зададзена параметрычна: Пачатак А, канец В.

Дапусцім далей , што ф-цыя вызначана і непарыўная ўздоўж крывой Г.зн., што пункт M(x;y) крывой адпавядае пэўнаму значэнню ф-цыі f(x;y) і калі , .

Разаб’ём [α;β] пунктамі α=t₀<t₁<t₂<…< <t_k<…<t_n=β на n частковых адрэзкаў [t_k-1;t_k]. Т.я. на крывой адпавядае (.) M_k(x_k,y_k), то пры разбіўцы [α;β] на частковыя ўся крывая АВ разаб’ецца на n частковых дуг: М₀М₁, М₁М₂, … ,M_k-1M_k…

Выберам на частковай дузе M_k-1M_k (.) N_k(ξ_k ,η_k),які адпавядае нек значэнню τ _k, параметра t. Т.ч. ξ_k=φ (τ _k), =ψ(t_k), , t_k-1 τ _k t_k

Саставім інтэгральную суму (2), дзе – даўжыня часковай дугі M_k-1M_k

Азн. Лік I наз лімітам інтэгральнай сумы σ, калі найб з даўжынь = λ, Δ x_k=λ, Δ y_k =λ–>0, калі

Азн. Калі , то ліміт наз крывалінейным інтэгралам 1-га роду (крывалінейным інтэгралам па даўжыне дугі) ад ф-цыі f(x;y) па крывой і абазн: ці , т.ч. .

Заўв.1 З выгляду інтэгральнай сумы σ відавочна, што крывалін інтэграл 1-га роду не залеж ад накірунку інтэгравання, а вядзе за сабой змяненне знака інтэграла:

Заўв.2 Калі крывая =AB з восі OX, то f(x;y)= f(x;0)= F(x), = Δ x_k . Па гэтаму крывалінейны інтэграл 1-га роду з’яўл вызначаным інтэгралам, у гэтым выпадку:

Уласцівасці:

1. Калі ф-цыя f(x;y) і інтэгравальныя па крывой , то па крывой будзе інтэграв і іх сума і рознасць, пры гэтым

2. Калі f інтэгравальная па і k=const, то

3. Калі дуга складаецца з 2-х дуг , і калі для ф-цыі f крывалінейны інтэграл па , то для ф-цыі f будуць інтэгралы па крывым :

4. Калі інтэгравальная па , то ф-цыя | f | так сама інтэграв па крывой :

5. (Ф-ла сярэдняга значэння) Калі ф-цыя f непар ўздоўж крывой , то (.) М* | = f(M*)∙ , дзе – даўжыня крывой

31. Крывалінейны інтэграл па каардынатах і яго ўласцівасці.

1-га роду: 1.Калі функцыі і інтэгравальныя па крывой L, то па крывой L будзе з’яўляцца інтэгравальнай іх сума і рознасць. Пры гэтым:

2. Калі f-інтэгравальная па L і k-const, то інтэграл =k

3. Калі дуга L = (складз.з 2-х дуг) і калі для ф. будуць па крывым і ,прычым інтэграл уздоўж L:

= +

4. Калі f-інтэгравальная па L, то |f| таксама інтэгр. па крывой L, прычым: | |

5. Формула сярэдняга значэння: Калі ф.f –непарыўна ўздоўж крывой L,то п-т = f( ) , дзе -даўжыня крывой L.

2-га роду: 1. Калі крывую L, па якой вядзецца інтэграванне разбіць на часткі L = , то крывалінейны інтэграл па L= суме інтэгралаў па яе часткам узятым у тым жа накірунку = +…+

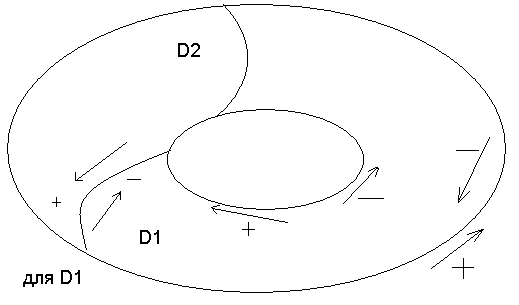
2. Калі крывая L-замкнутая, то велічыня крывалінейнага інтэграла па L не залежыць ад таго,які пункт па L узяць за пачатковы

3. Калі мноства D-абмежаванае крывой L разбіць на мноствы і , то крывалінейны інтэграл па L у некаторым накірунку будзе роўны суме крывалінейных інтэгралаў па і ,якія абмяжоўваюць мноствы і ўзятых у тым жа самым накірунку

=>

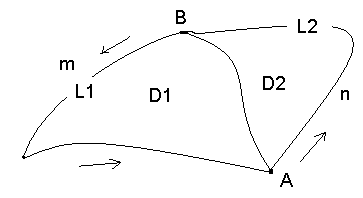
Заўвага. Калі L-замкнутая крывая(контур), то з 2-х магчымых накірункаў яе абхода мы будзем называць дадатным накірунак, пры якім вобласць абмежаваная контурам застаецца па левы бок у адносіне да пункту, які ажыццяўляе яго(абход).