27.Замена зменнай у трайным интэграле. Цылиндрычныя и сферычныя каардынаты.

Аналагична пераутварэнню пласкасцей можна разглядаць пераутварэнне прасторавых вобласцей. Няхай дадзены дзве замкнутыя прасторавыя вобласци D и D’, у прамавугольнай систэме каардынат одпаведна Oxyz и O’ξηϒ и няхай гэтыя вобласци звязаны памиж сабой узаемна адназначнай адпаведнасцю якая выражаецца формулами (2).

Ф-цыи (2) з’яуляюцца непарыуными , разам са сваими вытворными, а лики ξ,η,ϒ называюцца крывалинейными каардынатами пункту (x,y,z) прасторы Oxyz.

Р

X=r*cosφ

Y=r*sinφ

r>=0

φ∊[0,2π]

z∊[-∞,+∞]

азгледзем цылиндрычныя каардынаты у гэтай систэме. Становишча пункту M, у прсторы вызначаецца палярными каардынатами r и φ. Праекцыи пункту M на плоскасть Oxy и апликатай z самаго пункту M.

y

x

z

M

M’

Пытанне аб пераутварэнни трайнога интэграла пры такой замене, выражаецца пры дапамозе формулы

M’

x

z

y

M

φ

ψ

r

O

z

ψ

ψ

r

M’

M

OM’=rsinψ r>=0 φ∊[0,2π] ψ∊[0,π]

Становишча пункту M у прасторы вызначаецца адлегласцю r, ад гэтага пункту да пачатку каардынат , вугал φ памиж воссю Ox и праекцыяй адрэзку OM на плоскасць xOy и вуглом ψ памиж OM и Oz.

Таким чынам формулы якия звязваюць сферычныя каардынаты з прамавугольными будуць мець выгляд

x=rsinψcosφ y=rsinψsinφ z=rcosψ

трайны интэграл па E

28. Паняцце плошчы паверхні

Няхай паверхня G зададзена яўна z=f(x;y) (1) Няхай x і y зменныя ў квадравальнай вобласці D плоскасці XOY. Фунццыя f непарыўная на D і мае непарыўныя частковыя вытворныя. Пры такіх умовах паверхня (1) у пункце М₀ (x₀;y₀;z₀) мае датычную плоскасць. Разаб’ём вобласць D сеткай крывых на n адвольных частак D₁, D₂ ,…,D_n – Т-разбіўка вобласці D. Няхай S(D_k) – плошча кожнай D_k

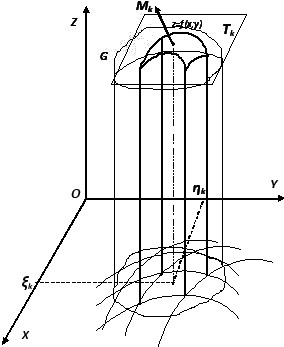
Цыліндрычныя столбікі, пабудаваныя на адвольнай з D_k як на аснове, разаб’юць паверхню G на n частак G₁, G₂, …, G _n.

На D_k возьмем пункт N_k(ξ_k,η_k), k= . Гэтаму пункту на куску паверхні G _k будзе адпавядаць пункт M_k(ξ_k,η_k,γ_k), дзе γ_k = f(ξ_k,η_k). У кожным M_k пабудуем датычную пл-ць да паверхні T_k і нармаль . з цыліндраў столбікаў выража на такой датычнай пл-ці фігуру, якую абазн T_k, а яя плошчу – S(T_k).

Калі разбіўка вобласці D становіцца мяльчэй, то плоскія фігуры T_k будуць бліжэй прымыкаць да адпаведнай часткі паверхні, па гэтаму можна прыблізна лічыць значэнне S(T_k) плошчай часткі паверхні G _k . Тады сума (2) з’яўляецца прыблізна значэннем плошчы паверхні.

Азн. Ліміт сумы (2), які не залежыць ад разбіўкі T_D і выбару пунктаў N_k пры ўмове што λ 0, дзе λ – найменшы дыяметр D_k , наз плошчай паверхні.

Азн. Паверхня, якая мае плочшу, наз квадравальнай.

29. Формула плошчы гладкай паверхні

Тэарэма: Плошчу паверхні z=f(x;y) (1) можна вылічыць па формуле:

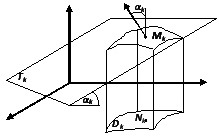
Абазначым праз λ_k вугал паміж датычнай пл-цю ў пункце M_k(ξ_k,η_k, f(ξ_k,η_k)) і пл-цю XOY.

На падстве вядомай формулы аналітычнай геаметрыі S(D_k)=S(T_k)cosα_k , т.е. праекцыя плошчы на пл-ць = праектавальнай плошчы на cos вугла паміж імі. .

З другога боку α_k – паміж OZ і . Па гэтаму cosα_k з’яул кіроўным косінусам вектара нармалі да датычнай пл-ці ў пункце M_k. Вядома (з аналіт геам), што . Тады сума з’яўляецца інтэгральнай: . Т.як функцыя непарыўная на D, то .