
- •1.Паняцце функцыі многіх зменных. Узроўні функцыі многіх зменных
- •2.Ліміт функцыі дзвух зменных (ф.Д.З), непарыўнасць, раўнамерная непарыўнасць
- •3.Частковыя вытворныя ф.Д.З. Дыферэнцавальнасць ф.Д.З. Геаметрычны сэнс частковых вытворных.
- •4. Частковыя вытворныя ф.Д.З. Сувязь паміж дыферынцаванасцю і існаваннем частковых вытворных.
- •5. Поўны дыферэнцыял ф.Д.З. І яго ўласцівасці.
- •6. Поўны дыферэнцыял ф.Д.З. І яго геаметрычны сэнс.
- •7.Дыферанцавальнасць складанай функцыі. Даказаць тэарэму1.
- •8. Дыферанцавальнасць складанай функцыі. Даказаць тэарэму2
- •9.Дыферэнцавальнасць складанай функцыі.
- •10. Інварыянтнасць формы першага дыферанцыяла.
- •11. Вытворная ў накірунку, яе існаванне і вылічэнне.
- •13.Неяуныя функцыі.Тэарэма аб існаванні няяўнай функцыі.
- •14.Частковыя вытворныя вышэйшых парадкаў. Тэарэма аб роўнасці змешаных вытворных.
- •15.Дыферанцыялы вышэйшых парадкаў
- •16. Формула Тэйлара для ф.Д.З.
- •17. Пункты лакальнага экстрэмума ф.Д.З. Неабходная і дастатковыя ўмовы існавання лакальных экстрэмумаў.
- •18. Пункты ўмоўнага экстрэмума ф.Д.З. Правіла Лагранжа знахожжання пунктаў умоўнага экстрэмума.
- •19. Паняцце двайного інтэграла, умовы яго існавання (доказы).
- •20. Паняцце двайного інтэграла, ято ўласцівасці (доказы).
- •21. Паняцце двайного інтэграла, геаметрычны сэнс.
- •22.Паняцце двайнога інтэграла, вылічэнне двайнога інтэграла паўторным інтэграваннем.
- •23.Крывалінейныя каардыеаты на каардынатнай пл—сці. Прыклады.
- •24. Якабіан. Формула замены зменнай ў двайным інтэграле.
- •25 Паняцце трайнога інтэграла, умовы яго існавання і ўл-сці (доказы).
- •26 Вылічэнне трайнога інтэграла
- •27.Замена зменнай у трайным интэграле. Цылиндрычныя и сферычныя каардынаты.
- •28. Паняцце плошчы паверхні
- •29. Формула плошчы гладкай паверхні
- •30. Крывалінейны інтэграл па даўжыне дугі і яго ўласцівасці
- •31. Крывалінейны інтэграл па каардынатах і яго ўласцівасці.
- •32.Вылічэнне крывалінейнага інтэграла другога тыпу.
- •33. Формула Грына.
- •34. Крывалінейныя інтэгралы, якія не зал.Адшляху інтэгравання. Т-ма 1,3.
- •35. Крывалінейныя інтэгралы, якія не зал.Ад шляху інтэгравання. Т-ма 2.
- •36. Аднаўленне ф-цыі па яе поўнаму дыферэнцыялу.
- •Паняцце функцыі многіх зменных. Узроўні функцыі многіх зменных.
23.Крывалінейныя каардыеаты на каардынатнай пл—сці. Прыклады.
Няхай
зменныя х і у
з’яул. функцыямі дзвюх другіх незалежных
зменных. Г. зн. х=х(u,v), у=у(u,v) (1). Прычым
х(u,v) і у(u,v) - непар. і маюць непар.
частковыя вытворныя па u,v на некаторым
мн-ве Д. Пры пастаянным значэнні адной
з пераменных u ці v, пункт
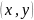 апісвае некаторую крывую. Розным знач.
u адпавядае сістэма ліній, якія наз. u
лініямі. Аналагічна і для v. Т. ч. любой
пары (u,v) адпавядае некаторы пэуны пункт
,
як пункт перасяч. u і v ліній. Будзем
разглядаць мн-ва Д плоскасці ХОУ, унутры
якога, кожная u-лінія перасякаецца з
кожнай v-лініяй небольш чым у адным
пункце. Прычым праз кожны пункт мн-ва Д
абавязкова праходзяць і u, і v лініі. Для
такога мн-ва адпаведнасць пар знач.
з аднаго боку і пар (u,v) – з другога, будзе
узаемна-адназначнай. Т.ч. пункт
плоскасці ХОУ адназначна вызначаецца
каард. u,v, якія наз. для яго крывалін.
каард. Калі u,v разгляд. як прамавугольныя
каардынаты у сістэме каардынат UOV, то
на ей мн-ву Д будзе адпавядаць Д”. Прычым
адпаведнасць паміж Д і Д” будзе
узаемна-адпаведным. Калі пункт (u,v)
апісвае граніцу мн-ва Д”, то адпаведны
пункт
будзе апісваць граніцу мн-ва Д. Т. ч. (1)
адназначна выражаецца адносна u і v. Г.
зн. u=u(x,y),
v=v(x,y)
(2). Т. ч. мы разглядзелі пераутварэнне
плоскасці UO”V
на плоскасць ХОУ , якая задаецца формуламі
(1) і наадварот.
апісвае некаторую крывую. Розным знач.
u адпавядае сістэма ліній, якія наз. u
лініямі. Аналагічна і для v. Т. ч. любой
пары (u,v) адпавядае некаторы пэуны пункт
,
як пункт перасяч. u і v ліній. Будзем
разглядаць мн-ва Д плоскасці ХОУ, унутры
якога, кожная u-лінія перасякаецца з
кожнай v-лініяй небольш чым у адным
пункце. Прычым праз кожны пункт мн-ва Д
абавязкова праходзяць і u, і v лініі. Для
такога мн-ва адпаведнасць пар знач.
з аднаго боку і пар (u,v) – з другога, будзе
узаемна-адназначнай. Т.ч. пункт
плоскасці ХОУ адназначна вызначаецца
каард. u,v, якія наз. для яго крывалін.
каард. Калі u,v разгляд. як прамавугольныя
каардынаты у сістэме каардынат UOV, то
на ей мн-ву Д будзе адпавядаць Д”. Прычым
адпаведнасць паміж Д і Д” будзе
узаемна-адпаведным. Калі пункт (u,v)
апісвае граніцу мн-ва Д”, то адпаведны
пункт
будзе апісваць граніцу мн-ва Д. Т. ч. (1)
адназначна выражаецца адносна u і v. Г.
зн. u=u(x,y),
v=v(x,y)
(2). Т. ч. мы разглядзелі пераутварэнне
плоскасці UO”V
на плоскасць ХОУ , якая задаецца формуламі
(1) і наадварот.
Прыклады:
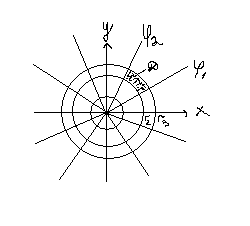
Палярныя
каардынаты x=r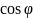 y=r
y=r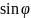 ,
r
0,
0
,
r
0,
0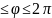 .
.
Калі
r
і
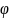 адкладваюць у прамавуг. сістэме каардэн.
r
адкладваюць у прамавуг. сістэме каардэн.
r
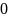 ,
дзе r-
абсцысса,
-
ардыната, то любы пункт (
,
дзе r-
абсцысса,
-
ардыната, то любы пункт (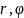 )
будзе адпавядаць адзіны пункт
,
пры гэтым на плоскасці ХОУ кожнаму
пастаяннаму
)
будзе адпавядаць адзіны пункт
,
пры гэтым на плоскасці ХОУ кожнаму
пастаяннаму
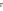 будзе адпавядаць акружнасць з цэнтрам
у пачатку каардынат і радыусам
.
А любое значэнне
(пастаяннае)
у плоскасці ХОУ – промні з пачаткам у
пункце (0,0).
будзе адпавядаць акружнасць з цэнтрам
у пачатку каардынат і радыусам
.
А любое значэнне
(пастаяннае)
у плоскасці ХОУ – промні з пачаткам у
пункце (0,0).
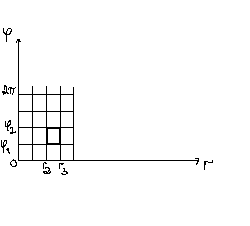
24. Якабіан. Формула замены зменнай ў двайным інтэграле.
Выдзелім
на плоскасці UO”V
бясконца малы прамавугольнік:
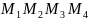 ,
са старанамі du, dv. Яго стораны паралельны
восям О” U, O”V.
Адлюстраваннем гэтага прамавугольніка
на плоскасць ХОУ будзе крывалінейны
чатырохвугольнік
,
са старанамі du, dv. Яго стораны паралельны
восям О” U, O”V.
Адлюстраваннем гэтага прамавугольніка
на плоскасць ХОУ будзе крывалінейны
чатырохвугольнік
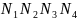 .
.
х=х(u,v), у=у(u,v).
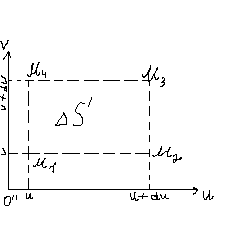
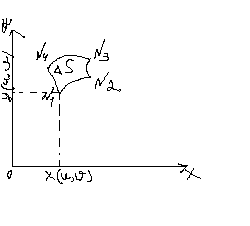
Вяршыні крывалінейнага чатырохвугольніка маюць каардынаты:
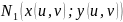
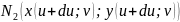
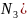
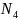 (x(u,v+dv);y(u,v+dv))
(x(u,v+dv);y(u,v+dv))
Вылічым
плошчу
чатырохвугольніка
.
Т
.як дугі
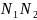 і г. д. вельмі малыя, то прыблізна мы
можам іх лічыць прамымі. Акрамя гэтага
прыросты функцый х(u,v) і у(u,v) мы можам
прыблізна лічыць роунымі дыферынцыялам.
Г. зн.
і г. д. вельмі малыя, то прыблізна мы
можам іх лічыць прамымі. Акрамя гэтага
прыросты функцый х(u,v) і у(u,v) мы можам
прыблізна лічыць роунымі дыферынцыялам.
Г. зн.
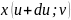 -
-
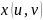 =
=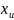 ’du
і значыць
=
’du+
.
’du
і значыць
=
’du+
.
Аналагічна
можна атрымаць, што x(u,v+dv)=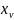 ’dv+
і
’dv+
і
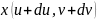 =
’du+
’dv+
.
=
’du+
’dv+
.
Аналагічна і для функцыі у(u,v).
Тады каард. вяршынь крывал. Чатырохвугольніка запішуцца у выглядзе:
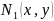
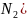 ’du;y+
’du;y+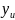 ’du)
’du)
’du+
’dv;y+
’du+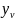 ’dv)
’dv)
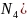 ’dv;
y+
’dv).
’dv;
y+
’dv).
Гэтыя
каард. паказваюць, што праекцыі
,
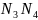 на абоі восі роуныя. Таму можам лічыць,
што
- паралелаграм.
на абоі восі роуныя. Таму можам лічыць,
што
- паралелаграм.
З
аналітычнай геаметрыі вядома, што калі
вяршыні паралелаграма маюць каардынаты
А(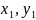 ),
В(
),
В(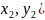 ,
С(
,
С(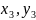 ),то
яго плошчу можна вылічыць як абсалютную
велічыню дэтэрмінанта:
),то
яго плошчу можна вылічыць як абсалютную
велічыню дэтэрмінанта:
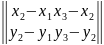
Значыць
S(паралелаграма)=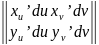 =
=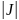 dudv
, дзе Ј=
dudv
, дзе Ј=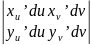 .
.
Ј
наз. дэтэрмінантам Якабі, ці Якабіанам.
S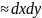 =
dudv=
=
dudv=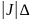 S’.
S’.
Выраз dudv наз. элементам плошчы у крывалінейных каардынатах.
Калі мн-ва Д” плоскасці UO”V прамымі паралельнымі восям, разбіць на бясконца малыя прамавугольнікі, і не улічваць тыя з іх, якія атрымоуваюцца на граніцы мн-ва (яны вельмі малыя), мы тым самым разбіваем мн-ва Д плоскасці ХОУ на крывалінейныя чатырохвугольнікі разгледжанага вышэй выгляду. Калі скласці атрыманыя выразы для плошчау гэтых прамавугольнікау і перайсці да ліміта, калі du і dv імкнуцца да 0, то
S(Д)=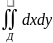 =
=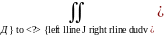 (1).
(1).
Тэар.1
(аб сярэднім для двайнога інтэграла).
Калі функцыя
- непарыуная на замкнутым, звязным мн-ве
Д, то
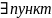 (
(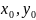 )
)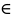 Д
такі, што
Д
такі, што
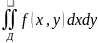 =
=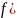 )
) S(Д),
S(Д)
– плошча Д.
S(Д),
S(Д)
– плошча Д.
Тэар.2 (Замена зменнай у двайным інтэграле) Няхай непарыуныя дыферанцаваныя функцыі х=х(u,v), у=у(u,v) ажыцяуляюць адназначнае адлюстраванне абмежаванай замкнутай вобласці Д” плоскасці UO”V па вобласці Д плоскасці ХОУ, тады мае месца наступная роунасць:
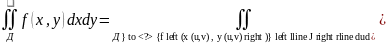 .(2)
.(2)
Доказ:
Разаб’ем
мн-ва Д” прамымі паралельнымі UO”, O”V
адвольным чынам на часткі
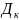 ”.
Тады вобласць Д разаб’ецца на частковыя
мн-вы
і па формуле (1) атрымаем:
”.
Тады вобласць Д разаб’ецца на частковыя
мн-вы
і па формуле (1) атрымаем:
S(
)=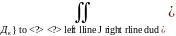 .
Па тэарэме аб сярэднем маем:
.
Па тэарэме аб сярэднем маем:
S(
)=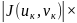 S(
S(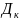 ),
),
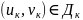 ,
,
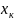 =х
=х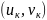 ,
=у
.
,
=у
.
Тады інтэгральная сума функцыі на мн-ве Д можа быць запісана:
х
,
у
)
S(
)=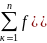 х
,
у
)
х
,
у
)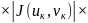 S(
).(3)
S(
).(3)
У левай часцы (3) запісана інтэгральная сума для інтэграла левай часткі (2), а правая частка (3) з’яул. інтэгральнай сумай для інтэграла, які стаіць у правай часцы (2).
Таму,
калі у(3) перайсці да ліміта, калі λ 0
і λ
0
і λ 0,
дзе λ і λ
0,
дзе λ і λ - найбольшыя хорды частковых мн-вау
і
то атрымаем (2). Даказана. ))
- найбольшыя хорды частковых мн-вау
і
то атрымаем (2). Даказана. ))
