21. Паняцце двайного інтэграла, геаметрычны сэнс.

Пусть

Опр.1: Число I наз. пределом интегральной суммы когда λ→0, когда ∀ε>0 ∃δ>0 | ∀T_p удовлетвор. Условию λ< δ и ∀(ε_k,γ_k) имеет место неравенство | - I |< ε.

Опр.2: Когда интегральная сумма при λ→0 имеет конечный предел =1 (2), который не зависит от способа разбивки мн-ва Р на частичные и от выбора точек (ε_k,γ_k) на част. мн-вах, то этот I наз. двойным интегралом функции f на мн-ве Р (интеграл Римана) и обозначается I= . Функ-я F наз. интегрируемой на мн-ве Р.

Г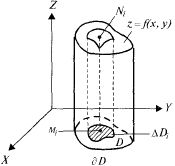 еометрический смысл.

Тело G ограничено сверху поверхностью

z= F(x;y), где F(x;y) – непрерывная, неограниченная на мн-ве Р функция, сбоку цилиндрической поверхности с направляющей параллельной оси OZ, снизу квадрируемой фигурой P в плоскости ОХY наз. цилиндрицеским брусом или телом.

Разложим мн-во Р на части Р_к, произвольным образом выберем точку (ε_k,γ_k). Рассмотрим ряд цилиндрических столбиков, которые имеют своими основаниями мн-ва Р_к, а

высшей f(ε_k,γ_k). Если каждый такой цилиндр. Столбик считать за цилиндр, то V каждого з них будет равный f(ε_k,γ_k)∙S(Р_к), где S(Р_к) – площадь каждой часть мн-ва Р_к. Тогда V(G)≈ .

Тогда, понятно, что дакладнае значение V можно получить, если перейти до предела в правой части равенства, когда λ→0:

V(G)= .

Отсюда следует геометрический смысл двойного интеграла: двойной интеграл от неадмоунай непрерывной на Р функции геометрически выражается объёмом соответствующего цилиндрического тела:

V(G)= (3)

22.Паняцце двайнога інтэграла, вылічэнне двайнога інтэграла паўторным інтэграваннем.

Паняцце двайнога інтэграла.

Разгледзем мноства і будзем лічыць, што мн-ва Р з’яуляецца квадравальнай фігурай, г. зн. мае плошчу. Вядома, што калі граніца фігуры з’яул. графікам непарыунай функцыі, то фігура квадравальная. Т. ч. мн-ва Р абмежаванае. Няхай на такім мн-ве Р вызначана функцыя дзвюх зменных: . Разаб’ем адвольным чынам вобласць Р сеткай крывых на канечную колькасць частак: , …, , …- частковых мноствау, плошчы якіх адпаведна роуныя: S( ), S( ), …, S( ),…. , …, - Т-разбіука мн-ва Р на частковыя мн-вы. Пры гэтым граніцы усіх маюць нулявую плошчу. Мн-ва не перасякаецца і разам са сваімі граніцамі даюць мн-ва Р з граніцай. На адвольным частковым мн-ве возьмем адвольны пункт ( , ) і саставім наступную суму:

, ) S( ). (1)

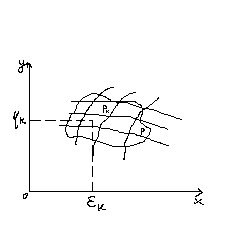Сума (1) называецца інтэгравальнай сумай ці сумай Рымана функцыі на мн-ве Р.

Дыяметрам замкнутага мн-ва Р назавем найбольшую адлегласць паміж двума пунктамі граніцы гытага мн-ва, ці найбольшую хорду мн-ва. Праз λ абазначым найбольшы з дыяметрау .

А зн.1 Лік Ј называецца lim інтэгральнай сумы , калі λ 0, калі на частковыя, падпарадкаванай умове λ<0 і пры ( , ) мае месца няроунасць: .

Азн.2 Калі інтэгральная сума пры λ 0, мае канечны lim Ј, г. зн. lim = Ј (2) пры λ 0 , які не залежыць ад спосаба разбіукі мн-ва Р на частковыя і ад выбару пунктау ( , ) на частковых мн-вах, то гэты lim Ј наз. Двайным інтэгралам функцыі на мн-ве Р.

Абазначаецца: Ј= .

Функцыя у гэтым выпадку наз. Інтэгравальнай на мн-ве Р.

Вылічэнне двайнога інтэграла. Прамавугольная вобласць.

Тэар.1 Калі для функцыі вызначанай у прамавугольніку Р=[a,b,c,d] (3) і пры адвольным пастаянным значэнні х з адрэзку аднакратны інтэграл (просты) (4), то пауторны інтэграл (5) і выконваецца роунасць : (6).

Доказ:

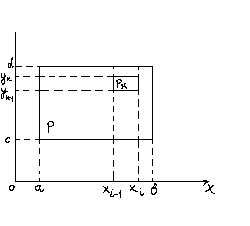Разаб’ем і [c,d] на часткі пунктамі: і , к (1,m). c

Тады прамавугольнік Р разаб’ецца на частковыя прамавугольнікі = .

Абазначым праз і адпаведна дакладную ніжнюю і дакладную верхнюю межы функцыі у прамавугольніку , тады выконваецца: .

Зафіксуем пункт х адвольным чынам на кожным частковым адрэзку. Няхай х= (зафіксуем) і праінтэгруем няроунасць у межах ад да .

, дзе .

Зауважым, што інтэграл па у будзе існаваць, т. як па умове існуе (4) на[c,d] .

Атрыманую няроунасць прасумуем па к, дзе кзмяняецца ад 1 да m.

.

Атрыманую няроунасць памножым на і прасумуем па і, дзе і .

Злева і справа будуць стаяць сумы Дарбу для інтэграла (3), пасярэдзіне – інтэгральная сума для функцыі . Т. ч. усе часткі імкнуцца да .

З другога боку (8).

З (7) , (8): =(4)= , а гэта (6).

Калі памяняць ролямі зменныя х і у, то, аналагічна, можна атрымаць формулу (6”):

пры умове, што пры пастаянным у

Заувага1. Калі разам з (3) існуюць два аднакратных (4) і (9), то формулы (6) і (6”) выконваюцца адначасова і .

Заувага 2. Калі вядома, што функцыя непарыуная, то вядома, што існуюць (3), (4),(9).І мы можам карыстацца любой з формул (6) і (6”) для (1).

Крывалінейная вобласць.

Разгледзем вобласць Р, абмежаваную зверху і знізу непарыунымі крывымі у= (х) і у= (х), а з бакоу – прамымі х= і х= . Тады мае месца тэарэма:

Тэар.2 Калі для функцыі , вызначанай у воблясці Р існуе (3) і пры кожным пастаянным значэнні х з аднакратны інтэграл: = , то будзе існаваць пауторны інтэграл:

(10).

Доказ:

Заключым вобласць у прамавугольнік R=[a,b,c,d] , дзе c=min (х), d=max (х), a<x<b. І у гэтым прамавугольніку разгледзем дапаможную функцыю:

(x,y)=

Функцыя інтэграв. на R, т. як на Р яна супадае з інтэграв. функцыяй , а на (x,y)=0, яна пастаянная і таксама ін6тэграв., прычым двайны інтэграл =0. Т. ч. мы атрымалі:

Даказана.

Зайвага1.Калі вобласць Р абмежавана крывымі х= (у) і х= (у), у=с, у= . То аналагічна можна атрымаць формулу (11):

. Пры умове існавання гэтага інтэграла і інтэграла пры пастпянным у з [c,d].

Азн. Стандартнай вобласцю у накірунку дадзенай восі наз. вобласць для якой любая прамая, паралельная гэтай восі, якая мае з вобласцю агульныя пункты, перасякае мяжу вобласці толькі у двух пунктах – пункце увахода і пункце выхаду.

Заувага2. Калі вобласць Р з’яул. стандартнай у накірунку Ох і Оу, то можна выкарыстоуваць і (10), і (11).

Заувага 3. Калі непарыуная на Р, то усе інтэгралы у (10), (11) абавязкова будуць існаваць і іх трэба выкарыстоуваць у залежнасці ад тыпу вобласці.

Заувага4. У выпадку нестандартнай вобласці Р, яна раскладаецца на канечны лік стандартных.