1.Паняцце функцыі многіх зменных. Узроўні функцыі многіх зменных

Разгл. некаторае падмноства D метрычнай прасторы R². Вядома, што R² — гэта мн—ва ўсемагчымых упарадкаваных пар (x;y).

Азн.1: Адпаведнасць f паміж мноствам D 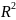 і мноствам R, пры якой для кожнай пары (x;y)є D вызначаецца адзіны лік zєR, называецца функцыяй 2-х незалежных зменных. Пішуць z=f(x,y). Мн—ва D наз. абсягам вызначэння ф—цыі f . x, y — незалежныя зменныя. Калі дадзены п—т (x₀;y₀)є D, то можна знайсці адпаведнае яму значэнне z₀ | z₀=f(x₀;y₀).

{z₀} наз. абсягам значэння ф—цыі.

Графікам ф—цыі наз. мн—ва п—таў (x, y, f(x,y)) є R³

Лініяй узроўню ф—цыі z=f(x;y), дзе (x;y)є D наз. мн—ва п—таў (x, y) є R², якія здавальняюць f(x,y)=с, сє R.

Азн 2: Графікам ф-цыі 2-х зменных z=f(x;y)| x;yє D наз.мн-ва п. (x, y, f(x,y)) є R³

Азн 3: Лініяй узроўню ф-цыі z=f(x,y), x;yє D наз.мн-ва п. (x, y) є R², якія здав.раўнанню f(x,y)=c, c нал.R

Азн 4. Адпаведнасць f паміж мноствам D  R^m , m > 1, m є Z і мноствам R, пры якой для кожнага пункта х = (х₁, х₂, …, х_m) є D вызначаны адзіны лік y є R называецца сапраўднай функцыяй m сапраўдных зменных, ці коратка – функцыя многіх зменных. Будзем пісаць у = f(x), дзе х – элемент з каард (х₁, х₂, …, х_m) є R^m. Можна абазначыць і так: у = f(х₁, х₂, …, х_m), x_i є R, 1 ≤ i ≤ m.

Пры гэтым D – абсяг вызначэння функцыі f; х₁, х₂, …, х_m – незалежныя зменныя.

Значэнне функцыі у₀ = f(х₁⁰, х₂⁰, …, х_m⁰) называецца значэннем функцыі f у пункце (х₁⁰, х₂⁰, …, х_m⁰). Мноства ўсіх такіх пунктаў у₀ ёсць мноства значэнняў функцыі многіх зменных.

Азн 5. Узроўнем функцыі f(х), дзе х є R^m называюць мноства пунктаў х є D  R^m, якія здавальняюць наступнаму раўнанню f(х) = с, с є R. Узроўні ф-цыі наз.паверхнямі ўзроўні: f(x,y,z)=c, c є R.

2.Ліміт функцыі дзвух зменных (ф.Д.З), непарыўнасць, раўнамерная непарыўнасць

Няхай дадзена функцыя z = f(x, y), (x,y) є R² (R² – мноства усемагчымых упарадкаваных пар (х, у)). Няхай М₀ (х₀,у₀) – лімітавы пункт D(f). Паслядоўнасць пунктаў (М_n) = M₁(x₁, y₁), M₂(x₂, y₂), …, M_n(x_n, y_n), … збягаецца да пункта М₀, калі адлегласць ρ(М_n, М₀)=0,калі n→∞.

Ці інакш: для збежнасці паслядоўнасці пунктаў (М_n) можна было б патрабаваць, каб паслядоўнасць каардынатаў (х_n) і (y_n), паслядоўнасць пунктаў (М_n) імкнуліся б адпаведна да пунктаў х₀,у₀. Г. зн., што х_n→х₀, у_n→у₀.

Няхай абсяг вызначэння D(f) змяшчае наваколле п—таў (x, y) є R² , акрамя можа быць самога (x₀;y₀).

Азн 1.(па Гейнэ): Лік А называюць лімітам функцыі f у пункце (х₀,у₀), ці пры ўмове х→х₀, у→у₀, калі для любой паслядоўнасці пунктаў (M_n(x_n, y_n)), якая збягаецца да пункта М₀(х₀,у₀) з членамі є D(f) і адметнымі ад пункта М₀, адпаведная паслядоўнасць значэнняў функцыі (f_n(x_n, y_n))=f(М_n) імкнецца да A.

А = lim f(x, y) ці f(x, y)→А, калі х→х₀, у→у₀

^{x → x}₀^{, y → y}₀

Азн 2.(па Кашы): Лік А называюць лімітам функцыі f у пункце (х₀,у₀), ці пры ўмове х→х₀, у→у₀, калі для любога ε > 0 існуе δ(ε) > 0 / V (x, y) ϵ D(f), 0< |x – x₀|< δ, 0<|y – y₀|<δ => | f(x, y) - А | < ε

Азн 3. Няхай функцыя z = f(x, y) вызначана ў лімітавым пункце М₀ (х₀,у₀) ϵ D(f) і некаторым яго наваколлі. Калі выконваецца ўмова lim f(x, y) = f(х₀,у₀)

^{x → x}₀^{, y → y}₀

функцыя f называецца непарыўнай у пункце (х₀,у₀).

Азн 3’. Функцыя f (x, y) называецца непарыўнай у пункце М₀(х₀,у₀), калі выконваецца ўмова lim ∆ f = 0, г. зн. бясконца малым прыростам аргумента

^{x → x}₀^{, y → y}₀

адпавядае бясконца малы прырост функцыі.

Тэарэма: Калі функцыя f непарыўна у п. М₀ не належыць D(f) па сукупнасці зменных, то яна непарыўна у гэтым пункце па кожнай са зменных. Г.зн. выконваецца

1) lim f(x, y₀) = f(х₀,у₀) ці 2) lim f(x₀, y) = f(х₀,у₀)

^{x → x}₀ ^{y → y}₀

Азн 4. Функцыя f называецца непарыўнай на мностве D є R², калі яна непарыўна у кожным пункце гэтага мноства. Калі функцыя не з’яўляецца непарыўнай у пункце М₀, то гавораць, што яна мае разрыў у пункце М₀.

Азн 5. Пункт М₀ назыв пунктам разрыва ф-ыі f, калі: 1) ф-ыя f нявызначана ў п. М₀, 2) ф-ыя f вызначана ў п. М₀, але lim f(x, y) не існуе ці існуе і lim f(x, y)≠ f(х₀,у₀)

^{x → x}₀^{, y → y}₀ ^{x → x}₀^{, y → y}₀

Азн 6. Функцыя z=f(x,y) назыв раўнамерна непарыўнай на мностве D є R², калі для любога ε > 0 існуе δ(ε) > 0 / V (x’, y’), (x”, y”) ϵ D, |x’ – x”|< δ,|y’ – y”|<δ

=> | f(x’, y’) - f(x”, y") | < ε