45. Уравнение , его общее и частные решения
- общее решение
дифференциального уравнения.
Зная общее решение однородного дифференциального уравнения и любое частное решение неоднородного уравнения, можно получить общее решение неоднородного уравнения в виде суммы общего решения однородного уравнения и частного решения неоднородного.
46. Понятие о средних. Среднее арифметическое, квадратичное, геометрическое, гармоническое и их определяющие свойства. Неравенства между средними.
Средней величиной называют показатель, который характеризует обобщенное значение признака или группы признаков в исследуемой совокупности.
Введем следующие
условные обозначения:
-
величины, для которых исчисляется
средняя;
-
средняя, где черта сверху свидетельствует
о том, что имеет место осреднение
индивидуальных значений;
-
частота (повторяемость индивидуальных
значений признака).
Различные средние
выводятся из общей формулы степенной
средней:
при
k = 1 - средняя арифметическая; k = -1 - средняя
гармоническая; k = 0 - средняя геометрическая;
k = -2 - средняя квадратическая.
Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Частоту f называют весом средней.
Средняя арифметическая
- самый распространенный вид средней.
Она используется, когда расчет
осуществляется по несгруппированным
статистическим данным, где нужно получить
среднее слагаемое. Средняя арифметическая
- это такое среднее значение признака,
при получении которого сохраняется
неизменным общий объем признака в
совокупности.Формула средней арифметической
(простой) имеет вид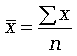
При расчете средних
величин отдельные значения признака,
который осредняется, могут повторяться,
поэтому расчет средней величины
производится по сгруппированным данным.
В этом случае речь идет об использовании
средней арифметической взвешенной,
которая имеет вид
Простая средняя
гармоническая используется тогда, когда
веса значений признака одинаковы. Ее
формулу можно вывести из базовой формулы,
подставив k = -1:
гармоническая
взвешенная:
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака (например, между 100 и 1000000). Существуют формулы для простой и взвешенной средней геометрической.
Для простой средней
геометрической
Для взвешенной
средней геометрической
Средняя квадратическая
величина. Основной сферой ее применения
является измерение вариации признака
в совокупности (расчет среднего
квадратического отклонения). Простая
средняя квадратическая:
Взвешенная
средняя квадратическая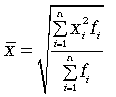
t-критерий Стьюдента - общее название для класса методов статистической проверки гипотез (статистических критериев), основанных на сравнении с распределением Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках.
В случае с
незначительно отличающимся размером
выборки применяется упрощённая формула
приближенных расчётов:
В случае, если
размер выборки отличается значительно,
применяется более сложная и точная
формула: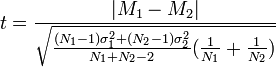
Где M1,M2 - средние
арифметические, σ1,σ2 - стандартные
отклонения, а N1,N2 - размеры выборок.Количество
степеней свободы рассчитывается как
Для вычисления
эмпирического значения t-критерия в
ситуации проверки гипотезы о различиях
между двумя зависимыми выборками
(например, двумя пробами одного и того
же теста с временным интервалом)
применяется следующая формула:
где Md - средняя разность значений, а σd - стандартное отклонение разностей.
Количество степеней
свободы рассчитывается как
Одновыборочный
t-критерий применяется для проверки
гипотезы об отличии среднего значения
от
некоторого известного значения
:
Количество степеней свободы рассчитывается как