1. Высказывание – утвердение , о котором можно сказать истинно оно или нет. (Напр.)Часто высказывание содержит переменную и значение истинности высказывания зависит от значения переменной.(Напр. Х – символ Нового года. Если Х_ Дед Мороз – истина, если Х-русалка – нет). Высказывания обозначают маленькими латинскими буквами. Некоторые простейшие высказывания с помощь логических связок можно представить как составные высказывания. Существует 4 типа операций над высказываниями:отрицание, логическое сложение («или»),логическое умножение(«и») и импликация. . Если высказывание р истинно, то пишут р = 1, если ложно, то используют запись р = 0.

1. Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания(обозначается ) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Записывается с помощью таблицы.

р р-

и л

л и

2. Логическое сложение(дизъюнкция). Объединение двух высказываний в одно с помощью союза «ИЛИ», употребляемого в неисключающем смысле, называется операцией логического сложения. Записывают pvq.Истинность преверяют благодаря такой таблицке

p q pvq Это высказывание истинно, когда хотябы 1 из p или q истинно.и ложно, когда p и q оба ложны.

и и и

л л л

и л и

л и и

3. Логическое умножение(конъюнкция).Записывают p^q. Если высказывание р истинно, то пишут р = 1, если ложно, то используют запись р = 0. Объединение двух высказываний в одно при помощи союза «И» называется операцией логического умножения. Проверяют истинность составляя табличку.

p q pиq Это высказ. истинно только тогда,когда истинно pиq одновр.

и и и

л л л

и л л

л и л

4. импликация (логическое следование.). Записывается p=>q, читается Если п, то ку. Выяснить истинность можно с помощью таблицы

p q p=>q Это высказывание ложно в единственном слчае:когда р истинно и при этом ку ложно

и и и

л л и

и л л

л и и

2. Операция логического отрицания осуществляется над одним высказыванием. Выполнить операцию логического отрицания (обозначается ) – значит получить из данного высказывания новое, присоединяя слова «неверно, что …» ко всему высказыванию. Записывается с помощью таблицы.

р р-

и л

л и

3. импликация (логическое следование.). Записывается p=>q, читается Если п, то ку. Выяснить истинность можно с помощью таблицы

p q p=>q Это высказывание ложно в единственном слчае:когда р истинно и при этом ку ложно

и и и

л л и

и л л

л и и

Суждение, выражаемое импликацией, выражается также следующими способами:

Посылка является условием, достаточным для выполнения следствия;

Следствие является условием, необходимым для истинности посылки.

теорема – матем.высказывание, вида если р, то ку назыв. Теоремой, при этом р – назыв условием, а ку – заключением теоремы. Существуют следующие виду теорем, если имеет место прямая теорема p=>q: 1.обратная теорема q=>p, 2.противоположная теорема p-=>q-,3.обратная противоположной.q- =>p-. Истинность теоремы p=>q не влечет истинность обратной теоремы q=>p.

Доказательство от противного состоит в том, что вместо прямой теоремы доказывается равнозначная ей q- =>p-. Т.е. предполагаем, что заключение теоремы неверно и доказывываем, что тогда неверно и условие.

Пусть имеет место теор. p=>q(т.е.всякий раз, когда истинно р, истинно и ку) В таком случае говорт, что для р является достаточным условием для ку, а ку – есть условие необходимое для р.

Суждение K является необходимым и достаточным условием суждения X, когда K является как необходимым условием X, так и достаточным. В этом случае говорят ещё что K и X равносильны, или эквивалентны.

Для суждений X типа «объект принадлежит классу M» такое суждение K называется критерием принадлежности классу M.

4. Множество – совокупность элементов, обладающих отличительными особенностями. Для обозначения множеств используют большие лат.буквы, а элементы множеств- мал.лат.буквами.Например, запись аєА обозначает, что а принадлежит множеству А. вє\А – в не принадлежит мн.А. существует несколько вариантов задания множеств. 1. перечислением элементов. (А={5;7;8}), 2. свойством, отличающим элементы элементы множества от всех других. (В={xє|R|x2>1}). Мноество В содержится в мн.В, если любой элемент мн.А, явл.элементом мн.В. записывается так: АсВ). Два мн.назыв.равными(А=В), если АсВ, ВсА. Т.е. хєАхєВ.(изобр.2 мн.).

Основніе операции над мн. 1. Объединение. это множество содержащее все элементы множества А, так и все э-ты мн.В. Если множества A и B не пересекаются: , то их объединение обозначают также: . 2. пересечение: это мн., содержащее все эл-ты общие для А и В. 3. дополнение мн-а: А:А- . А- ={хєU\ хє/А}. Єто мн.всех єлементов, не принадлежащих А. Множества связаны с логическими операціями след.оразом: 1.если мн.А задано свойством р, то дополнение А- задано свойством р-(отрицание р). 2. если мн.А задано св-м р, а мн.В – св.ку, то объединение АUВ задается логич.суммой р или ку, пересечение А и В( АЛВ) задается логическим умножением р и ку. 3. если АсВ(А подмножество В), то справедлива импликация p=>q.

5. Ква́нтор — общее название для логических операций, ограничивающих область истинности какого-либо предиката. Чаще всего упоминают:

Квантор всеобщности (обозначение: , читается: «для всех…», «для каждого…» или «каждый…», «любой…», «для любого…») и Квантор существования (обозначение: , читается: «существует…» или «найдётся…»). С пом.таких кванторов можно записывать высказывания(среди студентов есть отличники( ст:ст=отл), все вороны черные ( ворона: ворона явл.черной).

Структура записи высказываний: (квантор.высказывание): (осн.логич.утверж.). Но кванторы различного смысла менять местами нельзя, т.к. получится другое высказывание, а кванторы одинакового смысла менять местами можно и даже можно объединять.

Построение отрицаний. Квантор заменяется на двойственный ( -> ; -> ), описание сохраняется, а осн.логич.утвержд тоже заменяется отрицанием. ( ст:ст=отл. ст:=/отл – нет отличников.)

6. Прямая с выбранным на ней началом отсчета, единичным отрезком и направлением называется координатной прямой. Число, показывающее положение точки на прямой, называют координатой этой точки

Расстояние |AB| между точками A(x₁) и B(x₂) на прямой: |AB|=

Если точка М(x) лежит на прямой, проходящей через две данные точки

( ) и ( ), и дано отношение , в котором точка М делит отрезок , то координата точки М определяется по формуле ,.

Если точка М является серединой отрезка , то ее координата определяется по формуле .

7. Координаты точки записываются в скобках рядом с названием точки, причем всегда на первом месте в прямоугольной системе координат записывается абсцисса точки, а на втором - ее ордината. Например, если x₁ - абсцисса точки A, а y₁ - ее ордината, то это записывается так: A(x₁, y₁).

У точки, лежащей на оси абсцисс, ордината равна нулю; у точки, лежащей на оси ординат, абсцисса равна нулю. Обе координаты начала координат равны нулю.

Расстояние |AB| между точками A(x₁, y₁) и B(x₂, y₂) плоскости определяется по формуле: |АВ|=

Если точка М(x; y) лежит на прямой, проходящей через две данные точки ( , ) и ( , ), и дано отношение , в котором точка М делит отрезок , то координаты точки М определяются по формулам , .

Если точка М является серединой отрезка , то ее координаты определяются по формулам , .

8. графиком уравнения F(x;y)=0 назыв.множество точек плоскости с координатами (x;y), которые удовлетворяют этому ур-ю: F={(x;y)є|R2:F(x;y)=0} (y-х=0- ур-е=>у=х- его график – прямая, которая является биссектрисой 1 и 111 координатной четверти).

Важный класс линий составляют те, для которых функция F(x,y) есть многочлен от двух переменных, в этом случае линия, определяемая уравнением F(x,y)=0, называется алгебраической. Алгебраические линии, задаваемые уравнением первой степени, прямые. Уравнение второй степени, имеющее бесконечное множество решений, определяет эллипс, гиперболу, параболу или линию, распадающуюся на две прямые.

График функции — множество точек, у которых абсциссы являются допустимыми значениями аргумента x, а ординаты — соответствующими значениями функции y.

Пусть на плоскости задана некая линия L(множество точек). Уравнение линии L назыв.такое уравнение вида F(x;y)=0, что координаты любой точки множ. L удовлетворяют этому уравнению: М(х;у)єL=>F(x;y)=0

Прямая линия - график линейной функции y = ax + b. Функция y монотонно возрастает при a > 0 и убывает при a < 0. При b = 0 прямая линия проходит через начало координат т. 0 (y = ax - прямая пропорциональность).

Общее уравнение прямой имеет такой вид ах+ву=с.

Уравнеие окружности - множество точек М с координатами (х;у), которые находятся от центра О(0;0) на расстоянии R, т. М(х;у) и т. О(0;0). Уравнение ок-ти находят по формуле (x-x_o)² + (y-y_o)² = R² ур-е окружности с центром в т. А(х0,у0) и радиусом R.

9. общее ур-е прямой ах+ву=с в зависимости от коэффициентов а и в можно записать след.образом:

1.а=0=>y=d (d- какое-то число). Ее график – горизонтальная прямая, проходящая через точку (0,d).

2. в=0=> x=d – вертикальная прямая проходящая через точку (d,0).

3. а=/0, в=/0=>y=kx+d – наклонная прямая(если k =/0)

Угловой коэффициент прямой y=kx+d – это k. Его геометрический смысл – тангенс угла наклона прямой,т.е. тангенс угла, который прямая образует с положительным направлением оси Х. d-свободный член управления и его геометрический смысл – ордината точки пересечения прямой с осью У.

Уравнение прямой, проходящей через т.А (х0,у0) и угловым коэффициентом k имеет такой вид: y-y0=k(x-x0).

Условие параллельности прямых. Если прямые(y=kx+b1 и y=k2x+b2) заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k₁ = k₂.   

Условие перпендикулярности. В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку. Т.е.k=-1/k1(или k1k2=-1).

10. Пусть на плоскости заданы две точки M₁(x₁, y₁) и M₂(x_2, y₂), тогда уравнение прямой, проходящей через эти точки:                                        

Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

Дробь = k называется угловым коэффициентом прямой.

11. вектор- направленный отрезок прямой. Н-мерным вектором назыв.набор из н-чисел. а->=(а1;а2;…;ан). Для н-мерных векторов можно определить операции сложения векторов и умножения вектора на число покоординатно:а-=(а1,а2,…,ан); в-=(в1,в2,…,вн); а- +в-=(а1+в;а2+в2;…;ан+вн). Ka-=(ka1;ka2;…;kan), к – некоторое число.

В декартовой системе координат вектор может быть задан двумя числами: и

Эти числа и в геометрии называют координатами вектора, а в физике – проекциями вектора на соответствующие оси координат. При таком определении вектора его модуль , а направление задается углом , который однозначно определяется соотношениями: и .

Суммой векторов и называют вектор , идущий из начала вектора в конец век­тора при условии, что начало вектора приложено к концу вектора . Координаты вектора суммы двух векторов удовлетворяют соотношениям: и

Вектор суммы двух векторов:

Произве­дением  вектора на число  называют вектор, коллинеарный вектору , имею­щий длину, равную , и направле­ние, совпадающее с направлением при > 0 и противоположное при < 0.

Координаты вектора произведения вектора на число удовлетворяют соотношениям:

Произведение вектора на число:

Операции сложения векторов и умножения вектора на число обладают след. свойствами:

1) ,

2) ,

3) ,

4) ,

5) ,

6) ,

7) ,

8) .

Пусть а1-,а2-,…,ан- векторы. с1,с2,…,сн – числа. Линейной комбинацией а1-, а2-,…,ан- векторов назыв.вектор b- =c1a1-+c2a2-+…+cнан-, при этом числа с1, с2,…,сн – назыв коэффициентами линейной комбинации.

Линейно-независимой системой векторов назыв.такая система векторов …, что из того, что линейная комбинация этих векторов равна 0 следует, что все коэффициенты этой линейной комбинации равны 0, т.е. c1a1-+c2a2-+…+cнан- =0- =>с1=с2=..=сн=0.

В противном случае, система векторов назыв линейно-зависимой, если существуют коэффициенты с1, с2…,сн не все равные 0. также, что линейная комбинация c1a1-+c2a2-+…+cнан- = 0-. Если система векторов линейно-зависима, то хотя бы один из векторов этой системы линейно выражается через остальные . т.е. один вектор является линейной комбинацией остальных векторов.

Если же система векторов линейно независима, то ни один вектор системы линейно не выражается через остальные.

Базисом линейного пространства назыв.максимальная линейно независимая система векторов, т.е. такая система векторов а1-, а2-,а3-, ..,ан-.: 1. сама система векторов а1-,а2-,…, ан- Линейно независима.2. если к этой системе добавить еще хотя бы один вектор, то получится уже линейно зависимая система.

12. Матрица- прямоугольная таблица чисел, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.транспонированной по отношению к матрице А назыв матрица Ат, у которо стороны и столбцы матрицы А поменяны местами. Квадратной назыв.матрица, у которой число строк равно числу столбцов.это число назыв.порядкоа матрицы.главной диагональю квадратной матрицы назыв.элементы а11,а22,а33,…,анн, а боковой диагональю назыв элементы а1н, а2(н-1)…,ан1.

Диагональной назыв.матрица, у которой все элменты, кроме главной диагонали равны 0.

Треугольной назыв матрица, у которой элементы над(или под) главной диагональю равны 0.

Матрицы допускают следующие алгебраические операции: сложение матриц, имеющих один и тот же размер;умножение матриц подходящего размера (количество строк одной матрицы должно совпадать с количеством столбцов другой);умножение матрицы на элемент основного кольца или поля (т. н. скаляр). Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют векторное поле над соответствующим кольцом или полем. Для квадратных матриц матричное умножение является замкнутой операцией, поэтому квадратные матрицы одного размера образуют кольцо относительно матричного сложения и матричного умножения.

Умножение матрицы A на число λ (обозначение: λA) заключается в построении матрицы B, элементы которой получены путём умножения каждого элемента матрицы A на это число, то есть каждый элемент матрицы B равен b_ij = λa_ij

Сложение матриц A + B есть операция нахождения матрицы C, все элементы которой равны попарной сумме всех соответствующих элементов матриц A и B, то есть каждый элемент матрицы C равен c_ij = a_ij + b_ij

Умножение матрицы на вектор производится по правилу «строка на столбец». Для возможности такого умножения длинна строки матрицы должна быть равно длинне вектора, который в этом случае записывают как вектор-столбец.

Умножение матрицы на матрицу – по правилу «строка на столбец.». для возможности такого умножения матрицы А на матрицу В нужно, чтобы длинна строки(т.е. к-во столбцов) матрицы А была равна длине столбца (т.к. к-ву строк) матрицы В.

13. каждой квадратной матрице А можно сопоставить число называемое ее отпределителем или детерминантой.если А=(aij), то определитель матрицы А означаем detA=|aij| и вычисляется в зависимости от порядка н-матрицы.

Определитель второго порядка равен разности между произведениями элементов, лежащих на главной и побочной диагоналях.

Свойства определителей второго порядка:

1. Определитель не изменится, если его строки поменять местами с соответствующими столбцами.

2. При перестановке двух строк (или столбцов) определитель изменит знак на противоположный, сохраняя абсолютную величину

3. Определитель с двумя одинаковыми строками и столбцами равен нулю.

4. Общий множитель всех элементов строки или столбца можно выносить за знак определителя; если все элементы какой-то строки или столбца равны 0, то и определитель равен 0.

5. Если к элементам какой либо строки (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель не изменит своей величины.

Условие: определитель равен нулю тогда и только тогда, когда его строки или столбцы линейно зависимы.

14. Пусть дана квадратная таблица из девяти чисел , , , , , , , , :

. (1)

Определителем третьего порядка, соответствующим таблице (1), называется число, обозначаемое символом

и определяемое равенством

.

Для квадратной матрицы третьего порядка формула вычисления определителя разложением по 1-ой строке имеет вид:

detA= =(-1)1+1 x +(-1)1+2 x +(-1)1+3 x

По второму столбцу:

detA=|a11 a12 a13(a21 a22 a23)(a31 a32 a33)|=(-1)1+2x a12|a21 a23(a31 a33)|+(-1)2+2 x a22|a11 a13(a31 a33)|+(-1)3+2 x a32|a11 13(a21 a23)|=-a12(a21xa33-a23xa31)+a22(a11xa33-a13xa31)-a32(a11xa23-a13xa21)=(a12x a23x a31+a22x a11x a33+a32x a13x a21)-(a12x a21x a33+a22x a13x a31+a32xa11xa23).

По правилу треугольника сначала перемножаются и складываются элементы, соединенными на схеме линиями

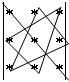
т.е. получаем сумму произведений: a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂.

Затем перемножаются и складываются элементы, соединенные на схеме

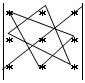
т.е. получаем другую сумму произведений a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂. И, наконец, чтобы вычислить определитель, из первой суммы вычитают вторую. Тогда окончательно получаем формулу вычисления определителя третьего порядка:

detA=(a₁₁a₂₂a₃₃+a₁₂a₂₃a₃₁+a₂₁a₁₃a₃₂)-(a₁₃a₂₂a₃₁+a₁₂a₂₁a₃₃+a₁₁a₂₃a₃₂).

15.пусть есть система из н-линейных уравнений с к-неизвестными(Напр.н=к=3), три линейных уравнения и три неизвестных.

{a11x+a12y+a13z=b1(a21x+a22y+a23z=b2)(a31x+a32y+a33z=b3)

Такая система назыв.однородной, если правая часть b1=b2=b3=0(т.е. b1(b2)(b3)=0-= 0(0)(0).

Система назыв.неаоднородной, если b->=/0->

Такой системе сопоставлют матрицу А=(стандартная 3х квадратная матрица.), которая назыв матрицей системы, а ее определитель – определителем системы и обозначается Δ (дельта). Δ =detA.

Прав.Крамера:

1)если Δ=/0, то система имеет единственное решение:

Х= Δх/Δ. У= Δу/Δ. Z= Δz/Δ.(т.е. система определена).

2) если Δ=0, а Δх, Δу, Δz=/0, то система несовместна, т.е. нет решений.

3)Если Δ=0, Δх= Δу= Δz=0, то система имеет бесконечно много решений, т.е. система неопределенна. Чтобы это решение найти. Нужно отбросить лишнее ур-е. лишние переменные перенести в правую часть и решать систему меньшего кол-ва ур-й относительно меньшего числа неизвестных.

16.метод Гаусса назыв.еще методом полного исключения и состоит он в том. Что вначале исключая неизвестные из последнего уравнения преводят систему к треугольному виду(прямой ход). А затем, исключая переменные «обратным ходом» приводят систему к диагональному виду.

Например.{2x-4y=6(3x+5y=1).1. прямой ход. 1е ур-е делят на 2=>{x-2y=3(3x+5y=1). Затем 1е ур-е умножают на (-3)=> {-3+6у=-9 (3х+5у=1)=>1+2=>{x-2y=3 (1+y=-8)/ далее 2е делим на 11=> {x-2y=3 (y= -8/11).

Обратный ход.

2е ур-е умнож на 2=> {x-2y=3 (2y=-16/11=> 1+2=> {x=17/11 (y=-8/11).

Ответ(17/11;-8/11).

17. Числовая ось, или числовая прямая — это прямая, на которой выбраны:

некоторая точка O — начало отсчёта;положительное направление, указанное стрелкой;

масштаб для измерения длин.

Между вещественными числами и числовой осью устанавливается взаимно однозначное соответствие: начало координат соответствует нулю, числовое значение произвольной точки соответствует расстоянию её до начала координат — в положительном направлении со знаком плюс, иначе — со знаком минус.[1] Таким образом, числовая ось состоит из точки начала координат и двух расходящихся от неё лучей, один из которых соответствует положительным, а другой — отрицательным числам. Естественный порядок точек на прямой при таком соответствии согласуется с упорядоченностью чисел.

Числовая прямая часто используется как наглядный образ множества вещественных чисел (например, для построения графиков). Отрезки прямой при этом изображают числовые интервалы.

Модулем неотрицательного действительного числа a называют само это число:

|а| = а

Модулем отрицательного действительного числа х называют противоположное число:

|а| = - а

Короче это записывают так:

Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки А(а).

|а·b| = |а| · |b|

Модуль числа не может быть отрицательным. Для положительного числа и нуля он равен самому числу, а для отрицательного – противоположному числу. Противоположные числа имеют равные модули:

|-а| = |а|

Модуль числа 0 равен 0, так как точка с координатой 0 совпадает с началом отсчета 0, т.е. удалена от нее на 0 единичных отрезков:

|0| = 0

На практике используют различные свойства модулей:

|а·b| = |а| · |b|

|а| = | - а|

|а + b| = |а| + |b|

|а·q| = q·|а| , где q - положительное число

.

Значение |a - b|  равно расстоянию на числовой прямой между точками, изображающими числа a и b.

Нера́венство треуго́льника утверждает, что длина любой стороны треугольника всегда не превосходит сумму длин двух его других сторон.

Пусть дан треугольник ΔABC. Тогда причём равенство | AC | = | AB | + | BC | достигается только тогда, когда треугольник вырожден, и точка B лежит строго между A и C.

18. функцией назыв. такое соответствие между двумя множествами ХиУ, при котором каждому элементу хєХ ставится в соответствие единственное значение єлемента уєУ. Этот факт записывается символом : у=f(x).Функцию моно задать формулой(у=2х+3) и таблицей.

Множество Х назыв.областью определенияфункции и обозначают Д(у), а множество У назыв. множеством значений ф-ции и обозначают Е(у)..

Функция называется четной, если при всех значений  из области определения этой функции .

Функция называется нечетной, если при всех значений  из области определения этой функции .

Область определения четной и нечетной функции симметрична относительно начала координат.

Функция  называется возрастающей (убывающей) на данном промежутке, если при произвольных двух различных значениях аргумента, из данного промежутка, большему значению аргумента соответствует большее (меньшее) значение функции.

Функция  называется периодической, с периодом , где , если значение функции не изменяется при прибавлении числа  к любому допустимому значению аргумента: .

Функция  называется ограниченной, если можно указать такое положительное число , что  для всех значений  из области определения функции. Если же точка  не существует, то функция называется неограниченной.

Графиком функции  называется множество всех точек плоскости, координаты которых .

Осн.элементарныйе ф-ции.

1. линейная ф-ция. Ее график – прямая y=kx+b

2. квадратичная ф.ее график – парабола. Y=ax2+bx+c(a=/0). Если а >0 – ветви вверх, если а<0 –ветви вниз.координаты вершин параболы:xb=-b/2a, yb=y(xb). (y=x2-3x+1 (3/2;-5/4)

3. степенная ф. у=х*н ее вид зависит от различных н.

4. показательная ф. y=a^x(a>0,a=/1)

5. логарифмическая ф. Y=log_a x(a>0,a=/1, x>0)

6. тригонометрические ф. у=sinx, y=cosx,y=tgx,y=ctgx

19. Преобразования графиков функций — термин, используемый в школьной программе для обозначения линейных преобразований функции или её аргумента вида y = αf(γx + δ) + β. Применяется также для обозначений операций с использованием модуля.

Общий вид функции	Преобразования
y = f(x − a)	Параллельный перенос графика вдоль оси абсцисс на | a | единиц вправо, если a > 0; влево, если a < 0.
y = f(x) + a	Параллельный перенос графика вдоль оси ординат на | a | единиц вверх, если a > 0, вниз, если a < 0.
y = f( − x)	Симметричное отражение графика относительно оси ординат.
y = − f(x)	Симметричное отражение графика относительно оси абсцисс.
y = f(kx)	При k > 1 — сжатие графика к оси ординат в k раз, при 0 < k < 1 — растяжение графика от оси ординат в 1 / k раз.
y = kf(x)	При k > 1 — растяжение графика от оси абсцисс в k раз, при 0 < k < 1 — cжатие графика к оси абсцисс в 1 / k раз.
y = | f(x) |	При — график остаётся без изменений, при f(x) < 0 — график симметрично отражается относительно оси абсцисс.
y = f( | x | )	При — график остаётся без изменений, при x < 0 — график симметрично отражается относительно оси ординат.

20. Последовательность — это набор элементов некоторого множества:

для каждого натурального числа можно указать элемент данного множества;

это число является номером элемента и обозначает позицию данного элемента в последовательности;

для любого элемента (члена) последовательности можно указать следующий за ним элемент последовательности.

Таким образом, последовательность оказывается результатом последовательного выбора элементов заданного множества. И, если любой набор элементов является конечным, и говорят о выборке конечного объёма, то последовательность оказывается выборкой бесконечного объёма.

Пусть задано некоторое множество X элементов произвольной природы.

Всякое отображение из множества натуральных чисел в заданное множество X называется последовательностью (элементов множества X).

Образ натурального числа n, а именно, элемент xn = f(n), называется n-ым членом или элементом последовательности, а порядковый номер члена последовательности — её индексом.

Последовательности вида

принято компактно записывать при помощи круглых скобок: (xn) или

иногда используются фигурные скобки:

Допуская некоторую вольность речи, можно рассматривать и конечные последовательности вида ,

которые представляют собой образ начального отрезка последовательности натуральных чисел.

Примеры:

Целочисленная последовательность

Функциональная последовательность где

21. Определение придела:Число А назыв.приделом переменной величины д в процессе П(пушут limal=А)если для любого сколько угодно малого числа ε>0 в процессе П наступит такой момент П0, после которого неравенство |A-al|< ε становится и остается справедливым.

Число a называется пределом последовательности {xn}, если для каждого ε > 0 существует такой номер Nε, что для всех n ≥ Nε выполняется неравенство |xn – a| < ε

т. е. При этом пишут, что или при n → ∞. Кратко это определение можно записать так:

Интервал (a – ε; a + ε) называют ε-окрестностью точки a.

Проще говоря, число a называется пределом последовательности {xn}, если в любой ε-окрестности точки a лежат все члены последовательности {xn},

изменение конечного числа членов последовательности не влияет ни на факт существования предела, ни на величину последнего.

Бесконечно малая (величина) — числовая функция или последовательность, которая стремится к нулю.

Значение А называется пределом (предельным значением) функции в точке , если для любого наперёд взятого положительного числа найдётся отвечающее ему положительное число такое, что для всех аргументов , удовлетворяющих условию , выполняется неравенство

Функция у=f(х) назівается бесконечно малой при х→x0,если .

Последовательность - ф-ция натурального аргумента, т.е. X=|N. В этом случае натуральный элемент обычно обозначают n, а значение ф-ции x_n,y_n.(x_n= 1/n, y_n=2^n).

22. Бесконечно большая (величина) — числовая функция или последовательность, которая стремится к бесконечности определённого знака.

Последовательность an называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки x0, если .

Функция называется бесконечно большой на бесконечности, если либо .

23. 1. limc=c,где с=const; 2. если lim al=A,lim lb=B,то lim(al+lb)=lim al+lim lb. lim (alxlb)=AxB. Lim(al/lb)=A/B(B=/0). 3. если al-бесконечно малая величина(limal=0), то величина 1/al-бесконечно больншая(lim 1/al=_8). 4. если lb- бесконечно большая величина, то 1/lb-бесконечно маленькая величина. 5. произведение органичений и бесконечно малой величины – бесконечно малая величина.

24.1.пусть al и lb – бесконечно малые величины, т.е.lim al=0 и lim lb=0. часто возникает вопрос, какая из этих величин быстрее стримится к 0. Чтобы это выяснить нужно рассмотреть отношение al/lb.

2. две бесконечно малые величины имеют одинаковый порядок малости, если lim al/lb=k=/0. в этом случае обозначают al=_O(al). В частности если lim al/lb=1, то бесконечно малые величины al и lb назыв.эквивалентными( ).

3. если придел отношения lim al/lb=0, то говорят, что бесконечно малая величина al имеет более высокий порядок малости по сравнению с бесконечно с бесконечно малой величиной lb(т.е. al быстрее стремится к 0, чем lb) пишут al=o-(lb).

4. al есть главная часть lb , если lb=al+o-(al). Для этого необходимо и достаточно, чтобы lim al/lb=1,т.е.

Al(х) и lb (х) – одного порядка малости при х->0(т.е Ал(х) и Бт(х) одинаково быстро стремятся к 0.

Сравнение роста ф-ций.

1.Можно даказыть, что при х->+_8 показательная ф-ция растет быстрее степенной.

2. lim(x->+_8) lnx(x^p)=0(p>0), т.е. при х->+_8 степенная ф-ция растет быстрее логарифмической. При этом lnx<<x^p(внизу х->+_8)<<a^x(p>0,>1)

Графически это можно продемонстрировать так:

25. производная характеризирует скорость изменения ф-ции. Изучая изменение некоторой величины Ал вводят понятие «приращения»: если было значении Ал0, а стало значение Ал, то приращение вел-ны это (Ал-Ал0)=/\Ал..

При изучении изменения ф-ции y=f(x) рассматривается приращение аргумента /\х=х-х0 (откуда х=х0+/\х) и приращение ф-ции /\у= /\f=f(x0+/\x)-f(x0). Для непрерывной ф-ции у=ф(х) в т.х0 выполняется следующее: lim(/\x->0) /\f= lim /\x->0[f(x0+/\x)-f(x0)]=lim(/\x->0[f(x0) – f(x0)]=0.

Производной ф-ции f(x) в т.х0 назыв.предел отношения приращения ф-ции к приращению аргемента. Обозначается у`(x)

Y`(x) =f`(x)= lim(/\x->0 /\f2//\x=lim f(x=/\x)-f(x)//\x.

Физический смысл.

1. пусть точка движется прямолинейно и S(t) – путь пройденный ею за время t. Vср.= /\S//\t, где /\S –разность путей во времени = S(t+/\t)-S(t).

Если точка движется неравномерно, то для точной х-ки движения этой точки будем уменьшать интервал времени(/\t->0), за которое изменилась скорость средняя и прийдем к монятию мгновенная скорость в момент t.

Lim(/\t->0) /\S/ /\t= S`(t) = V(t).

2.изучая изменения скорости на неком промежутке времени придем к понятию среднего ускорения.

Acp=/\V/ /\t=V(t+/\t) – V(t)/ /\t => a(t)= lim(/\t->0 /\V/ /\t=V`(t) – ускорение – производная скорости по времени.

3.плотность «Ро». Пусть есть материальная пластина длинны l и массы М. тогда средняя плотность пластины: Ро ср=/\M/ /\l

Если /\l->0, то Ро(l)=lim /\t->0 /\M//\l=M`(l). – линейная плотность пластины есть производная массы по длинне пластины.

4. сила тока І . пусть есть проводник и Q(t)- кол-во электричества проходящего через поперечное сечение проводника за время t. Тогда ср.сила тока на пром-ке (t, t+/\t): Iср=/\Q(t+/\t)-Q(t)/ /\t. Если t->0, то I(t)=lim(/\t->0 ) /\Q/ /\t=Q`(t) – сила тока – производная кол-ва электричества, проходящего через поперечное сечение проводника, за время t.

Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точки x₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную (постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

26.

27. Производная константы:

Производная суммы:

Произодная произведения:

Производная отношения:

Производная композиции: Если функция   имеет производную  , а функция   -- производную  , то композиция  )сложная функция) имеет производную

28. Дифференциал ф-ции y=f(x) в т. Ч назыв.главная линейная часть ее приращения, т.е. если f(x+/\ x)-f(x)=A/\x+o-(/\x), то линейная ф-ция A/\х независимой переменной /\х есть дифференциалом ф-ции y=f(x)в т.х. обозначается df(x)=A/\x.

df(x)=f`(x)dx – формула дифференциала ф-ции в т.х

Правило нахождения дифференциала ф-ции такжие же как и правила нахождения производной:

а) ;

б) ;

в) ;

г) ;

д) df(u)=f `(u) du – инвариантность первого дифференциала.

Применение дифференциала для приближенных вычислений. Если в определении дифференциала f(x+/\x) – f(x)= f ` (x)/\x+o-(/\x),отбросить о-(/\х), то получим приближенное равенство левой и правой части:

1. f(x+/\x) ~~f(x)+f ` (x)/\x.

2. f(x+/\x)~~f(x), при этом f ` /\x~~погрешность /\.

3. линеаризация ф-ции, т.е.приближенная замена ф-ции у=ф(х) в окресности точки х0 линейной ф-ции. f(x)~~f(x0)+f ` (x0)(x-x0) при x->x0

Формула Тейлора.

Формулу f(x)~~f(x0)+f ` (x0)(x-x0) можно обобщить используя производные высших порядков. Так, если в точке х0 существуют все производные до порядка n включительно, то справедлива формула Тейлора f(x)=f(x0)+f ` (x0)(x-x0)+f ``(x0)/2! (x-x0)2+f ```(x0)/ 3! (x-x0)3+…+f^n(x0)/n! (x-x0)^n+o-(x-x0)^n = Σот к=0 до n f^k(x0)/k! (x-x0)^k+o-(x-x0)^n.

29. Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

  Если подставить в эту формулу выражение

то получим приближенную формулу:

30. Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательно, либо всегда неположительно. Если в дополнение приращение не равно нулю, то функция называется стро́го моното́нной.

Достаточное условии монотонности ф-ции у=ф(х) на промежутке: если на промежутке (а,в) существует производная ф`(х) и эта производная f `(x)>0 для всех хє(а,в), то ф-ция ф(х) возрастает)стрелка вверх), а если f ` (x)<0 для все хє(а,в), то ф-ция ф(х) убівакт(стрелка вниз) на промежутке (а,в)

31. пусть т.х0є(а,в) из Д(у). т. х0 – точка локального внутрннего максимума, если существует такой інтервал (х0-б,х0+б), что для всех х из этого интервала f(x)<f(x0) (x=/x0) и точкой локальной внутр. Минимума назыв. если f(x)>f(x0) (x=/x0) нарисуй какую-то хрень с мин и макс.

Необходимое условие.

Если в т. х0 ф-ци имеет локальный внутр экстремум, то производная f `(x0)в этой точке или равно 0, или не существует, т.е. экстремум может быть только в тех точках х0, где f `(x0)=0 или f `` (x0) – не существует. Точки х0, в которых f `(x)=0 назыв стационарными, а точки , в которых f ` (х0)-не существуют – назыв. критическими.

Достаточное условие.

Если в самой т.х0 ф-ция непрерывна и при переходе черех эту точку в направлении возрастания Х.

А)f `(x) меняет знак с «+» «на «-», то в т. х0-макс

Б) f ` (x) меняет знак с «-« на «+», то в тю х0-мин.

В) f ` (x) не меняет знак, то в т. х0 нет экстремума; Обычно такое исследование проводят с помощью таблицы.

32. ф-ция назыв.выпуклой вверх на промежуьке(а,в), если любая ее хордана этом промежутке лебит ниже части графика, а выпуклой вниз, если наоборот- любая хорда лежит выше дуги графика.

Достаточное условие выпуклости ф-ции на промежутке:

Если вторая производная f ``(x)>0 для хє(а,в), то ф-ция ф(х) віпуклая вниз на єтом промежутке, если же f ``(x)<0 для хє(а,в), то ф(х) выпукла вверх на єтом промежутке.

Точка из области определения, в ккоторой меняется выруклость, назыв.перегибом.

33. схема:

1. єлементарніе свойства(обл..определения Д(у), область значения Е(у), четность, периодичность, точки пересечения с осями координат, промежутки знакопостоянства).

2. непрерывность и поведение ф-ции на границе области определения.

3. монотонность и экстремумы(с помощью первой производной)

4. выпуклость(с пом.второй производной).

Y=e^-x2 – кривая Гаусса.

1. 1.Д(у): хє(-_8,+_8)

2.у(-х-)= е^-(-x)2=e^-x2=y(x)- ф-ция четная=> график симметричен относительно Оу.

3.непериодична

4. с Ох: у=0=>e^-x2=0, x

34.ф-цию 2х переменных записывают в виде z=f(x;y), где (х,у) – это аргумент, а z –значение ф-ции.графиком ф-ции 2х переменных z=f(x;y) является поверхность в трехмерном пространставе.

Ф-цию 3х переменных можно записать так : u=f(x;y;z). Где и – зависимая переменная.

Для ф-ции нескольких переменных вводят понятие частных производных. Частной производной по х ф-ции 2х переменных ф(х,у) назыв.производная по х при фиксированном у. обозначается f `(x;y) или дf(x;y)/дх.

Частной производной по у ф-ции 2х переменных ф(х,у) назыв. производная по у при фиксированном х. обозначается f `у или дf(x;y)/ду.

Дифференциал ф-ции нескольких переменных – главная линейная часть приращения ф-ции.

Экстремум ф-ции нескольких переменных опредеяется также как и экстремум ф-ции одной переменной. Необходимое условии экстремума: если ф-ция нескольких переменных имеет в некоторой точке(х0,у0) локальный внутренний экстремум, то все ее частные производные равны 0,т.е. f `x(x0,y0)=0 и f ` y(x0,y0)=0( (x0,y0)- стационарная точка). Если известно, что у ф-ции ф(х,у) есть экстремум и есть только одна стационарная точка (х0.у0), то эта точка и является точкой экстремума.

35.эмпирической называют формулу, полученную в результате эмпирического эксперимента. Пусть в некотором

Ксперименте мы изучаем две величины х и у и проводим n измерений, получим набор из n-пар чисел(х1,у1),(х2,у2)…(x_n,y_n).

Предположим, что узависит от х и получим зависимость в виде формулы

график

Можем нанести тохки (х_і, у_і) на координатную плоскость и попитаться подобрать такую кривую у=ф(х), которая наилучшим образом приближала бы эти точки. Такая кривая назыв.эмпирической кривой, а ее уравнение у=ф(х) – эмпирической зависимостью.

Можно провести кривую в точности через точки (х, у). такая задача назыв.задачей интерполяции и решена для различных случав, но получ.формулы слишком сложные.

Суть метода:

1. для каждой точки х_і вычеслить отклонение ординаты (у) экспериментальной точки (х_і,у_і) от точки на предпологаемой прямой (x_i,f(x_i)): /\i=|f(x_i) –y_i|

2. подбераем кривую y=f(x) так, чтобы сумма квадратов этих отклонений была бы наименьшей /\=Σ(i=1) /\внизу і вверху z.

Зависимость у=ф(х) полученная по этому методу назыв.эмпирической зависимостью в смысле наименьших квадратов.

Предположим, что результаты измеений (х_і,у_і) оказались расположені вдоль некоторой прямой. Тога в єтом случае будем искать линейную эмпирическую зависимость y=kx+b.

В этом случае суть метода наименьших квадратов состоит в поиске коэфициенов к и в так, чтобв сумма квадратов отклонений была наименьшей: /\=Σ от i=1 до n(kx_i+b-y_i)2=F(k;b).

Для нахождение линейной эмпирической зависимости используют формулу для вычисления точки минимума F(k0,b0):

{kΣот і=1 до n xi^2+bΣ от і=1 до n - Σот і=1 до n yixi=0

{kΣот і=1 до n xi + nb - Σот і=1 до n y1 =0

Для численного нахождения искомых параметров k и b удобно составлять таблицу (і|xi|yi|xi^2|xiyi|.

36. ф-цию Ф(х) называют первообразной ф-ции ф(х) на промежутке(а,в), если для любого хє(а,в):F `(x)=f(x) dF(x)=f(x) dx

Все первообразные ф-ции ф(х) на промежутке (а,в) отличаются на константу, т.е. если F(x) – какая-нибудь первообразная ф-ции ф(х), то Ф(х)+с – общий вид первообращной.

37. совокупность первообразных Ф(х)+с для данной ф-ции ф(х) обозначают Sf(x)dx и называют неопределенным интегралом:

Основные свойства неопределенного интеграла:

38. Метод разложения. Примеры

Неопределенный интеграл от любой рациональной дроби на всяком промежутке, на котором знаменатель дроби не обращается в ноль, существует и выражается через элементарные функции, а именно он является алгебраической суммой суперпозиции рациональных дробей, арктангенсов и рациональных логарифмов.

Сам метод заключается в разложении рациональной дроби на сумму простейших дробей.

Всякую правильную рациональную дробь , знаменатель которой разложен на множители

можно представить (и притом единственным образом) в виде следующей суммы простейших дробей:

где  — некоторые действительные коэффициенты, обычно вычисляемые с помощью метода неопределённых коэффициентов.

Пример .

Представим подынтегральную функцию в виде суммы двух дробей и, используя свойство 50, запишем интеграл в виде суммы двух интегралов. Для каждого из полученных интегралов применим метод внесения под знак дифференциала.

39. Метод подстановки. Примеры

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

Пусть требуется вычислить интеграл . Сделаем подстановку , где  — функция, имеющая непрерывную производную.

Тогда и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:

Примеры .

1. Воспользуемся методом замены переменной. Введем новую переменную t по формуле . Тогда  или . Тогда

40. Определенный интеграл. Определение, физическая и геометрическая

Пусть f(x) определена на [a;b]. Разобьём [a;b]на части с несколькими произвольными точками a = x0 < x1 < x2 < xn = b Тогда говорят, что произведено разбиение RR отрезка [a;b] Далее выберем произв. точку , i = 0, Определённым интегралом от функции f(x) на отрезке [a;b]называется предел интегральных сумм ΘR при , если он существует независимо от разбиения R и выбора точек ξi, т.е. (1) Если существует (1), то функция f(x) называется интегрируемой на [a;b] – определение интеграла по Риману.

a – нижний предел.

b – верхний предел.

f(x) – подынтегральная функция.

λR - длина частичного отрезка.

σR – интегральная сумма от функции f(x) на [a;b] соответствующей разбиению R.

λR - максимальная длина част. отрезка.

Пусть на отрезке [а; b] задана непрерывная функция у = ƒ(х) ≥ 0. Фигура, ограниченная сверху графиком функции у = ƒ(х), снизу — осью Ох, сбоку — прямыми х = а и х = b, называется криволинейной трапецией. Найдем площадь этой трапеции.

Для этого отрезок [а; b] точками а=х0, х1, ..., b=хn (х0<x1<...<xn) paзобьем на n частичных отрезков [хо;х1], [х1;х2],...,[хn-1;хn]. (см. рис. 168). В каждом частичном отрезке [xi-1;xi] (i=1,2,..., n) возьмем произвольную точку ci и вычислим значение функции в ней, т. е. ƒ(ci).

Умножим значением функции ƒ(ci) на  длину ∆xi=xi-xi-1 соответствующего частичного отрезка. Произведение ƒ(ci) • ∆xi равно площади прямоугольника с основанием ∆xi и высотой ƒ(ci). Сумма всех таких произведений

равна площади ступенчатой фигуры и приближенно равна площади S криволинейной трапеции:

С уменьшением всех величин Δхi точность приближения криволинейной трапеции ступенчатой фигурой и точность полученной формулы увеличиваются. Поэтому за точное значение площади S криволинейной трапеции принимается предел S, к которому стремится площадь ступенчатой фигуры Sn, когда n неограниченно возрастает так, что λ = max∆xi →0:

Итак, определенный интеграл от неотрицательной функции численно равен площади криволинейной трапеции.

В этом состоит геометрический смысл определенного интеграла.

Пусть материальная точка М перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину F = F(x), где х — абсцисса движущейся точки М.

Найдем работу А силы F по перемещению точки М вдоль оси Ох из точки х = а в точку х = b (а < b). Для этого отрезок [а; b] точками а = х0, х1, ..., b = хn (х0 < x1 < ... < хn) разобьем на n частичных отрезков [х0; x1], [x1; x2],..., [xn-1; xn]. Сила, действующая на отрезке [xi-1; xi], меняется от точки к точке. Но если длина отрезка Δхi = хi-xi-1 достаточно мала, то сила F на этом отрезке изменяется незначительно. Ее можно приближенно считать постоянной и равной значению функции F = F(x) в произвольно выбранной точке х = ci Î [xi-1; xi]. Поэтому работа, совершенная этой силой на отрезке [xi-1;xi], равна произведению F(ci)•Δхi (Как работа постоянной силы F(ci) на участке [xi-1; xi].) Приближенное значение работы А силы F на всем отрезке [а; b] есть

Это приближенное равенство тем точнее, чем меньше длина Δхi Поэтому за точное значение работы А принимается предел суммы (36.1) при условии, что наибольшая длина λ частичных отрезков стремится к нулю:

В этом состоит физический смысл определенного интеграла.

41. Формула Ньютона-Лейбница Если функция f (x) интегрируема на [a; b], то для любого существует интеграл

который называется интегралом с переменным верхним пределом.

Если функция f интегрируема на [a; b], то функция F (x) непрерывна на этом отрезке.

Если функция f интегрируема на [a; b] и непрерывна в то функция F (x) дифференцируема в  причем

Если функция f непрерывна на [a; b], то на этом отрезке она имеет первообразную F вида

где C – постоянная. Всякая первообразная функции f на отрезке [a; b] удовлетворяет этой формуле.

 

Одним из основных результатов математического анализа является теорема Ньютона – Лейбница:

Пусть функция f (x) непрерывна на [a; b], а F (x) – какая-либо первообразная функции f на этом отрезке. Тогда

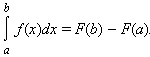
Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f, вычислить ее значения в точках a и b и найти разность F (b) – F (a).

Пусть f (x) непрерывна на [a; b], g (t) имеет непрерывную производную на [α; β], Тогда если a = g (α), b = g (β), то справедлива формула замены переменной в определенном интеграле:

Если функции u (x) и v (x) имеют на [a; b] непрерывные производные, то справедлива формула интегрирования по частям: