Уравнения локальной теплоотдачи Температура смешения

Плотность теплового потока от стенки к жидкости в сечении рассчитывается по формуле Ньютона

, (Т16)

где – температурный напор в сечении , – так называемая температура смешения, или иначе среднерасходная температура потока, которую будет иметь жидкость, если перемешивать движущийся поток жидкости.

Следует понимать, что эта температура не совпадает со средней интегральной по сечению температурой жидкости, так как в потоке центральные слои движутся быстрее и переносят большее количество жидкости, чем пристенные, и их вклад в среднюю температуру окажется больше (при равной площади сечения).

Если считать и , то температуру смешения можно рассчитать по формуле

, (Т17)

где V – объемный расход через сечение, , f – площадь сечения, а – элемент этой площади.

Напомним, что среднеинтегральная по сечению температура рассчитывалась бы по формуле . Формула (Т17) учитывает скорости перемещения жидкости.

В частности, за выходную температуру следует принимать температуру смешения в выходном сечении трубы.

Теплоотдача на участке стабилизированного теплообмена

Коэффициент теплоотдачи в (Т16) определяется, как обычно в конвективном теплообмене, по числу Нуссельта

.

Для стабилизированного теплообмена на ламинарном режиме при фиксированной температуре стенки известно теоретическое решение (а для случая будет ).

В практическое уравнение подобия добавляется поправка на неизотермичность

, (Т18)

определяющая температура – , используется для определения , а также в числе Нуссельта

. (Т19)

Теплоотдача на начальном участке

Как отмечалось выше, в случае ламинарного режима часто бывает важно учитывать влияние начального участка. Считается, что теплообмен будет заметно увеличен в его первой части, при (сравните с (Т14) ), то есть при

. (Т20)

Левая часть этого равенства и служит основой для поправочного множителя к (Т18), с которым получается формула

,

или в типичной для уравнения подобия форме

, (Т21)

Таким образом, уравнение (Т21) используется на участке (Т20), а при бóльших используется (Т18).

Необходимо иметь в виду, что эти формулы справедливы только на вязкостном режиме, при малом влиянии свободно-конвективного движения. О последнем будет говориться ниже.

Формулы для локальной теплоотдачи на турбулентном и переходном режимах здесь не рассматриваются – их можно найти в справочниках.

Уравнения для расчета общей теплоотдачи

Хотя теоретически общий тепловой поток может быть найден по формуле (Т2) через локальную плотность теплового потока (Т16), для практических расчетов нужна формула более простого и удобного вида

, (Т22)

где – среднее по поверхности трубы значение коэффициента теплоотдачи, – средний температурный напор. Значение определяется по числу , которое в свою очередь определяется по соответствующему уравнению подобия, об этом будет говориться ниже. Сейчас рассмотрим вопрос о расчете .

Понятие среднелогарифмического температурного напора

а) Распределение температуры при .

В этом случае . Построим распределение .

Перейдем к избыточной температуре , тогда при будет . Кроме того, обозначим . Рассмотрим элемент трубы длиной с координатой сечения (рис. …).

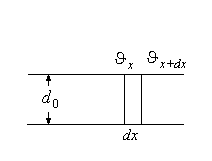
Приращение внутренней энергии жидкости при прохождении этого элемента

(Т23)

по условию баланса теплоты должно быть равно количеству теплоты, переданному жидкости от стенок

. (Т24)

Учитывая , , , (площадь поверхности трубы в элементе), и приравнивая (Т23) и (Т24), получаем уравнение относительно :

или

.

Обозначая , получаем для уравнение вида , интегрирование которого даёт , или

(Т25)

То есть распределение избыточной температуры описывается экспонентой

, (Т26)

где

. (Т27)

Последнее равенство следует из постановки при в (Т25).

б) Средний температурный напор.

По определению , и при распределении (Т26) будет . Учитывая, что по (Т26) и по (Т27), получаем .

Переходя от термина и обозначения избыточной температуры к понятию температурного напора, и учитывая, что , , получаем, что при распределении (Т26), имеющем место в случае , , среднеинтегральный температурный напор равен

(Т28)

При этом общий тепловой поток трубы подсчитывается по формуле (П2)

.

Рассчитанное по (Т28) значение называется среднелогарифмическим температурным напором, в отличие, например, от среднеарифметического

. (Т29)

Формула (Т28) – это формула осреднения экспоненциальной функции.

Чтобы лучше показать смысл введения среднелогарифмического температурного напора (Т28), построим графики температур, соответ­ству­ющих распределению (Т26) (рис. …). Видно, что график 1 температуры и, соответственно, распределение напора (расстояние от сплошной кривой до уровня ) может сильно отличаться от линейной зависимости (штриховая прямая 2). Вследствие этого и среднеинтегральное значение будет существенно отличаться от среднеарифметического (среднеинтегрального для прямой)

В реальных процессах значения меняются по длине трубы, но характер изменения температурного напора близок к изображенному на рис. … экспоненциальному, поэтому для расчета в (Т22) также следует применять формулу (Т28) для среднелогарифмического напора. Впрочем, полезно иметь в виду, что при небольших изменениях отличие графика от линейного будет небольшим, и . Так, при отличие от составит менее 4%, а при – менее 3% . Поэтому в таких случаях вместо по (Т28) можно использовать более простую формулу (Т29) для .