Теплообмен при вынужденном течении жидкости в трубах Общие определения

Будем считать, что рассматривается течение несжимаемой жидкости внутри круглой гладкой прямой трубы постоянного сечения, процесс теплообмена установившийся. Это один из важнейших случаев теплообмена в инженерной практике. Пусть внутренний диаметр трубы (такое обозначение позволяет отличать его от математического символа дифференциала, вроде ), длина (рис. …). Скорость жидкости на входе постоянна по сечению и равна (то есть поток на входе равномерный, например, благодаря гладкому входу из большой емкости), а температура – . Температура стенок трубы постоянна и равна . Теплофизические характеристики жидкости известны. Типичная задача: при заданных и установить связь , , со средней выходной температурой жидкости , с общим тепловым потоком (передаваемым от трубы к жидкости) , с распределением плотности теплового потока , Вт/м², по длине трубы, со средней плотностью теплового потока и с другими параметрами.

Ясно, что искомые параметры связаны между собой балансовыми соотношениями. Например, с учетом того, что массовый расход жидкости равен , кг.с ( – площадь поперечного сечения трубы), имеет место связь и :

, Вт. (Т1)

По определению

, (Т2)

где – площадь внутренней поверхности трубы.

При этом, как отмечалось выше, величина связана со средней температурой жидкости в сечении формулой Ньютона

(Т3)

где – коэффициент теплоотдачи в сечении трубы.

Таким образом, проблема расчета параметров теплообмена в трубе сводится к определению значений (и/или среднего значения ). Кроме того, важной характеристикой являются потери давления (разность давлений на входе и на выходе), связанные с мощностью, затрачиваемой на прокачку жидкости через трубу:

, Вт. (Т4)

Напомним, что несжимаемой жидкостью можно считать не только капельную жидкость, но и газ при умеренных скоростях (до 1/3 скорости звука).

Гидродинамика течения в трубе Основные сведения

Вспомним материал о течении жидкости в круглой трубе из курса Гидрогазодинамики.

Режим в трубе может быть ламинарным, переходным или турбулентным, что определяется числом Рейнольдса

. (Т5)

При режим ламинарный, при – переходный, при – турбулентный. Значения критических чисел Рейнольдса обычно можно считать равными

(иногда принимают ), .

(Т6)

Отличие значений от случая пластины объясняется выбором в качестве определяющего размера диаметра , а не длины . Следует иметь в виду, что реально режим определяется поперечным размером потока, поперёк которого происходит изменение скорости от 0 до , и в должны развиваться вихри. То есть выбор поперечного размера трубы в качестве определяющего логичен. А в случае пластины нет заданного поперечного размера, толщина пограничного слоя, собственно и определяющая режим, неизвестна. Но она связана с продольной длиной или расстоянием от начала пластины . Поэтому в случае пластины приходиться использовать продольный размер. Если ввести число Рейнольдса с пересчетом по (или ), то критические числа для пластины будут иметь тот же порядок, что и для трубы.

Если, поток на входе равномерный, как было указано выше, то у стенок, начиная со входа, формируется пограничный слой, подобно погранслою на пластине. Но имеются и особенности (рис. …).

а) Так как расход жидкости через любое сечение один тот же, то из-за торможения в погранслое у стенок скорость жидкости в центральной части растёт, происходит как бы вытеснение движущейся жидкости от стенок в центральную часть.

б) Если , то толщина ламинарного погранслоя растет, пока не достигнет величины радиуса трубы , когда погранслой смыкается на оси и захватывает всё сечение трубы. Участок длиной от начала трубы до места смыкания называется гидродинами­ческим начальным участком. Далее идет участок стабилизированного течения. На нем, если характеристики жидкости не меняются, профиль скорости одинаков во всех поперечных сечениях.

В ламинарном изотермическом режиме такой профиль в соответствии с теоретическим решением является параболой

, (Т7)

где – радиус трубы, – расстояние от оси трубы, .

Считая, что средняя скорость в произвольном поперечном сечении трубы – это отношение объёмного расхода через сечение к его площади : то есть , получаем ввиду постоянстве расхода (по условию баланса массы или объема), что . С другой стороны, подсчитывая расход через сечение на участке стабилизированного течения по известному распределению скорости (Т7), имеем, что расход жидкости dV через “элементарное” кольцо радиуса r и ширины dr равен (где - площадь кольца), то есть по (Т7) 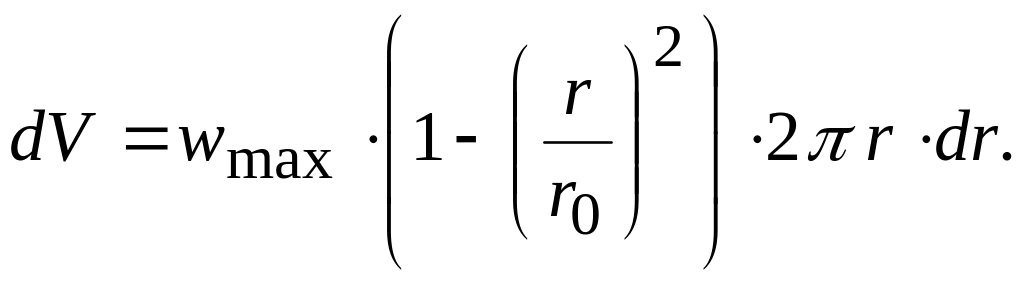Тогда расход через все сечение равен

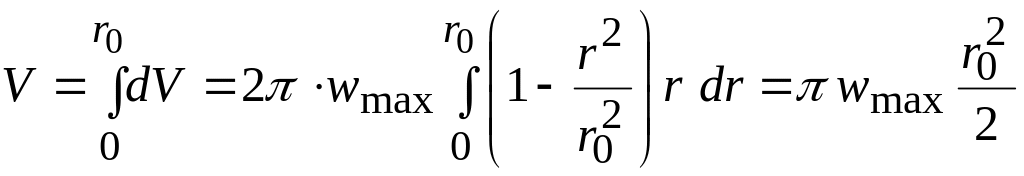, и .

Таким образом, на таком режиме максимальная скорость в середине трубы равно в два раза больше средней (или входной) скорости :

. (Т8_лам)

Длина гидродинамического начального участка на ламинарном режиме оказывается довольно большой и определяется формулой

. (Т9)

При пограничный слой, начинающийся как ламинарный, переходит в турбулентный и лишь затем смыкается. При турбулентном режиме у стенок существует тонкий вязкий подслой с ламинарным режимом (рис. …).

При очень больших числах Рейнольдса пограничный слой практически сразу становится турбулентным. При этом длина гидродинамического начального участка составляет величину порядка

. (Т10)

В турбулентном потоке на участке стабилизированного течения профиль скорости из-за сильного перемешивания слабо переменный в центральной (турбулентной) части, а основное изменение скорости имеет место в вязком подслое (рис. …).

Поэтому здесь

(Т8_турб)

( – осредненная по времени скорость на оси трубы).