
Системный анализ / 21. Задача комммивояжера (МВГ)
.DOC
Решение задачи о коммивояжере методом ветвей и границ
Было бы, конечно, несправедливо по отношению к такому мощному методу, каким является метод ветвей и границ, ограничиться рассмотрением только метода Лэнд и Дойг и не затронуть вообще комбинаторные задачи. Тем более, как уже было отмечено, впервые термин "ветви и границы" прозвучал при решении комбинаторной задачи - зазачи о коммивояжере (1963г.).
Сейчас мы попробуем "разработать" алгоритм решения этой задачи с использованием метода ветвей и границ.
Пусть A1, A2,..., An, - множество городов.
C=(cij) - квадратная матрица "расстояний" между городами прядка n.
Пусть коммивояжер выезжает из города A1 и возвращается в этот город, побывав в каждом из остальных городов по одному разу.
Пусть, далее, -
множество всех возможных маршрутов.
Обозначим ![]() (2 k n-1)
подмножество всех допустимых маршрутов,
каждый из которых характеризуется
тем, что выезжая из города A1,
коммивояжер последовательно посещает
города
(2 k n-1)
подмножество всех допустимых маршрутов,
каждый из которых характеризуется
тем, что выезжая из города A1,
коммивояжер последовательно посещает
города
![]() ,
а затем - оставшиеся города и возвращается
в город A1.
,
а затем - оставшиеся города и возвращается
в город A1.
Конкретизируем принцип ветвления.
Пусть коммивояжер находится в пункте A1 - в исходном пункте. Выбором первого города, в который нужно въехать из A1, множество всех возможных маршрутов разбивается на непересекающиеся подмножества 1,2, 1,3,... 1,n:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1,2 |
|
1,3 |
......... |
1,n |
|||||
Пусть теперь после посещения городов
![]() (2 k n-1)
принимается решение о выборе очередного
города в который нужно въехать, выехав
из города
(2 k n-1)
принимается решение о выборе очередного
города в который нужно въехать, выехав
из города
![]() .
.
Фактически, этим решением множество
допустимых маршрутов
![]() разбивается
на подмножества:
разбивается
на подмножества:
![]() где j{1,i2,i3,...,in}.
где j{1,i2,i3,...,in}.
Очевидно, что подмножество
![]() состоит из одного - единственного
маршрута:
состоит из одного - единственного
маршрута:

![]()
 ,
где in{1,i2,i3,...,in-1}.
,
где in{1,i2,i3,...,in-1}.
Выбора нет!
Итак, мы конкретизировали принцип ветвления.
Конкретизируем принцип вычисления нижней границы (оценки)
Здесь "возможны варианты". Рассмотрим один из них.
Оценку подмножества
![]() (2 k n-1)
будем вычислять следующим образом:
(2 k n-1)
будем вычислять следующим образом:
(![]() )=
)=
![]() +
+![]() +...+
+...+![]() +
+
+ +(n-k)
+(n-k)
 .
.
Здесь:
![]() +
+![]() +...+
+...+![]() -
фактическая стоимость всех, уже
"состоявшихся" переездов;
-
фактическая стоимость всех, уже
"состоявшихся" переездов;
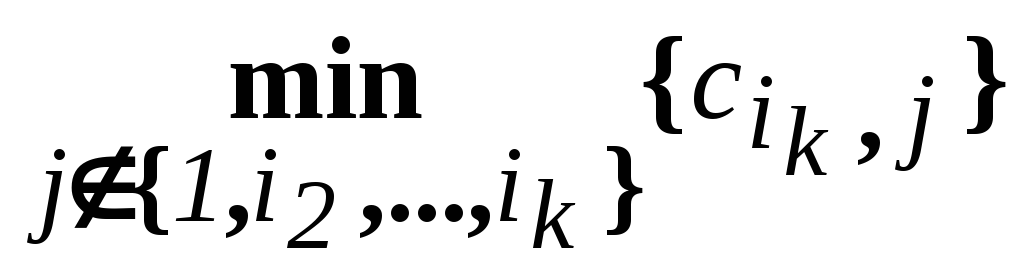 -
стоимость самого короткого переезда
из пункта ik
в пункт j , в котором
еще не был коммивояжер;
-
стоимость самого короткого переезда
из пункта ik
в пункт j , в котором
еще не был коммивояжер;
(n-k) - количество оставшихся переездов;

 -
стоимость самого короткого из оставшихся
переездов.
-
стоимость самого короткого из оставшихся
переездов.
Очевидно, что при k=n-1
оценка (![]() )
совпадает со стоимостью единственного
маршрута, составляющего множество
)
совпадает со стоимостью единственного
маршрута, составляющего множество
![]() - это стоимость маршрута:
- это стоимость маршрута:
![]() ,
где in{1,i2,i3,...,in-1}.
,
где in{1,i2,i3,...,in-1}.
Как видно, предложенная оценка весьма "оптимистическая". Однако, по мере продвижения (по мере разбиения множества допустимых маршрутов) эта оценка уточняется - убывать, в принципе, не может.
Таким образом, конкретизирован еще один принцип метода ветвей и границ - принцип уточнения оценок.
Теперь о последнем принципе - о принципе оптимальности.
Здесь вполне естественна следующая схема.
Имеется список подмножеств допустимых маршрутов.
Каждое из этих подмножеств имеет свою оценку.
Пусть на очередном шаге работы алгоритма из списка выбирается подмножество с минимальной оценкой.
Если этому подмножеству соответствует полный маршрут (т.е. k=n-1) , то этот маршрут является оптимальным.
Пример
В задаче нужно объехать 5 городов, выехав из города1. Стоимости переездов представлены в таблице.
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
4 |
9 |
6 |
1 |
|
2 |
2 |
|
9 |
2 |
10 |
|
3 |
11 |
11 |
|
8 |
1 |
|
4 |
5 |
4 |
3 |
|
8 |
|
5 |
1 |
11 |
1 |
8 |
|
Шаг 1. Разбиваем полное множество всех маршрутов на 4 подмножества:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
13 |
|
14 |
|
15 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Находим оценку (нижнюю границу) каждого из этих подмножеств.
Подмножество 12:
![]()
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
4 |
9 |
6 |
1 |
|
2 |
2 |
|
9 |
2 |
10 |
|
3 |
11 |
11 |
|
8 |
1 |
|
4 |
5 |
4 |
3 |
|
8 |
|
5 |
1 |
11 |
1 |
8 |
|
(12)=c12+![]() +(5-2)
+(5-2)
 =4+2+31=9
=4+2+31=9
Подмножество 13:
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
4 |
9 |
6 |
1 |
|
2 |
2 |
|
9 |
2 |
10 |
|
3 |
11 |
11 |
|
8 |
1 |
|
4 |
5 |
4 |
3 |
|
8 |
|
5 |
1 |
11 |
1 |
8 |
|
(13)=c13+![]() +(5-2)
+(5-2)
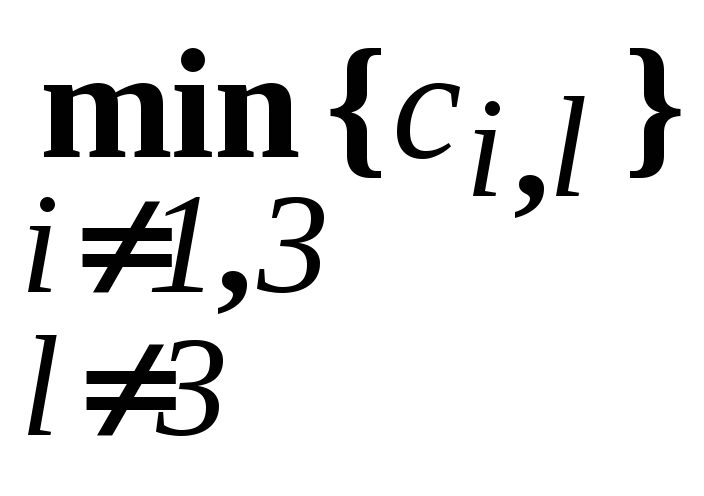 =9+1+31=13
=9+1+31=13
Подмножество 14:
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
4 |
9 |
6 |
1 |
|
2 |
2 |
|
9 |
2 |
10 |
|
3 |
11 |
11 |
|
8 |
1 |
|
4 |
5 |
4 |
3 |
|
8 |
|
5 |
1 |
11 |
1 |
8 |
|
(14)=c14+![]() +(5-2)
+(5-2)
 =6+3+31=12
=6+3+31=12
Подмножество 15:
|
|
1 |
2 |
3 |
4 |
5 |
|
1 |
|
4 |
9 |
6 |
1 |
|
2 |
2 |
|
9 |
2 |
10 |
|
3 |
11 |
11 |
|
8 |
1 |
|
4 |
5 |
4 |
3 |
|
8 |
|
5 |
1 |
11 |
1 |
8 |
|
(15)=c15+![]() +(5-2)
+(5-2)
 =1+1+32=8
=1+1+32=8
Заносим подмножества (вместе с оценками) в список.
Из списка выбирается подмножество с минимальной оценкой (это 15 с оценкой 8).
Подмножество 15 разбивается на 3 подмножества:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
13 |
|
|
12 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
13 |
|
14 |
|
15 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
152 |
|
153 |
|
154 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вычисляются нижние границы вновь образованных подмножеств.
Подмножество 152 :
(152)=c15+
c52+![]() +(5-3)
+(5-3)
 =1+11+2+23=20
=1+11+2+23=20
Подмножество 153 :
(153)=c15+
c53+![]() +(5-3)
+(5-3)
 =1+1+8+22=14
=1+1+8+22=14
Подмножество 154 :
(154)=c15+
c54+![]() +(5-3)
+(5-3)
 =1+8+3+22=16
=1+8+3+22=16
Заносим подмножества (вместе с оценками) в список.
Из списка выбирается подмножество с минимальной оценкой (это 12 с оценкой 9).
Подмножество 15 разбивается на 3 подмножества:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
13 |
|
|
12 |
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
12 |
|
13 |
|
14 |
|
15 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
14 |
|
|
16 |
|
123 |
|
124 |
|
125 |
|
|
|
|
|
152 |
|
153 |
|
154 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
