
- •Транспортная задача
- •Построение сбалансированной транспортной модели
- •Сведение многопродуктовой модели транспортной задачи к однопродуктовой
- •Свойства закрытой транспортной задачи
- •1. Задача в любом случае допустима и имеет решение.
- •Построение исходного опорного решения транспортной задачи
- •Метод северо-западного угла
- •Метод наименьшей стоимости
- •Алгоритм
- •Приближенный метод Фогеля
- •Алгоритм
- •Метод плавающих зон
- •Метод потенциалов
- •Использование второй теоремы двойственности для обоснования метода потенциалов
- •Метод потенциалов. Переход к новому опорному решению
- •Выводы по методу потенциалов
- •Теорема о цикле пересчета
- •Распределительный метод решения транспортной задачи
- •Алгоритм распределительного метода
- •Дополнительные ограничения в постановке транспортной задачи
- •Контроль
- •Транспортная модель с промежуточными пунктами
Распределительный метод решения транспортной задачи
Наиболее трудоемким этапом в методе потенциалов является этап построения цикла пересчета для переменной, которая имеет отрицательную косвенную стоимость.
Если бы не трудоемкость этого этапа, можно было бы поступить по-другому: сначала для свободной переменной построить цикл пересчета, а после этого принять решение, следует ли эту переменную вводить в состав базисных переменных нового опорного решения или нет. То есть, вообще отказаться от вычисления потенциалов.
На этом построен распределительный метод решения транспортной задачи.
Пусть имеется
некоторое опорное решение и
![]() - свободная переменная, а
- свободная переменная, а![]() - базисная
переменная.
- базисная
переменная.
Построим цикл
пересчета для
![]() .
.
Что касается
![]() ,
возможны следующие ситуации.
,
возможны следующие ситуации.
 соответствует
положительной вершине;
соответствует
положительной вершине; соответствует
отрицательной вершине;
соответствует
отрицательной вершине; в цикл не входит.
в цикл не входит.
Если
 соответствуетположительной вершине,
то при переходе к новому опорному
решению
соответствуетположительной вершине,
то при переходе к новому опорному
решению увеличитсяна ту же величину,
что и
увеличитсяна ту же величину,
что и .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная войдет в выражение для
войдет в выражение для с коэффициентом «+1»;
с коэффициентом «+1»;Если
 соответствуетотрицательной вершине,
то при переходе к новому опорному
решению
соответствуетотрицательной вершине,
то при переходе к новому опорному
решению уменьшитсяна ту же величину,
на которую увеличится
уменьшитсяна ту же величину,
на которую увеличится .
То есть, если выразить базисные переменные
через свободные, переменная
.
То есть, если выразить базисные переменные
через свободные, переменная войдет в выражение для
войдет в выражение для с коэффициентом "-1";
с коэффициентом "-1";Если
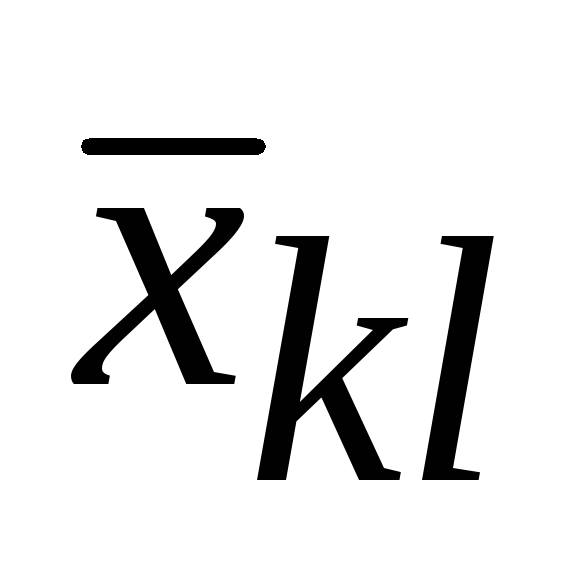 не входит в цикл пересчета, то
при переходе к новому опорному решению
значение
не входит в цикл пересчета, то
при переходе к новому опорному решению
значение не изменится. То есть, если выразить
базисные переменные через свободные,
переменная
не изменится. То есть, если выразить
базисные переменные через свободные,
переменная войдет в выражение для
войдет в выражение для с коэффициентом "0".
с коэффициентом "0".
Схематично эти ситуации можно представить следующим образом:
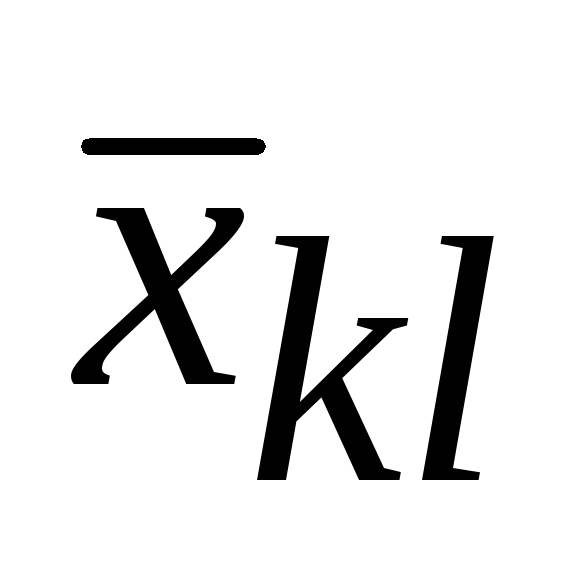 = +1
= +1 +…….
+……. = -1
= -1 +…….
+……. = 0
= 0 +…….
+…….
Выразим теперь ЦФ через свободные переменные.
Как подсчитать, с
каким коэффициентом переменная
![]() войдет
в ЦФ?
войдет
в ЦФ?
Она войдет в
соответствующее выражение непосредственно
(с коэффициентом
![]() )
и через посредство тех и только тех
базисных переменных, которые входят в
цикл пересчета.
)
и через посредство тех и только тех
базисных переменных, которые входят в
цикл пересчета.
Но
![]() входит в выражение для
входит в выражение для![]() только с одним из двух коэффициентов:
+1 или -1 , в зависимости
от того, является ли вершина
только с одним из двух коэффициентов:
+1 или -1 , в зависимости
от того, является ли вершина![]() положительной
или отрицательной. А
положительной
или отрицательной. А![]() входит
в ЦФ с коэффициентом
входит
в ЦФ с коэффициентом![]() .
То есть, посредством
.
То есть, посредством![]() (входящей в цикл) переменная
(входящей в цикл) переменная![]() войдет в ЦФ с коэффициентом
+
войдет в ЦФ с коэффициентом
+![]() или -
или -![]() в
зависимости от того, является ли вершина
в
зависимости от того, является ли вершина![]() положительной
или отрицательной.
положительной
или отрицательной.
Схематично эту ситуацию можно представить следующим образом:
Z=![]()
![]() +
+![]()
![]() +…
+…

![]() =
= +…
+…
Z=![]()
![]() +
+![]() (
( +…)+…
+…)+…
Z=
![]() +…
+…
Как видно из этого выражения, в круглых скобках записана алгебраическая сумма всех стоимостей, которым соответствуют вершинам цикла пересчета.
Таким образом,
коэффициент, с которым свободная
переменная
![]() входит в ЦФ, равен алгебраической сумме
всех стоимостей, соответствующих
вершинам цикла, включая вершину, в
которой находится свободная переменная.
входит в ЦФ, равен алгебраической сумме
всех стоимостей, соответствующих
вершинам цикла, включая вершину, в
которой находится свободная переменная.
То есть, косвенную
стоимость свободной переменной
![]() можно определить не по формуле
можно определить не по формуле![]() ,
а другим путем. Нужно построить для этой
переменной цикл пересчета и подсчитать
алгебраическую сумму всех стоимостей,
которым соответствуют вершинам цикла
пересчета.
,
а другим путем. Нужно построить для этой
переменной цикл пересчета и подсчитать
алгебраическую сумму всех стоимостей,
которым соответствуют вершинам цикла
пересчета.
Алгоритм распределительного метода
Имеется некоторое опорное решение.
Шаг 1. Для данного опорного решения организуем последовательный просмотр списка свободных клеток (переменных).
Шаг 2. Для
очередной свободной клетки (пусть это
будет![]() ),
строим цикл пересчета и подсчитываем
алгебраическую сумму стоимостей по
всем вершинам цикла (
),
строим цикл пересчета и подсчитываем
алгебраическую сумму стоимостей по
всем вершинам цикла (![]() ).
).
Шаг 3. Если![]() < 0,
выполняемшаг 4. В противном
случае проверяем, все ли свободные
клетки просмотрены. Если да, то очередное
решениеоптимальное.Конец.
В противном случае выполняемшаг 2.
< 0,
выполняемшаг 4. В противном
случае проверяем, все ли свободные
клетки просмотрены. Если да, то очередное
решениеоптимальное.Конец.
В противном случае выполняемшаг 2.
Шаг 4. Переменную![]() вводим в состав базисных переменных.
Для этого среди отрицательных вершин
находим вершину с минимальным значением
соответствующей базисной переменной.
Пусть это будет
вводим в состав базисных переменных.
Для этого среди отрицательных вершин
находим вершину с минимальным значением
соответствующей базисной переменной.
Пусть это будет![]() .
Производим сдвиг по циклу пересчета.
Переменная
.
Производим сдвиг по циклу пересчета.
Переменная![]() выводится из состава базисных переменных.
Имеем новое опорное решение. Выполняемшаг 1.
выводится из состава базисных переменных.
Имеем новое опорное решение. Выполняемшаг 1.
Основной недостаток метода – большое количество циклов пересчета, которые приходится строить на каждой итерации. Достоинство – не нужно специально вычислять потенциалы строк и столбцов.
Если нет эффективной процедуры построения цикла пересчета, предпочтение отдается методу потенциалов.
Пример. Дана транспортная задача и известно ее опорное решение. Определить косвенные стоимости переменных x32,x34, x46.
|
|
15
5 |
20
|
25
|
15
|
10
|
10 10 |
20
|
|
|
5 20 |
5
|
1 30 |
4
|
2 50 |
1
|
15
|
|
E32=0 |
3
|
5
|
5
|
1
|
4
|
5 40 |
2
|
|
|
20
|
7 100 |
5
|
1 20 |
3
|
5
|
4
|
|
|
20
|
1 40 |
2 30 |
3
|
4
|
6
|
6 100 |
|
|
15
5 |
20
|
25
|
15
|
10
|
10 10 |
20
|
|
|
5 20 |
5
|
1 30 |
4
|
2 50 |
1
|
15
|
|
E34=2 |
3
|
5
|
5
|
1
|
4
|
5 40 |
2
|
|
|
20
|
7 100 |
5
|
1 20
|
3
|
5
|
4
|
|
|
20
|
1 40 |
2 30 |
3
|
4
|
6
|
6 100 |
|
|
15
5 |
20
|
25
|
15
|
10
|
10 10 |
20
|
|
|
5 20 |
5
|
1 30 |
4
|
2 50 |
1
|
15
|
|
E46=-2 |
3
|
5
|
5
|
1
|
4
|
5 40 |
2
|
|
|
20
|
7 100 |
5
|
1 20
|
3
|
5
|
4
|
|
|
20
|
1 40 |
2 30 |
3
|
4
|
6
|
6 100 |

 0
0 0
0 0
0