2.4. Внутренние усилия при изгибе

Под изгибом понимается такой вид нагружения стержня (балки), когда в его поперечных сечениях возникают только изгибающие моменты M_y (M_z) и перерезывающие (поперечные) силы Q_y (Q_z). Плоский поперечный изгиб вызывает внешняя нагрузка, перпендикулярная продольной оси балки. С геометрической точки зрения изгиб проявляется в искривлении ранее прямолинейной оси или изменении кривизны кривого стержня.

Перерезывающая сила считается положительной, если она направлена так, что стремится повернуть элемент балки по ходу часовой стрелки.

Изгибающий момент считается положительным, если он изгибает элемент балки выпуклостью вниз, вызывая растяжение нижних волокон.

Между изгибающим моментом, перерезывающей силой и распределенной нагрузкой существуют дифференциальные зависимости, которые позволяют весьма эффективно контролировать правильность построения эпюр внутренних силовых факторов.

Рассмотрим двухопорную балку, нагруженную внешней распределенной нагрузкой , направленной вверх (рис. 2.7). Выделим на расстоянии х бесконечно малый элемент dx. В связи с малостью элемента dx распределенную нагрузку на его длине можно считать постоянной ( ). В общем случае каждый из внутренних силовых факторов приобретает бесконечно малое приращение на длине dx. Уравнения равновесия для элемента dx запишутся

; (2.2)

; , (2 .3)

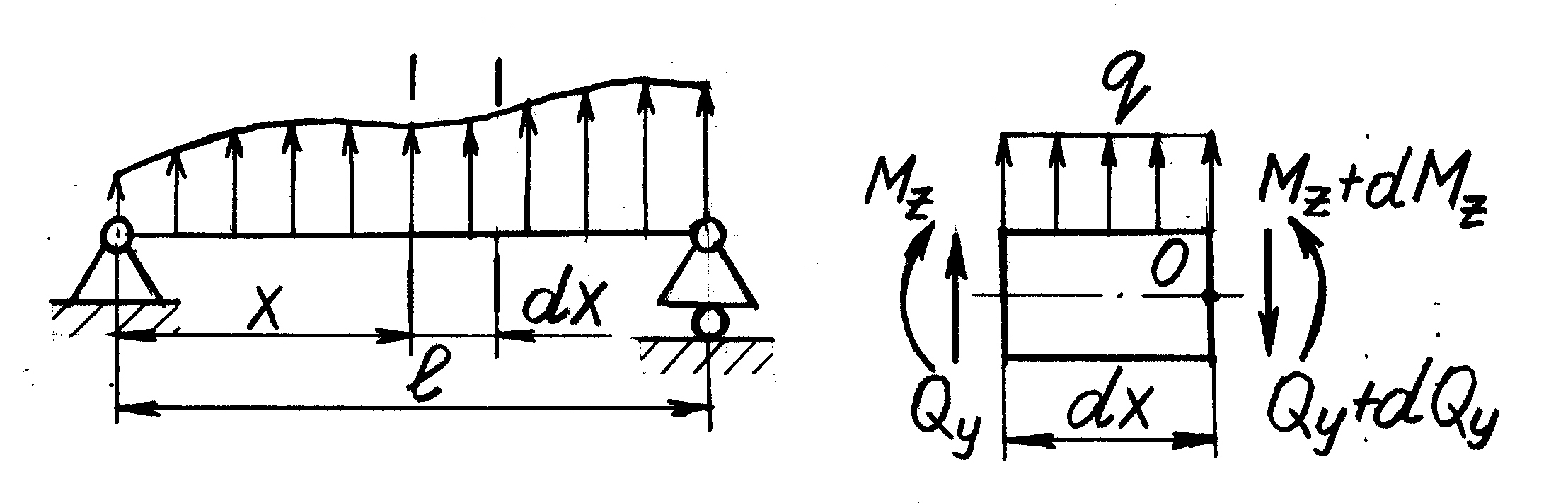
Рис. 2.7

так как , как величина второго порядка малости.

Зависимость (2.3) с учетом (2.2) может быть записана в виде

. (2.4)

Правила контроля правильности построения эпюр опираются на известные математике зависимости:

- производная численно равна тангенсу угла наклона между осью и касательной к графику функции ;

- производная пропорциональна в первом приближении кривизне кривой .

В качестве примера определения внутренних силовых факторов и построения их эпюр, рассмотрим консольную балку, нагруженную, как показано на рис. 2.8.

Исходные данные:

Сосредоточенная сила кН, распределенная нагрузка кН/м, внешний изгибающий момент кНм, длины участков м, м.

Определяем опорные реакции, для чего составляем уравнения равновесия статики:

,

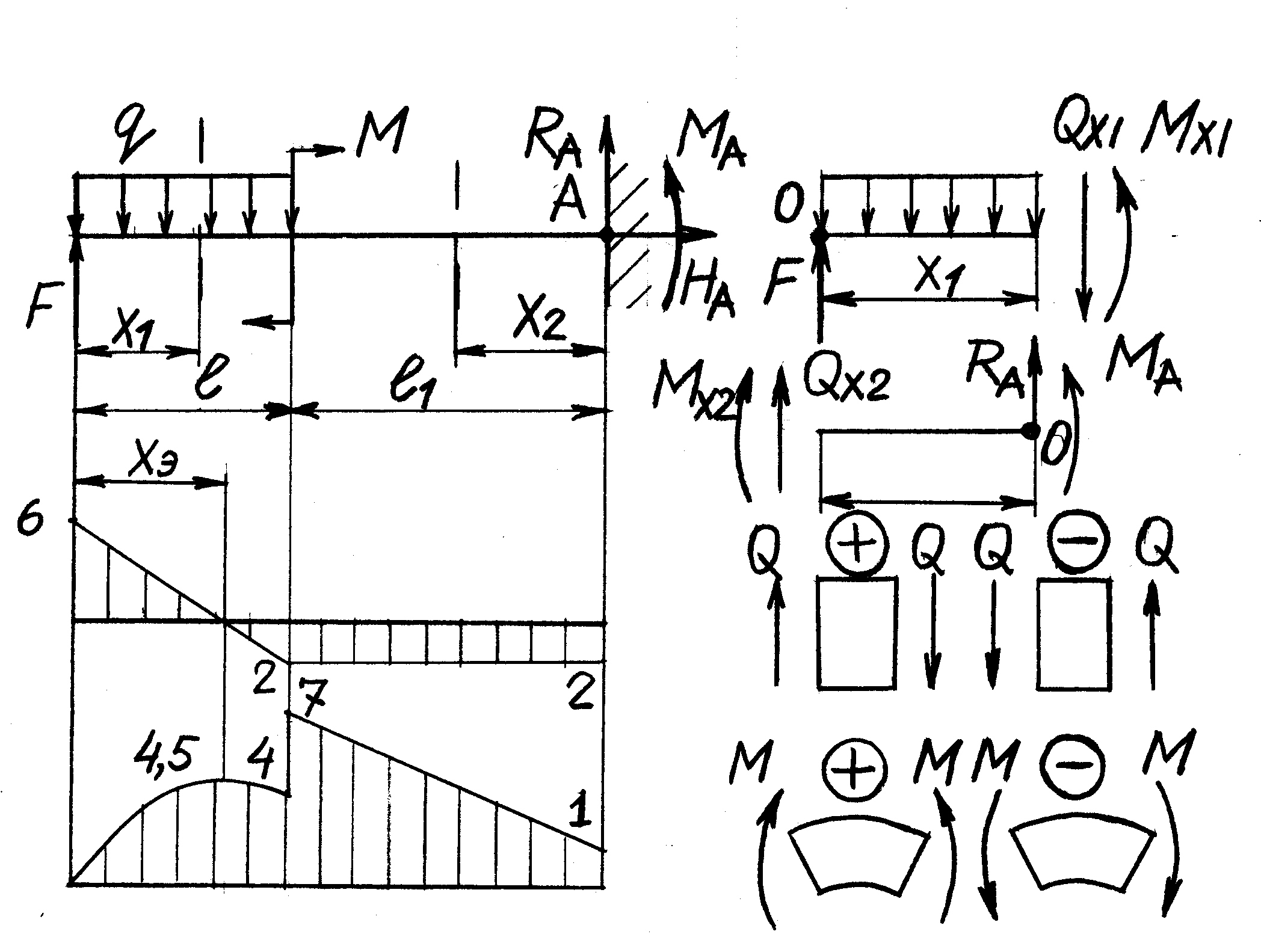
Рис. 2.8

В пределах левого участка на некотором расстоянии от левого конца проведем сечение. Уравнение равновесия левой отсеченной части стержня (при ) записывается следующим образом:

,

,

что позволяет получить выражения для расчета перерезывающей силы и изгибающего момента:

,

Уравнение для перерезывающей силы является уравнением прямой линии, так как в него входит в первой степени и для построения эпюры достаточно вычислить величины перерезывающих сил в двух точках: при кН и кН.

Уравнение для изгибающего момента - уравнение квадратной параболы. При q < 0 имеем < 0. Следовательно, эпюра изгибающего момента на участке 1 представляет собой кривую выпуклостью, направленной вверх. При , при кНм.

Поскольку на участке 1 перерезывающая сила переходит через нуль, меняя знак, то эпюра имеет экстремум. Для его вычисления необходимо определить координату сечения, в котором . Решая это уравнение относительно , найдем

м.

подставив это значение в уравнение момента, получим

кНм.

Для построения эпюр внутренних силовых факторов на правом участке балки, рассечем ее на некотором расстоянии от правого конца балки и рассмотрим равновесие правой отсеченной части:

,

;

При отсутствии на участке распределенной нагрузки перерезывающая сила const и, следовательно, эпюра изображается отрезком прямой, параллельной продольной оси балки.

Уравнение - уравнение прямой линии, при кН·м, при .

В инженерной практике обычно уравнения равновесия отсеченной части не рассматривают, а сразу записывают выражения для внутренних силовых факторов, пользуясь правилом знаков для перерезывающей силы и изгибающего момента. Согласно правилу, перерезывающая (поперечная) сила Q_y (Q_z ) в сечении равна алгебраической сумме проекций на ось у (z) всех внешних сил, приложенных по одну сторону (любую) от сечения, а изгибающий момент M_y (M_z) в данном сечении равен алгебраической сумме моментов относительно центра тяжести сечения от всех внешних сил, приложенных по одну сторону от данного сечения. При этом в левой отсеченной части балки внешние силы, направленные вверх, при определении перерезывающей силы в сечении складываются со знаком плюс; направленные вниз – со знаком минус. В правой отсеченной части балки соответственно наоборот. Как в левой, так и в правой отсеченной части балки, при определении изгибающего момента в сечении, внешние силы и моменты берутся со знаком плюс, если они стремятся повернуть вверх противоположный от сечения конец балки.

Правила контроля правильности построения эпюр:

1. На участке, где нет распределенной нагрузки ( ), перерезывающая сила постоянная, поэтому эпюра изображается отрезком прямой, параллельной продольной оси, а изгибающий момент отрезком прямой, наклонной к оси. Тангенс угла наклона эпюры равен силе . В частном случае, когда и , изгибающий момент постоянен.

2. На участке, где имеется равномерно распределенная нагрузка, эпюра изображается отрезком прямой, наклонной к продольной оси (тангенс угла наклона равен ), а эпюра изгибающего момента – квадратной параболой, у которой выпуклость направлена в сторону действия распределенной нагрузки.

Если на этом участке перерезывающая сила в одном из сечений равна нулю, то изгибающий момент в этом сечении принимает экстремальное значение. При построении эпюры слева направо, если меняет знак с плюса на минус, то изгибающий момент принимает максимальное значение, если меняет знак с минуса на плюс, то – минимальное значение.

3. В сечении, где приложена сосредоточенная сила , на эпюре будет скачок, равный значению этой силы и направленный в ту же сторону, а эпюра будет иметь перелом, направленный в сторону действия силы .

4. В сечении, где приложен сосредоточенный изгибающий момент на эпюре , будет скачок, равный значению момента. При этом направление скачка будет вверх (при построении эпюры слева направо), если сосредоточенный момент действует по ходу часовой стрелки, и вниз, если против хода часовой стрелки.

5. Если на некотором участке < 0, то эпюра на этом участке убывает, если > 0, то эпюра - возрастает.

Вопросы для самопроверки

1. Сформулируйте сущность метода сечений.

2. Перечислите внутренние силовые факторы.

3. Перечислите простые виды сопротивления стержня.

4. Правило знаков для внутренних силовых факторов при растяжении – сжатии, кручении и изгибе.

5. Какие дифференциальные соотношения между внутренними силовыми факторами имеют место при изгибе?

6. Перечислите правила контроля правильности построения эпюр внутренних силовых факторов.