1.4. Основные гипотезы

Как и всякая наука, сопротивление материалов базируется на ряде гипотез или до­пущений. Основные гипотезы, принятые в сопротивлении материалов, следующие.

1. Материал конструкции является сплошным (т. е. непрерывным), однородным и изотропным.

Сплошность или непрерывность означает, что материал занимает весь объём конструкции без пустот. Достоинство гипотезы сплошности материала состоит в том, что в сплошной среде деформации и перемещения точек являются непрерывными функциями координат, что позволяет применять методы математического анализа, та­кие как дифференциальное и интегральное исчисление.

Однородность материала подразумевает, что свойства его во всех точках одина­ковы, а изотропность – что материал обладает одинаковыми свойствами по всем на­правлениям. Реальный материал, например древесина, обладает различными механи­ческими свойствами вдоль волокон и поперек волокон.

2. Гипотеза о малости деформаций. Абсолютные деформации настолько малы по сравнению с размерами тела, что можно не учитывать их влияния на расстояния от на­грузок до любых точек конструкции. Или, иначе, при составлении уравнений ста­тики системы можно исходить из размеров недеформированного состояния. Такие системы называются геометрически линейными. Относительные деформации много меньше единицы, а потому их произведения и степени при выводе уравнений перемещений можно отбрасывать, как величины вто­рого порядка малости.

3. Материал обладает идеальной упругостью, то есть способностью полностью восстанавливать первоначальные размеры и форму после устранения причин, вы­звавших его деформацию. Деформации материала элемента конструкции в каждой его точке прямо пропорциональны напряжениям в этой точке, или, по - другому, подчиня­ются закону Гука, который впервые сформулировал это положение. Такой материал называется линейно-упругим. Конструкции, материал которых линейно-упругий, называются физически линейными.

4. Принцип независимости действия сил или принцип суперпозиции. Перемещения и напряжения упругого тела не зависят от последовательности нагружения тела, а определя­ются только конечным состоянием нагрузок. Результат действия группы сил равен сумме (алгебраической или геометрической) результатов, полученных от действия каждой силы в отдельности. Эта гипотеза справедлива только при условии действия двух предыдущих гипо­тез, т. е. для физически и геометрически линейных систем.

5. Гипотеза плоских сечений. Сечения плоские и перпендикулярные к оси бруса до деформации остаются плоскими и перпендикулярными после деформации. Это по­ложение впервые сформулировал Бернулли. Гипотеза не оправдывается, например, при кручении брусьев некруглого сечения.

6. Принцип Сен-Венана. В точках твердого тела, достаточно удаленных от места приложения внешних нагрузок на малой поверхности тела, напряжения почти не зави­сят от их распределения по этой малой поверхности, а зависят только от главного век­тора и главного момента заданных сил.

Это наглядно видно на рис. 1.3, так на расстоянии х = 0 от точки приложения сосредоточенной силы F максимальное напряжение ,

при - и при − (см. рис. 1.3).

Достоинством любых гипотез в любых науках является существенное упрощение применяемого математического аппарата при выводе основных уравнений. Недостаток – в ограниченности выводов, сделанных на их основе. Выводы науки о сопротивлении материалов менее строги, более приближенные, а следовательно, и более ограничен­ные, чем выводы других наук, занимающихся вопросами теории расчетов на проч­ность, например, теории упругости.

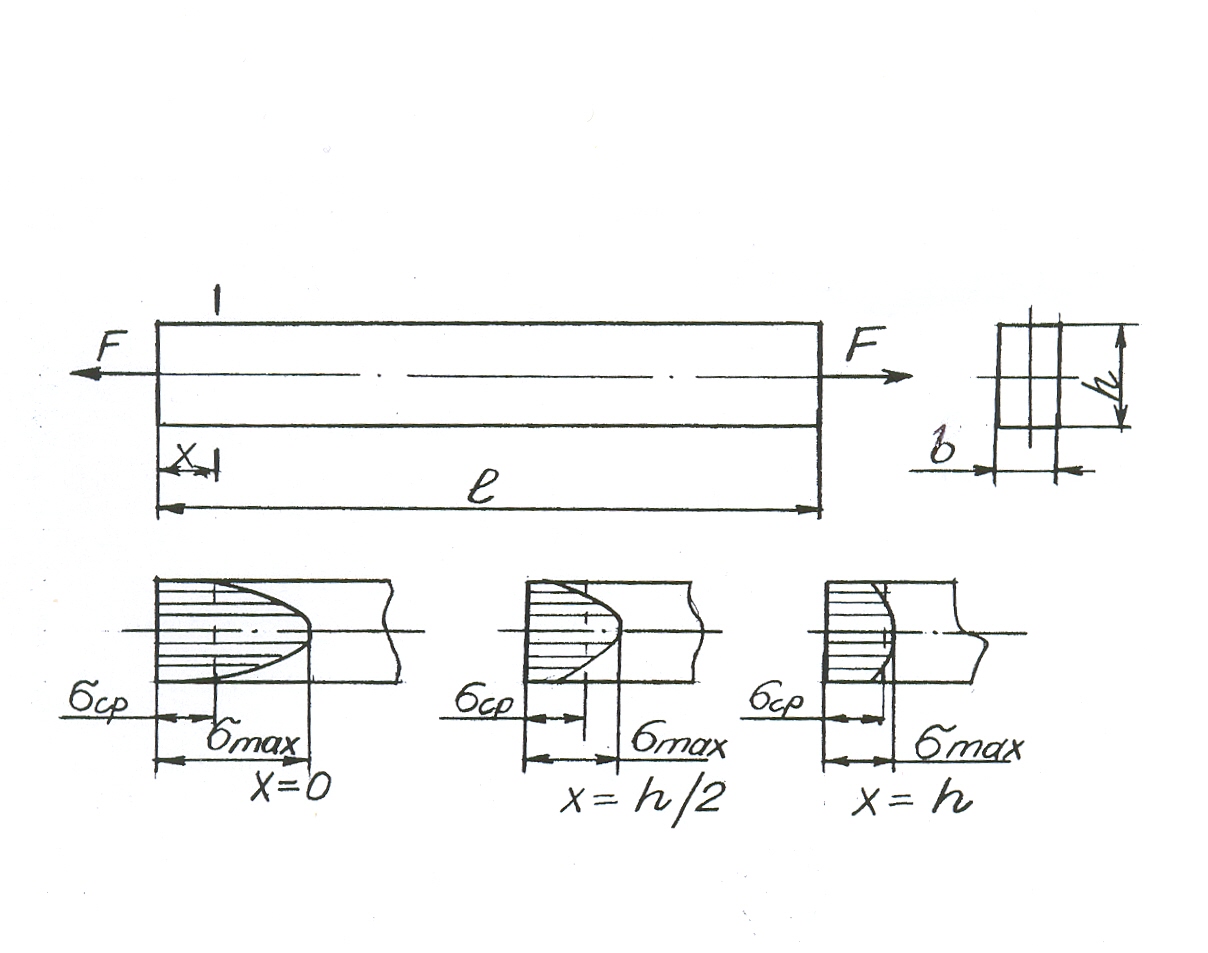
Рис. 1.3