Метод непосредственного интегрирования дифференциального уравнения изогнутой оси балки. Метод начальных параметров
Для балки, изображенной на рис. 9.1 имеем дифференциальное уравнение изогнутой оси
Двукратное интегрирование дает
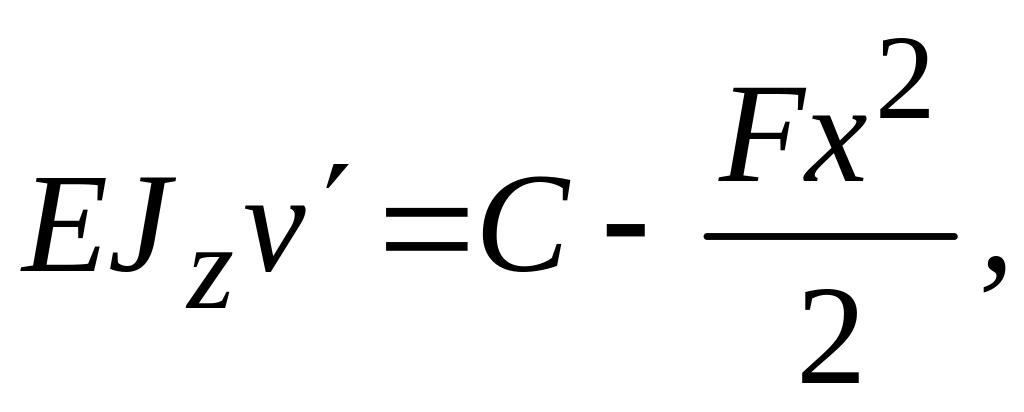
Постоянные
интегрирования
и
определим из граничных условий - условий
закрепления. В заделке (при
)
угол поворота и прогиб равны нулю, т. е.
имеем
Это позволяет записать
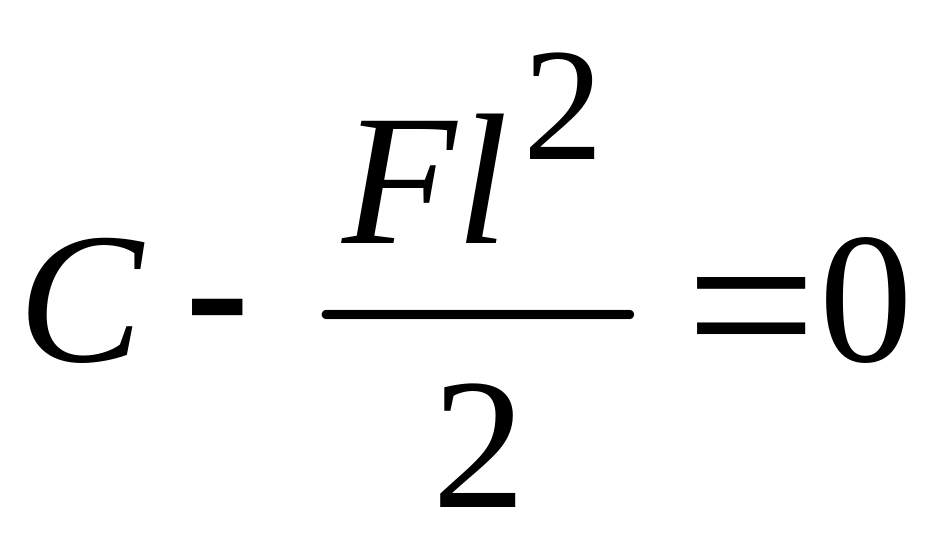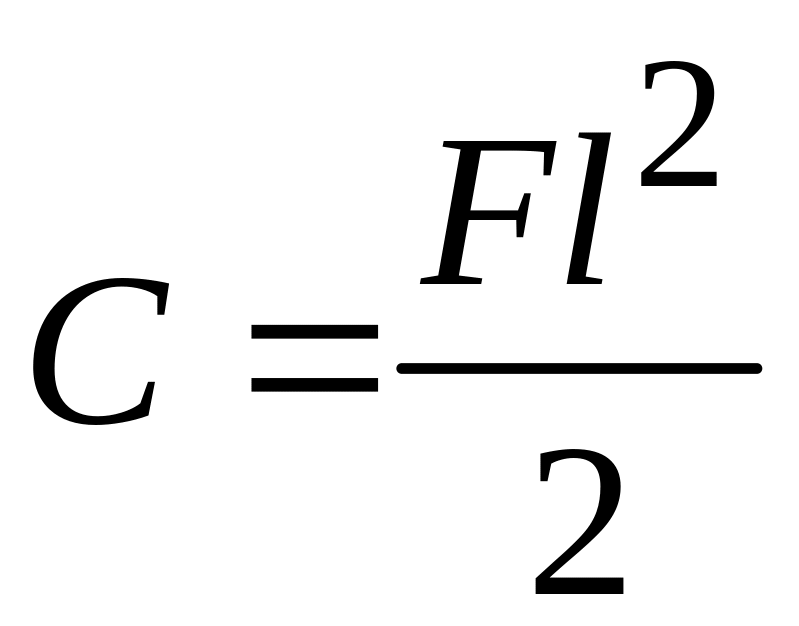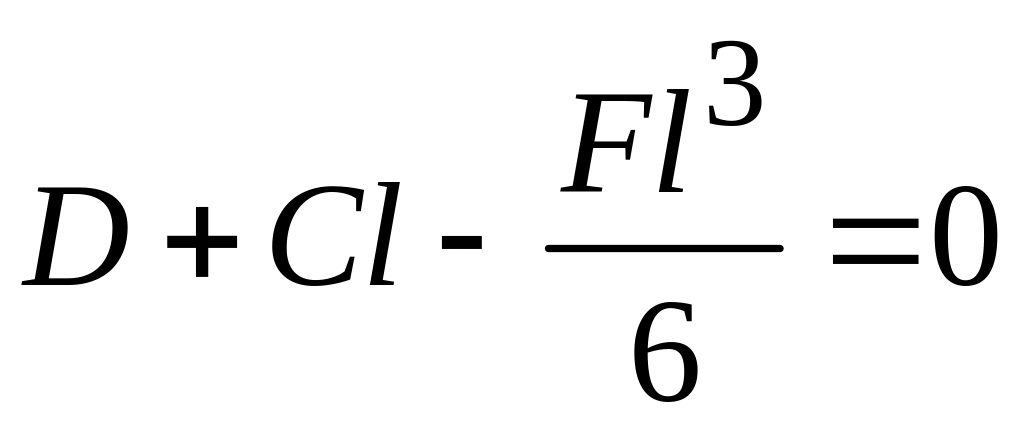и
;
и
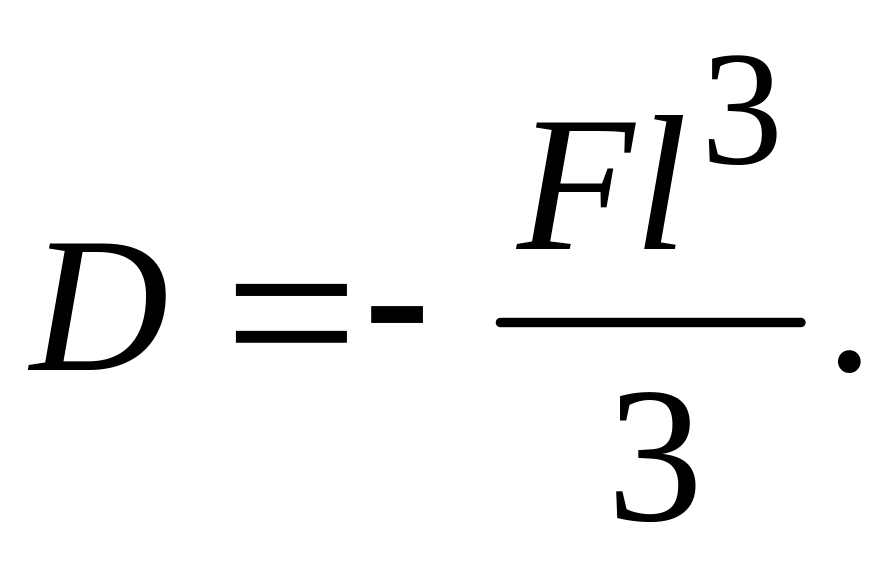С учетом найденных значений постоянных
интегрирования можно записать уравнения
углов поворота и прогибов
.
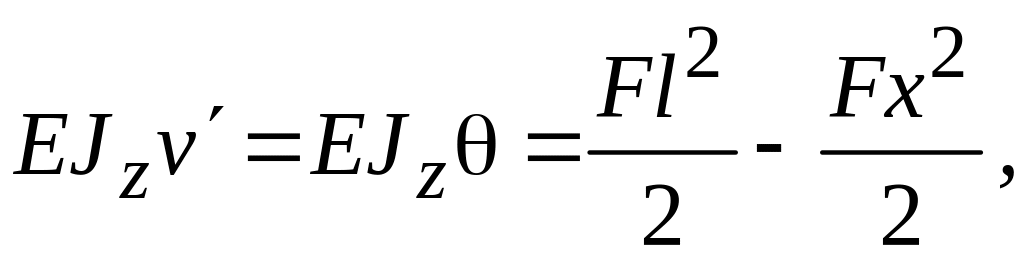
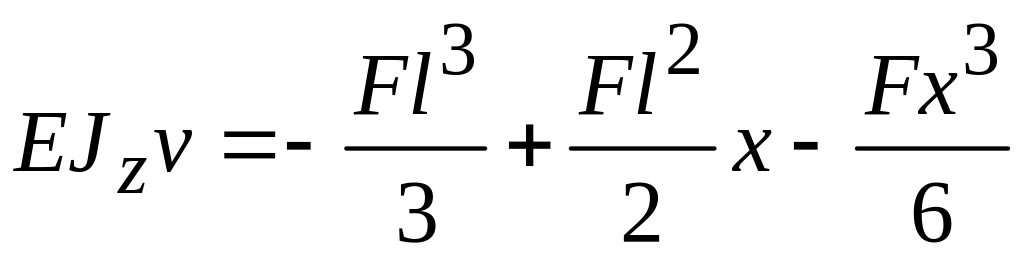В данном случае балка изгибается по параболе третьей степени.
В
более сложных случаях нельзя составить
единого выражения для изгибающего
момента для различных участков балки,
их количество для балки, содержащей
участков, будет равно количеству участков
балки. Интегрируя каждое из этих
уравнений, придем к необходимости
определить
постоянных интегрирования, что вызывает
некоторые затруднения в инженерных
расчетах. С целью снижения трудоёмкости
решения подобного рода задач применяется
такой метод составления дифференциальных
уравнений, когда
и
.
Упомянутый метод требует соблюдения
следующих правил:
1. Начало координат для всех участков балки следует брать в одной и той же точке на одном из концов балки. При этом следует иметь в виду, что при выборе начала координат на правом конце балки, при первом интегрировании дифференциального уравнения изогнутой оси балки знаки перед его слагаемыми надо изменить на противоположные, а при втором – вернуться к исходным. При составлении выражений изгибающего момента всегда следует рассматривать ту часть балки, которая содержит начало координат.
2.
Если распределенная нагрузка интенсивностью
обрывается на расстоянии
от начала координат, то ее необходимо
искусственно продлить до конца балки.
Добавленную нагрузку необходимо
уравновесить другой распределенной
нагрузкой, направленной в противоположную
сторону и имеющую ту же интенсивность
.
В этом случае на участках балки при
в выражение изгибающего момента будут
входить слагаемые последующих участков
точно в таком же виде, что и в предыдущих.
3.
При наличии сосредоточенного момента
на
расстоянии
от начала координат его следует умножить
на плечо
в выражении изгибающего момента для
участков при
.
4. Интегрирование дифференциальных уравнений должно производиться без раскрытия скобок.
Рассматривая условия неразрывности и плавности упругой линии на стыке участков балки, нетрудно убедиться, что при таком способе составления и интегрирования уравнений постоянные интегрирования уравниваются.
Докажем справедливость метода на следующем примере (рис. 8.2).
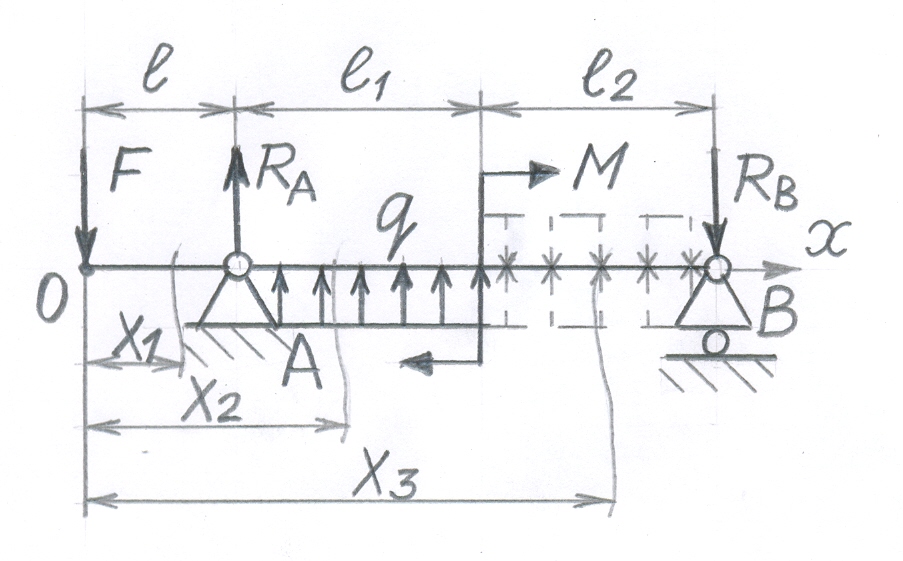
Рис. 9.2
За
начало координат выбираем сечение
левого конца балки. Для первого участка
(при
)
получим
,
,
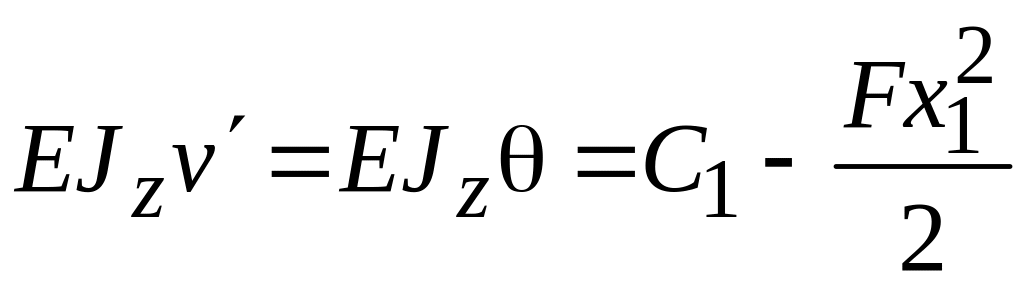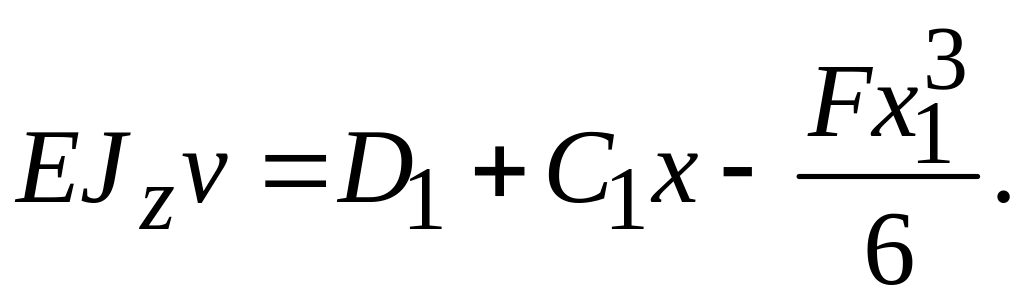
Для
второго участка (при
)
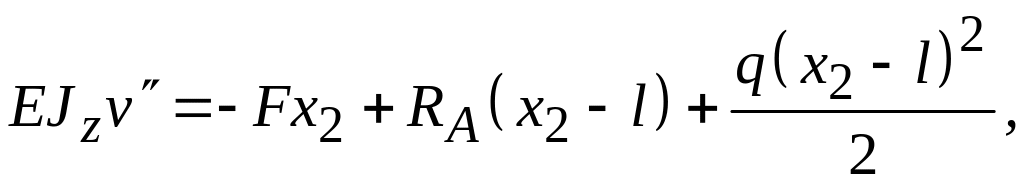
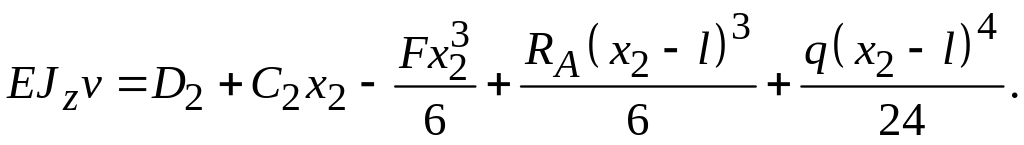
Для
третьего участка (при
)
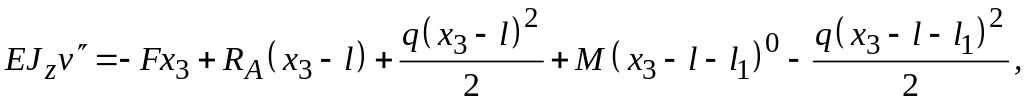
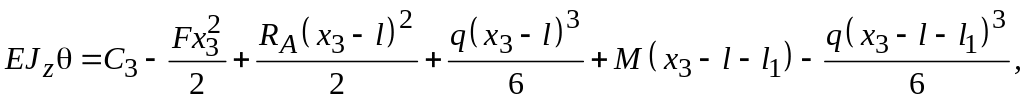
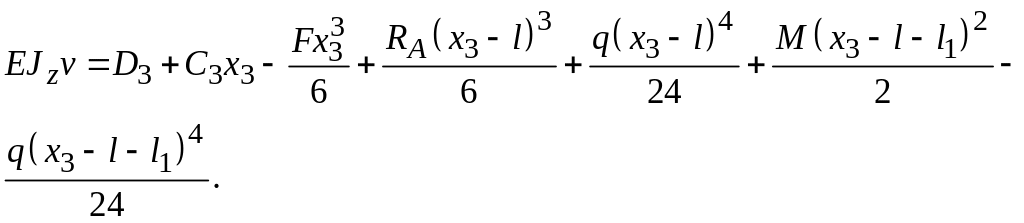
Получили
шесть неизвестных постоянных
интегрирования:
и
,
для нахождения которых необходимо
составление шести уравнений. Первые
два уравнения составим из условий
закрепления
1)
2)
.
Последние четыре уравнения составим из условия, что на стыке участков упругая линия не терпит разрывов, поэтому угол поворота сечений и прогиб будут одинаковыми
3)
4)
5)
5)
Рассмотрим подробнее условие (3)
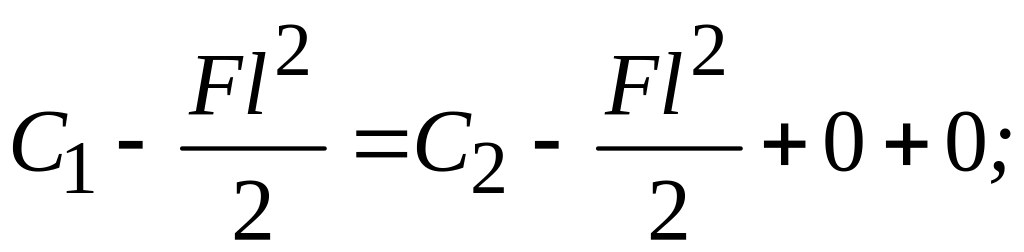откуда
следует, что
Из условия (5) следует
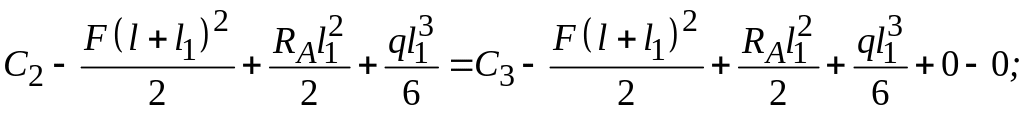
откуда
следует, что
или окончательно
Аналогично,
рассмотрев условия (4) и (6), мы найдем,
что
Значения и найдем из условий (1) и (2)
Вычтем из уравнения (2) уравнение (1)
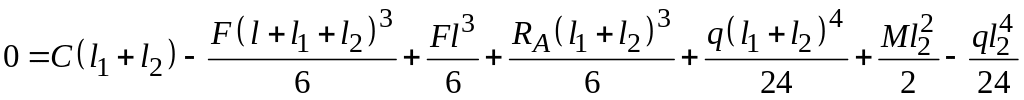и
решим его относительно
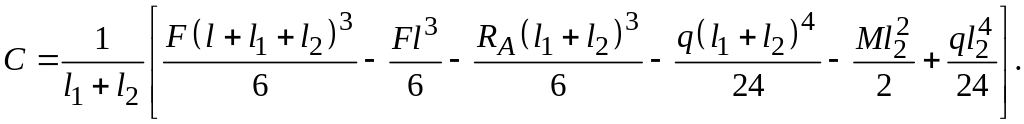
Подставив полученное значение в условие (1) найдем значение .
Таким образом, мы доказали, что при соблюдении правил метода при любом количестве участков балки количество постоянных интегрирования сводится к двум постоянным: и . Учитывая, что при использовании метода уравнивания постоянных, уравнения последующих участков всегда содержат слагаемые предыдущих участков, можно составить единые уравнения для всей балки:
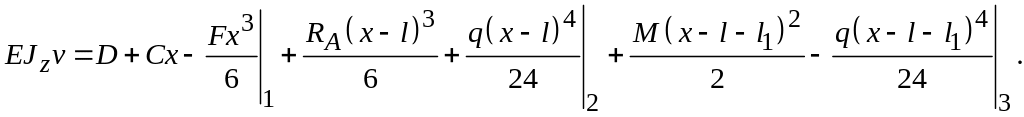
Здесь
все записанное до символа «
»,
относится к первому участку (при
),
стоящие ранее символа «
»
- ко второму (при
)
и стоящие ранее символа «
»
- к третьему (при
).
Запись единых уравнений для всей балки носит название метода начальных параметров; запись уравнений для каждого участка в отдельности – метода непосредственного интегрирования.