7.2. Расчет симметричных гибких нитей
Выясним,
что произойдет с симметричной нитью
(точки подвеса находятся на одном уровне)
длиной L,
перекрывающей пролет длиной l,
если после подвешивания ее температура
изменится на
.
Удлинение (укорачивание) нити, вызванное
изменением температуры, будет равно
,
где
- коэффициент линейного температурного
расширения. При повышении температуры
нить удлиняется. В связи с этим увеличится
ее стрела провисания и, как следствие,
уменьшится ее натяжение. При понижении
температуры произойдет обратное явление.
Изменение длины нити, вызванное ее
натяжением, будет, согласно закону Гука,
равно:
.
Обозначим разность между длиной нити
и длиной пролета
.
Тогда зависимость между изменениями
длины нити и силой натяжения нити можно
выразить системой уравнений
,
(7.5)
Система
уравнений (7.5) дает возможность определить
две величины из трех:
,
если одна из них задана.
Исключив
из уравнений (7.5) силу натяжения
,
получим
.
(7.6)
Полученное уравнение позволяет решать следующие две задачи.
Задача
1(прямая).
Какова должна быть разность
между длиной нити и длиной пролета,
чтобы стрела провеса при сезонных
колебаниях температуры
не превосходила заданной величины
?
Решение прямой задачи из уравнения (7.6) дает:
.
(7.7)
Задача
2 (обратная).
Нить начальной длины начальной длины
подвешена в двух точках, пролет между
которыми равен
.
Найти максимальную стрелу провеса при
сезонных колебаниях температуры
.
Решение обратной задачи получается как подходящий корень кубического уравнения
.
(7.8)
Уравнение удобно решать с использованием приближенных методов вычисления, либо с использованием приложения Mathcad.
Вопросы для самопроверки
1. Допущения, принятые при расчете гибких нитей. Их влияние на точность расчетов.
2. Запишите условие прочности для гибкой нити.
3. Сформулируйте два основных типа задач, встречающихся при расчете проводов и тросов.
Лекция № 8 плоский изгиб, расчет на прочность
8.1. Основные понятия
Изгиб
– вид деформации стержня, при котором
в его поперечных сечениях возникают
изгибающие моменты. В большинстве
случаев одновременно с изгибающими
моментами
возникают и перерезывающие силы
и
Ранее, при рассмотрении внутренних
силовых факторов, было установлено, что
перерезывающие силы являются
равнодействующими внутренних касательных
сил, возникающих в поперечных сечениях:
Изгибающие моменты – результирующие
моменты внутренних нормальных сил,
возникающих в поперечном сечении,
относительно нейтральной линии этого
сечения:
В случае, если перерезывающие силы в
сечениях равны нулю и действуют только
изгибающие моменты, изгиб называется
чистым.
В случае, если ни изгибающие моменты,
ни перерезывающие силы не равны нулю,
изгиб называется поперечным.
С геометрической точки зрения изгиб характеризуется тем, что ось стержня прямолинейная до деформации становится криволинейной. Для кривого стержня изгиб связан с изменением радиуса кривизны стержня.
Деформация изгиба возникает при нагружении стержня силами, действующими в плоскостях, проходящих через его продольную ось и перпендикулярными этой оси, а также парами сил (моментами), действующими в тех же плоскостях. В случае, если все нагрузки действуют в одной плоскости изгиб называют плоским, а плоскость действия сил – силовой плоскостью (рис. 8.1).
Мы ограничимся рассмотрением стержней, поперечные сечения которых имеют хотя бы одну центральную ось симметрии, допустим ось У. Тогда ось У, и
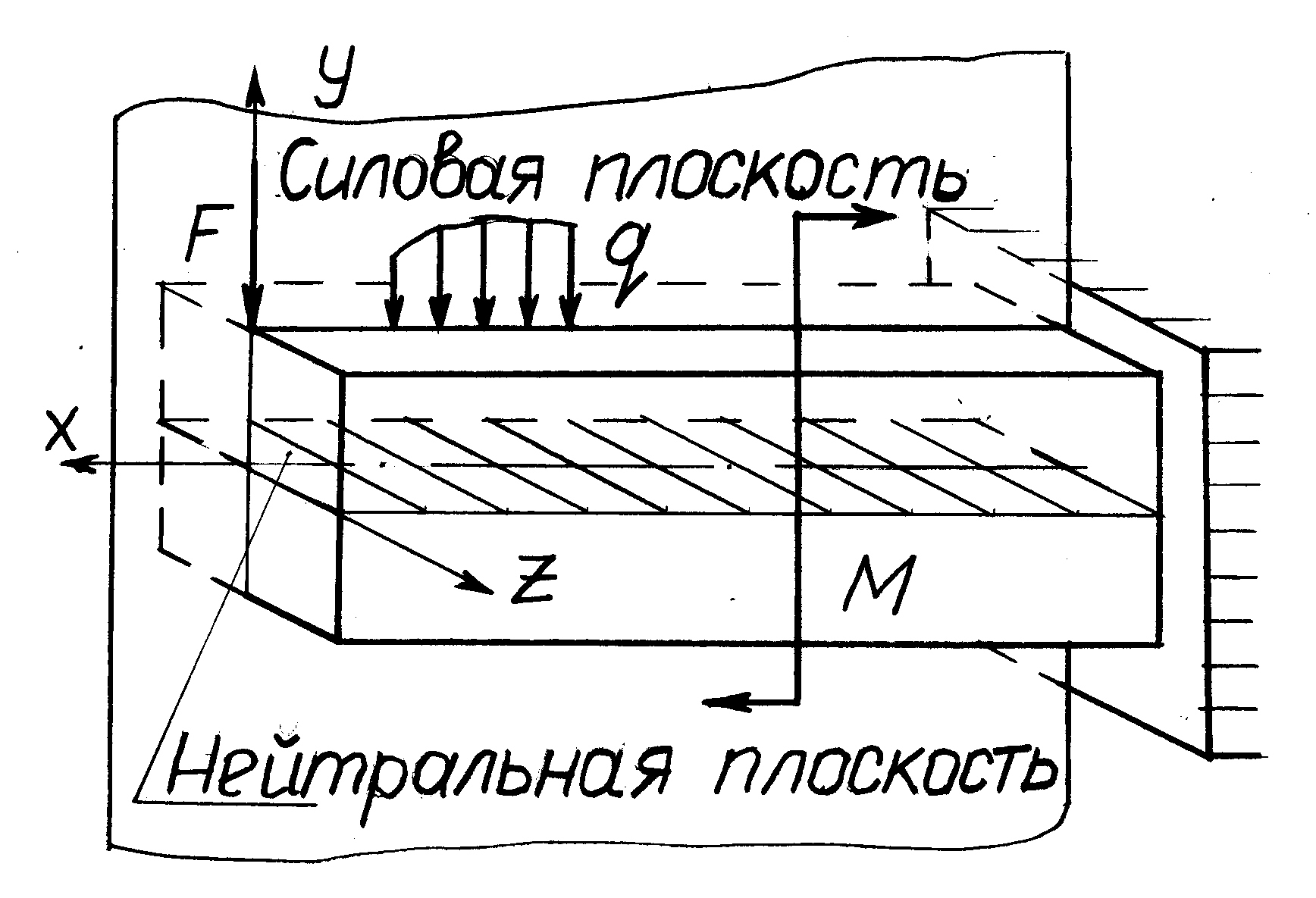
Рис. 7.1
перпендикулярная
ей ось
Z
будут главными центральными осями (
).
Плоскость, проходящая через продольную
ось стержня и одну из ее главных
центральных осей, называют главной
плоскостью стержня.
Если силовая плоскость совпадает с
одной из главных плоскостей, то имеет
место прямой
изгиб.
При прямом изгибе изогнутая ось стержня
располагается в силовой плоскости.
Линя пересечения силовой плоскости с плоскостью поперечного сечения называется силовой линией.
Если силовая плоскость не совпадает ни с одной из главных плоскостей стержня, или, что то же самое, силовая линия не совпадает ни с одной из главных центральных осей поперечного сечения, то изгиб называется косым. Свое название он получил из-за не совпадения силовой плоскости и плоскости, в которой лежит изогнутая ось бруса.
Очевидно, и это подтверждается практикой, что при изгибе часть волокон стержня испытывают растяжение, а часть – сжатие. Границей между областями, испытывающими растяжение и сжатие является слой волокон, который лишь искривляется не испытывая при этом ни растяжения ни сжатия. Этот слой волокон носит название нейтрального слоя. Линия, по которой пересекается нейтральный слой с поперечным сечением, называется нейтральной линией (нулевой линией).
Стержни, работающие в основном на изгиб, принято называть балками. Часть балки, находящаяся между опорами, называют пролетом. Части балки, расположенные по одну сторону от опоры, называют консолями.