Лекция № 7 расчет гибких нитей (проводов)

7.1. Гибкая нить под действием распределенной нагрузки

Большой интерес в инженерной практике представляют задачи, связанные с расчетом проводов линий электрических передач, тросов и канатов подвесных дорог, мостов и перекрытий.

Пусть (рис. 7.1) имеется гибкая нить постоянного сечения, нагруженная собственным весом и подвешенная в двух точках, находящихся на разных уровнях. Под действием собственного веса нить провиснет по некоторой кривой АОВ.

Горизонтальная проекция кривой равна расстоянию между опорами, т. е пролету длиной l. Вес нити равномерно распределен по ее длине. Обычно провисание нити невелико по сравнению с ее пролетом, и длина кривой АОВ мало отличается (не более 10%) от длины хорды AB. В этом случае с достаточной степенью точности можно считать, что вес нити равномерно распределен, не по ее длине, а по длине ее проекции на горизонтальную ось, т. е. вдоль пролета l. Эта равномерно распределенная нагрузка q может включать в себя не только собственный вес, но и вес льда или любой другой нагрузки.

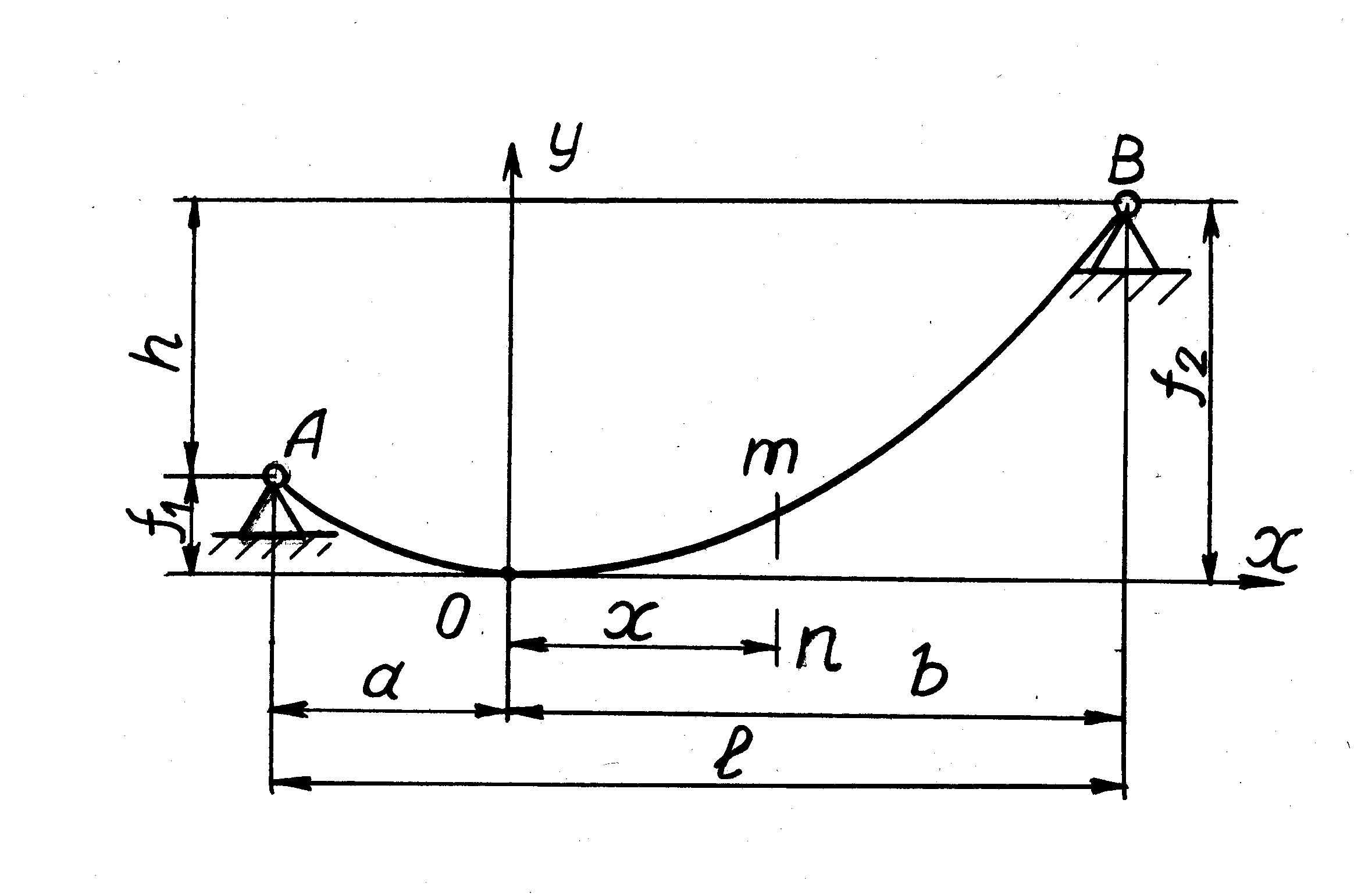
Рис. 7.1

Сделанное допущение о законе распределения нагрузки существенно облегчает расчет, но делает его вместе с тем приближенным. Точные подсчеты показывают, что значение погрешности зависит от отношения провисания нити к длине пролета. При отношении погрешность не превосходит 0,3% , при составляет 1,3%, а при погрешность несколько превосходит 5%.

Выберем в самой низшей точке провисания нити О начало координат. Очевидно, что в точке О касательная к кривой повисания нити горизонтальна. По этой касательной направим вправо ось x. Положение точки О нам пока неизвестно. Ее положение зависит от величины нагрузки q, от соотношения длины нити по кривой L и длиной пролета l, а также от относительного положения опор.

Вырежем двумя сечениями – в начале координат и на расстоянии x от начала координат (сечение m – n) часть длины нити (Рис. 2).

Гибкая нить способна сопротивляться только растяжению, т. е. в виде сил (H и T), направленных по касательным к кривой и заменяющих действие отброшенных частей.

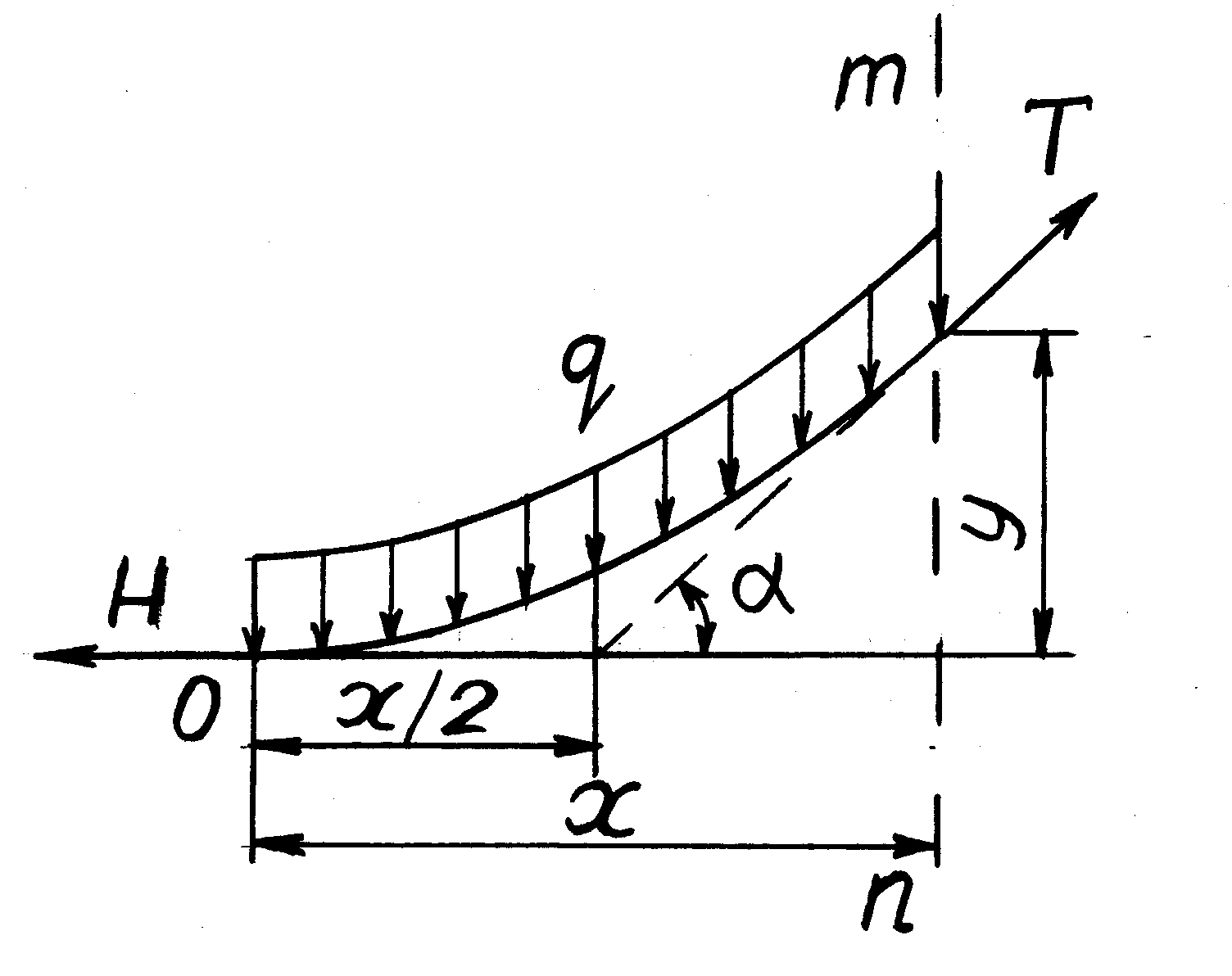
Рис. 7.2

Составим уравнение равновесия вырезанного участка нити. Возьмем сумму моментов всех сил относительно точки приложения силы T и приравняем ее нулю. Тогд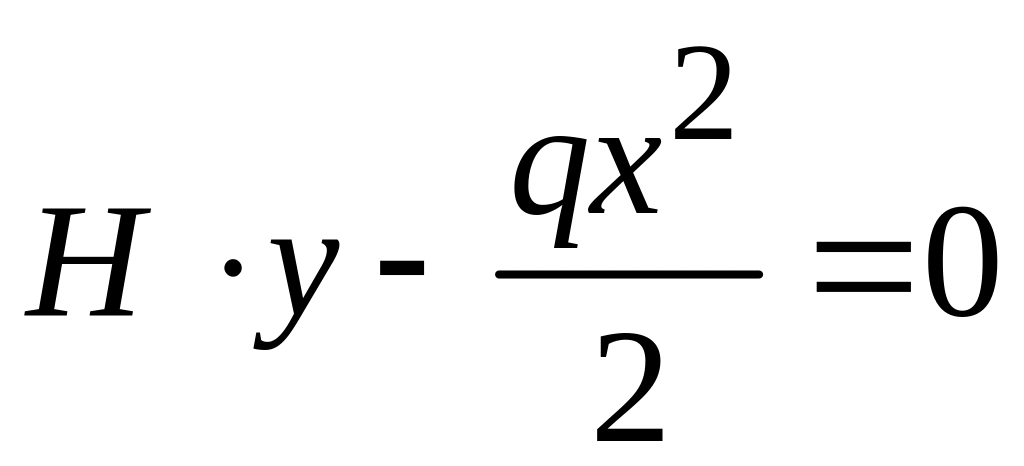а , откуда

(7.1)

Отсюда следует, что кривая провисания нити является параболой. Когда обе точки подвеса нити находятся на одном уровне, то , а и . Получаем:

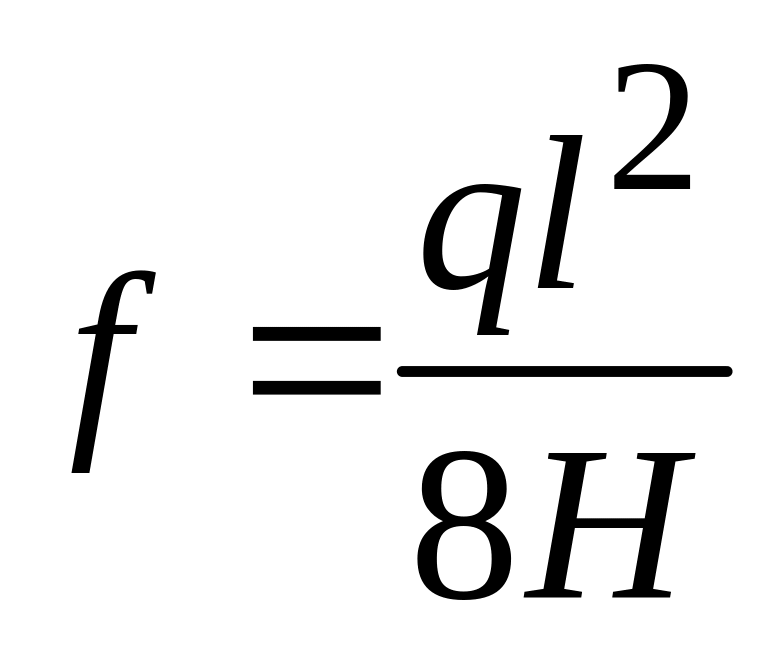(7.2)

Из этой формулы находим величину силы H:

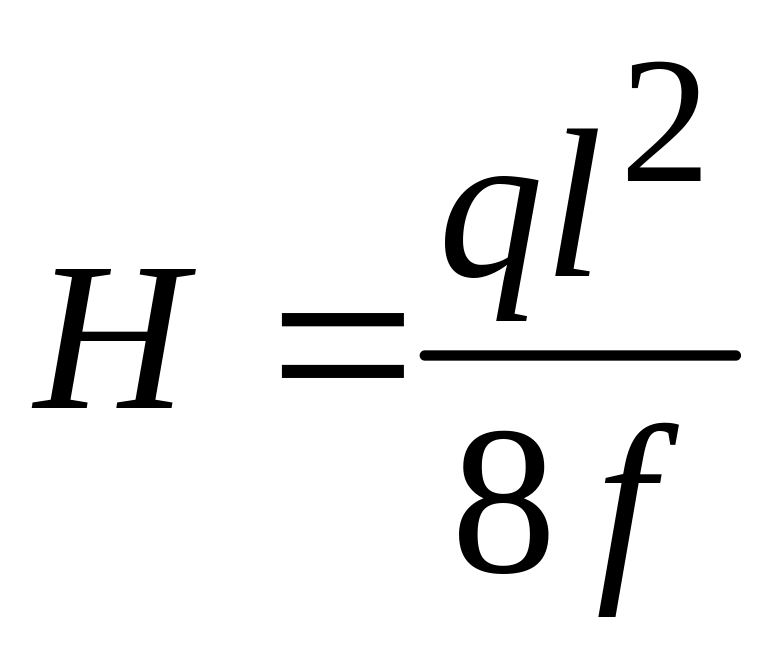(7.3)

Величина Н называется горизонтальным натяжением нити. Длину нити по кривой провисания можно вычислить по известной из математики приближенной формулы .

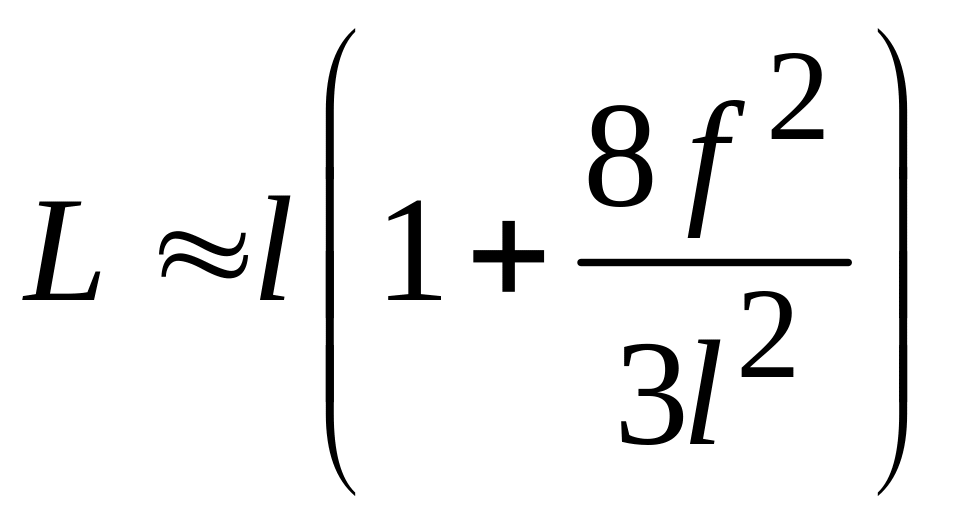Составим еще одно условие равновесия вырезанной части нити, а, именно, приравняем нулю сумму проекций всех сил на ось x:

.

Из этого уравнения найдем силу натяжения нити в произвольной точке

.

Отсюда следует, что сила Т увеличивается от низшей точки нити к опорам и будет наибольшей в точках подвеса – там, где касательная к кривой провисания нити составляет наибольший угол с горизонталью. При малом провисании нити этот угол не достигает больших значений, поэтому с достаточной для практики степенью точности можно считать, что усилие в нити постоянно и равно ее натяжению Н. Для симметричной нити точное значение максимальной силы натяжения в опорах можно определить следующим образом. Вертикальные составляющие реакций опор равны между собой и равны , а горизонтальные составляющие равны силе Н, определяемой по формуле (7.3). Полные реакции опор получатся как геометрические суммы этих составляющих:

.

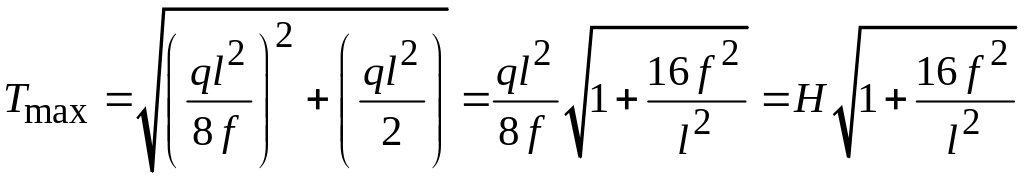Условие прочности для гибкой нити, если через А обозначена площадь сечения, имеет вид:

.

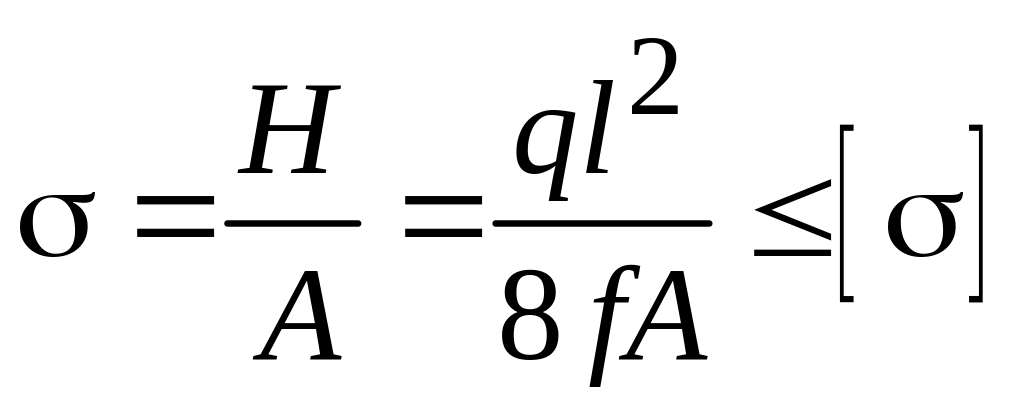Из этой формулы при заданных можно определить необходимую стрелу провисания . Решение упростится, если в включен лишь собственный вес; тогда , где - вес единицы объема материала нити

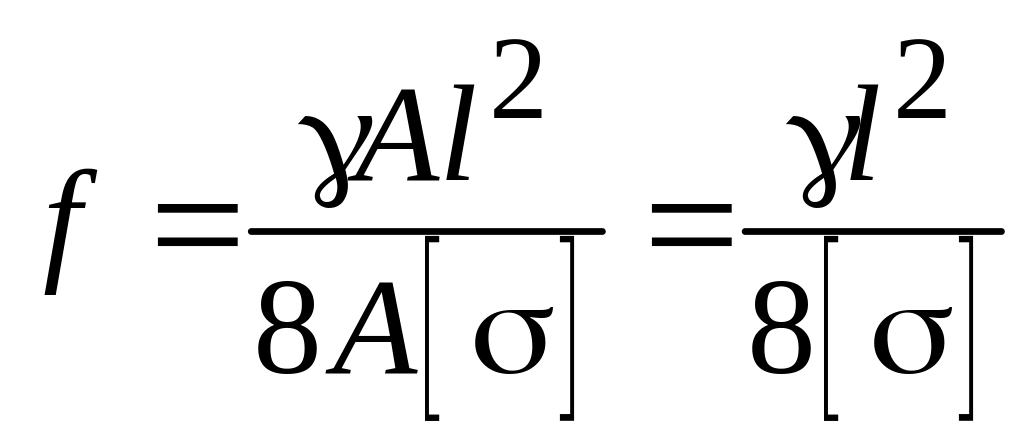, т. е. величина А не войдет в расчет.

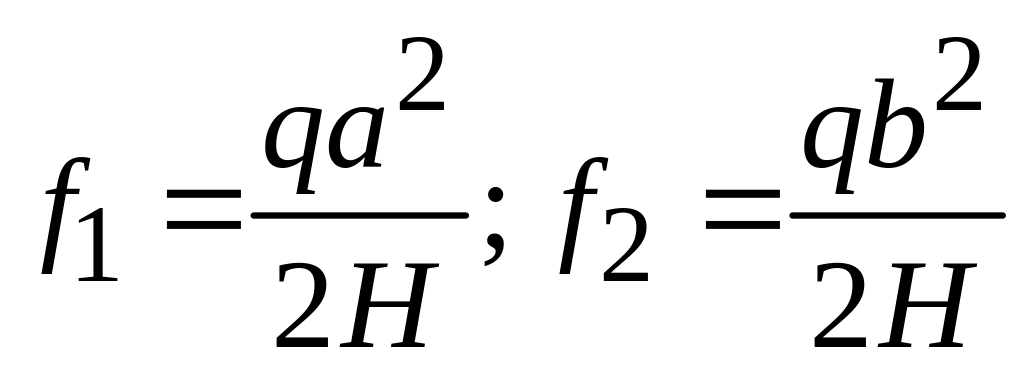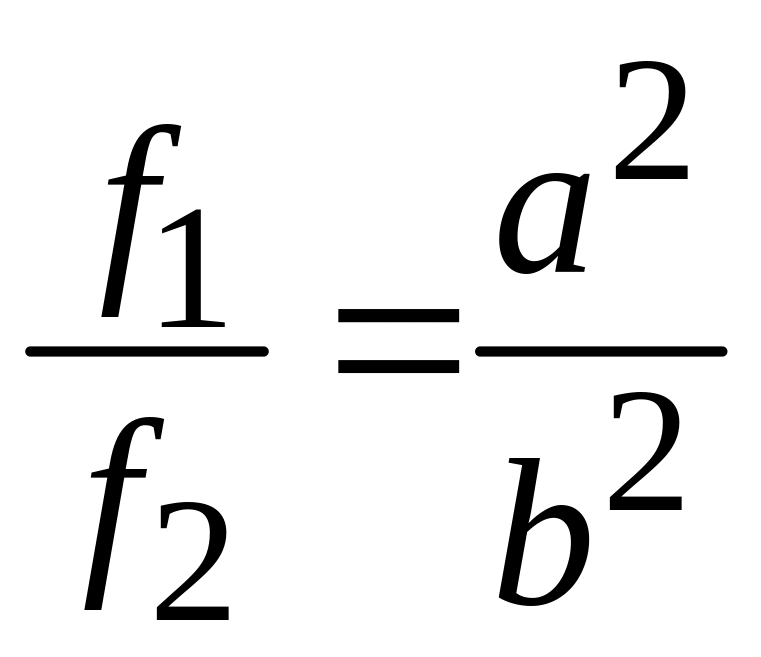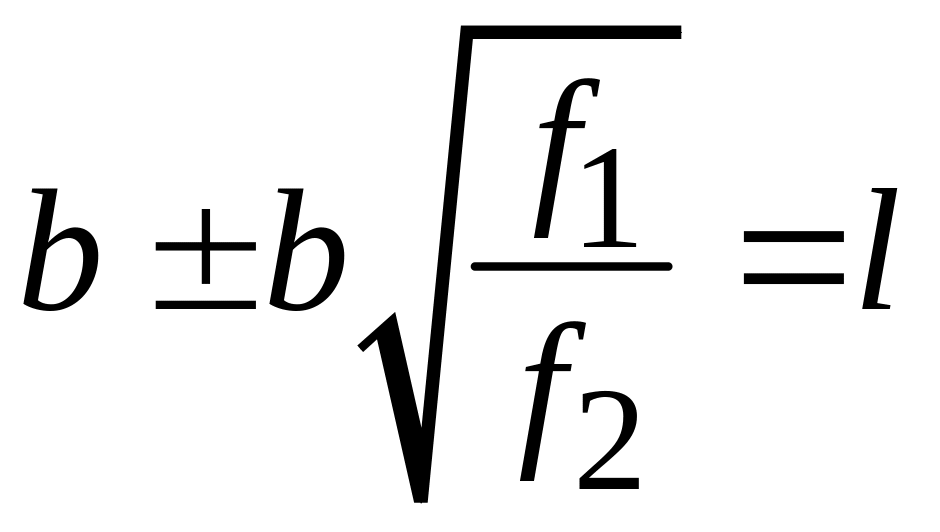Если точки подвеса нити находятся на разных уровнях, то, подставляя в уравнение (7.1) значения и находим: и деля первое на второе, находим: или . Так как , то или 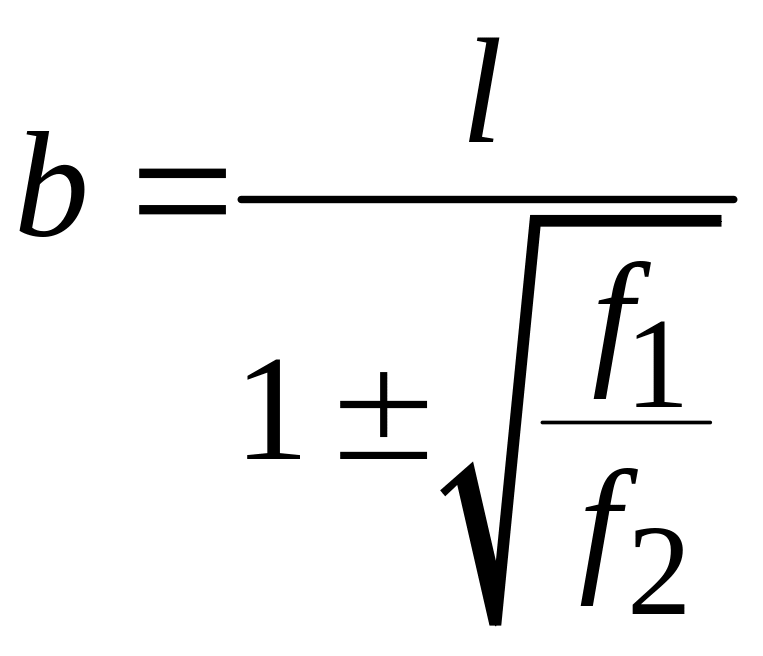. Подставляя это значение в формулу 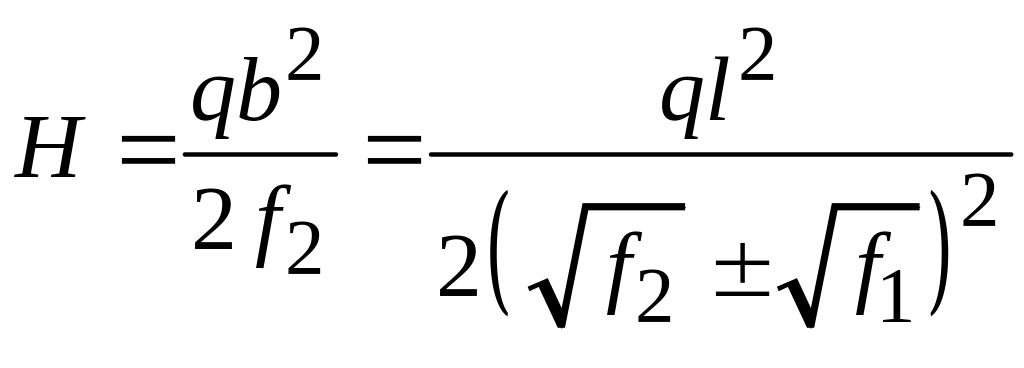(7.4)

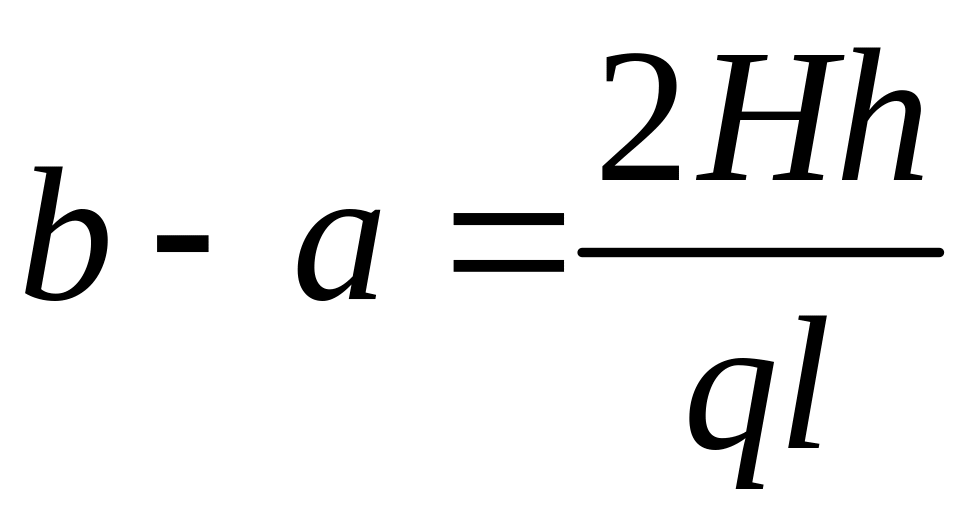Так как разность уровней подвески , то или и 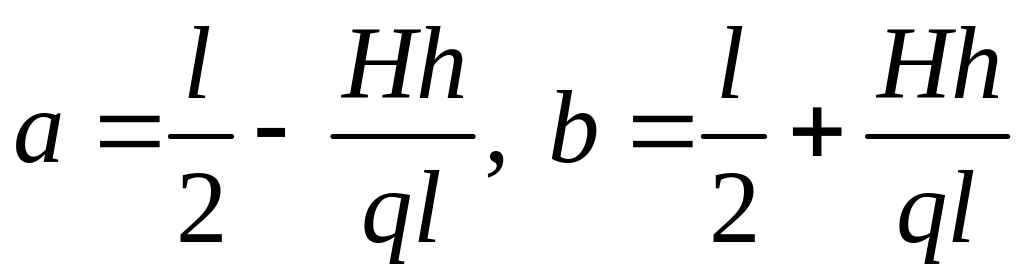. При а>0 в формуле (7.4) перед вторым корнем берется знак плюс при а<0 - знак минус. Подставляя полученные значения а и b для стрел провисания и , получим:

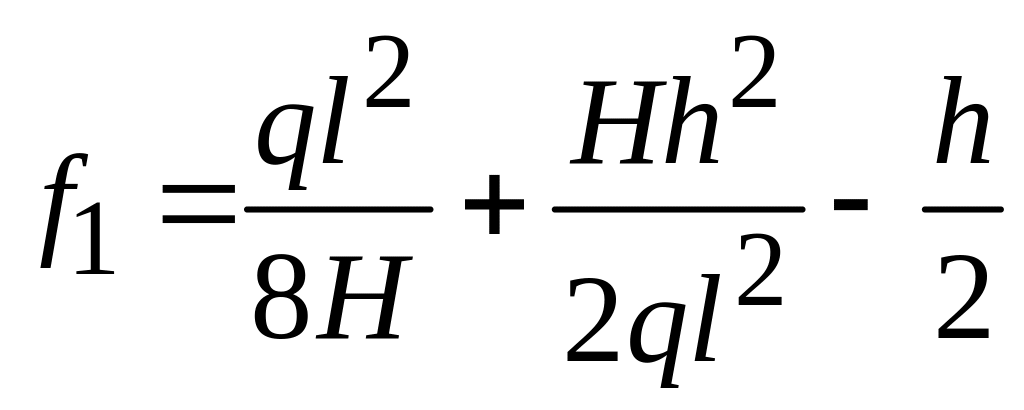и .
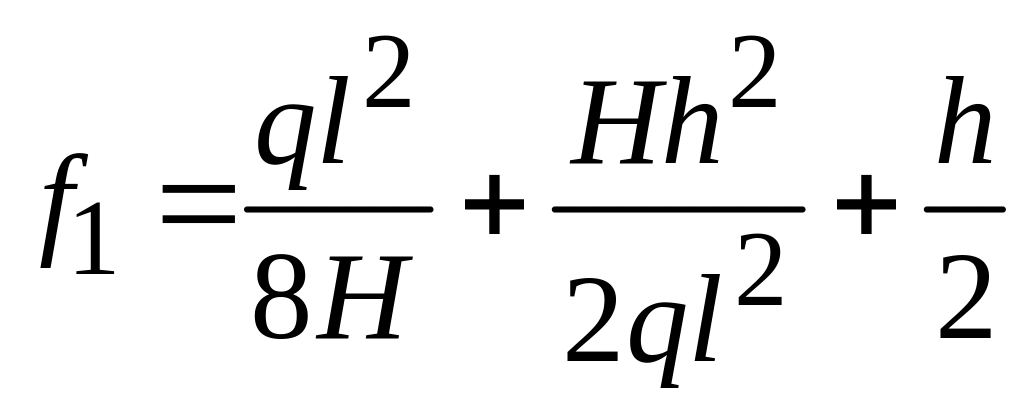