6.4. Предельное состояние. Расчеты на прочность и жесткость

Как показывают эксперименты, стадии перехода от линейно упругого деформирования к упругопластическому деформированию и разрушению для данного материала совершается при одном и том же значении нормального напряжения. Поэтому напряжение может рассматриваться в качестве критерия перехода материала от одной степени его «нагруженности» к другой.

Состояние элемента конструкции, при котором не возможна его дальнейшая эксплуатация, называется предельным состоянием. Предельное состояние может наступить по причине потери несущей способности конструкции либо по причине ее не соответствия техническим требованиям. В сопротивлении материалов изучают первую из перечисленных причин. Каждому предельному состоянию соответствует свое предельное напряжение .

Для пластичных материалов предельное состояние, по причине потери несущей способности конструкции, наступает при достижении предела текучести , для хрупких – при достижении предела прочности . Эксплуатировать конструкции при напряжениях, равных предельным, не допустимо. Это связано с тем, что любой конструкционный материал имеет некоторый разброс по характеристикам прочности. Кроме того, предельное состояние не должно наступать в течение всего срока эксплуатации конструкции, которая может иногда подвергаться нагрузкам, превышающим нормативные. Поэтому нужен некоторый запас на всякого рода случайности, т. е.

(6.5)

где - нормативный коэффициент запаса;

- допускаемое напряжение.

Для деформации растяжения – сжатие условие прочности имеет вид

. (6.6)

Для пластичных материалов , где нормативный коэффициент запаса в зависимости от условий эксплуатации и назначения конструкции.

Для хрупких материалов .

В инженерной практике имеют дело с тремя типами задач: проверочный расчет, проектный расчет и определение максимальной нагрузки. Проверочный расчет проводится по формуле (6.8). Проектный расчет - по формуле . Определение максимальной нагрузки – по формуле

Расчет на жесткость при деформации растяжения – сжатия проводится по формуле

, (6.7)

- допускаемая абсолютная деформация.

Жесткость конструкции не зависит от прочности материала, а только от его модуля упругости. Для сталей, у которых модуль упругости практически одинаковый для всех марок, безразлично какую сталь использовать в конструкции - дорогую высоколегированную и высокопрочную или дешевую углеродистую.

6.5. Термические напряжения и деформации

Инженерам теплоэнергетикам в своей практической деятельности часто приходится сталкиваться с необходимостью учета температурных удлинений трубопроводов для различных энергоносителей (например, пара, горячей воды, горячих газов и др.). Если концы трубопровода жестко закреплены и он не может изменять длину с изменением температуры, то в его материале возникает термичское напряжение При площади поперечного сечения трубопровода А, нагреваемый (охлаждаемый) трубопровод окажется сжатым (растянутым) силой . Из этих формул следует практически важный вывод: напряжение и усилие, возникающее в жестко закрепленном участке трубопровода не зависят от его длины, а только от разности температур, а усилие и от площади поперечного сечения. Это усилие не должно передаваться на сосуды и аппараты, в которые подается энергоноситель, а восприниматься жесткими концевыми опорами, между которыми трубопровод может поддерживаться промежуточными подвижными опорами. Это требование установлено нормативно-технической документацией.

Для стального трубопровода с наружным диаметром мм и внутренним мм при перепаде температур С и коэффициенте линейного расширения стали α=1,2 1/⁰ С усилие, передаваемое на опоры,

=651,1кН или более 65 тонн.

Для стальных трубопроводов с допускаемым напряжением МПа, предельная разность температур, при которой требуется установка компенсирующих устройств, С.

В случае, если температурные напряжения превосходят допускаемые, в конструкцию трубопровода необходимо вводить компенсатор – устройство, служащее для восприятия температурных деформаций. Среди различных типов компенсаторов, таких как линзовые, сальниковые, П - образные, S – образные и другие, наибольшее распространение получили П – образные компенсаторы. Для условных диаметров трубопроводов компенсирующая способность П – образных компенсаторов составляет = 20…350мм в зависимости от размера компенсатора. Компенсирующая способность компенсатора должна быть больше возможных абсолютных температурных деформаций трубопровода, т. е. .

Конструкция различных компенсаторов, их габаритно-присоединительные размеры и компенсирующая способность приводятся в соответствующей нормативно-технической документации. Необходимое количество компенсаторов на участке трубопровода определяется по формуле

,

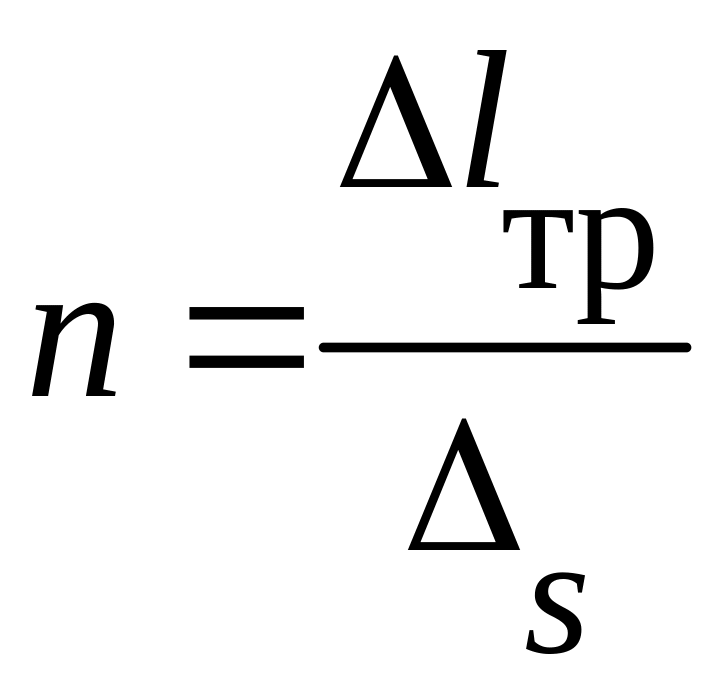
где и − длина участка трубопровода и его температурное удлинение; − компенсирующая способность одного компенсатора.

Вопросы для самопроверки

1. Какой вид нагружения бруса называется растяжением (сжатием)?

2. Как определяются нормальные напряжения в поперечных сечениях стержня?

3. Как определяются деформации и перемещения при растяжении и сжатии?

4. Как вычислить потенциальную энергию упругой деформации стержня при растяжении и сжатии?

5. Перечислите основные механические характеристики материалов, определяемые в опытах на растяжение и сжатие.

6. Приведите примеры пластичных и хрупких материалов.

7. Запишите условия прочности для пластичных и хрупких материалов.

8. Какие виды задач позволяет решать условие прочности?

9. Запишите формулу определения термических напряжений