6.2. Потенциальная энергия упругой деформации при растяжении и сжатии

При нагружении упругого тела внешние силы совершают работу W на перемещениях, которые получают точки их приложения. Если процесс нагружения совершают медленно (статически), то можно считать, что кинетическая энергия движения тела . В этом случае вся работа, если пренебречь рассеиванием энергии в окружающую среду, переходит в потенциальную энергию упругой деформации: .

Рассмотрим стержень, который растягивается в пределах упругих деформаций на величину (рис. 6.2).

Графически зависимость между силой F и деформацией представлена на рисунке прямой линией. В процессе нагружения сила возрастает от нуля до конечного значения. Этот процесс можно представить, как последовательность бесконечно малых приращений удлинений , вызываемой силой , которую на этом приращении можно считать постоянной. Следовательно, работа на перемещении равна или численно равна площади треугольника

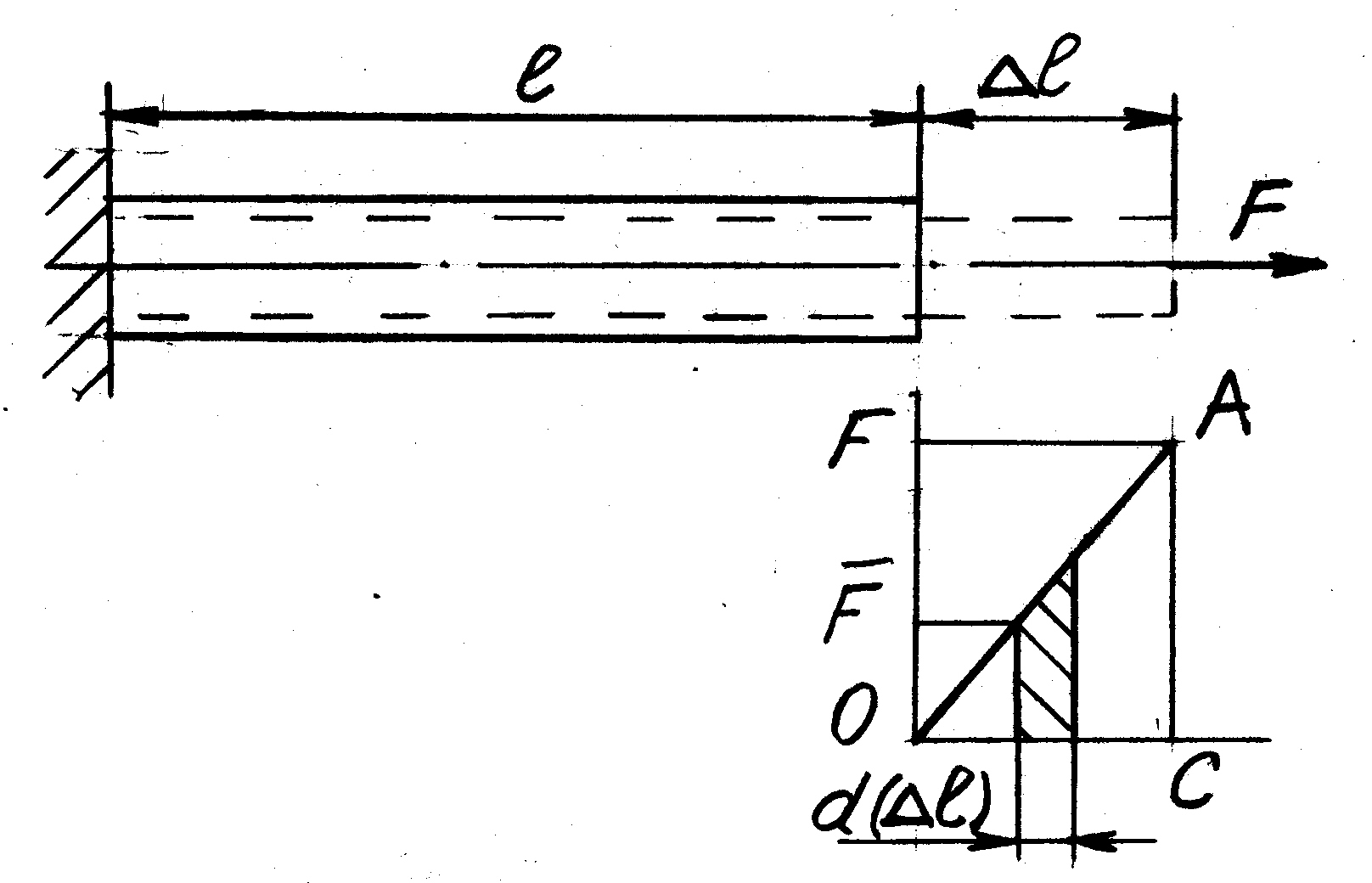
Рис.6.2

ОАС, т. е. половине произведения силы на вызываемое ей перемещение

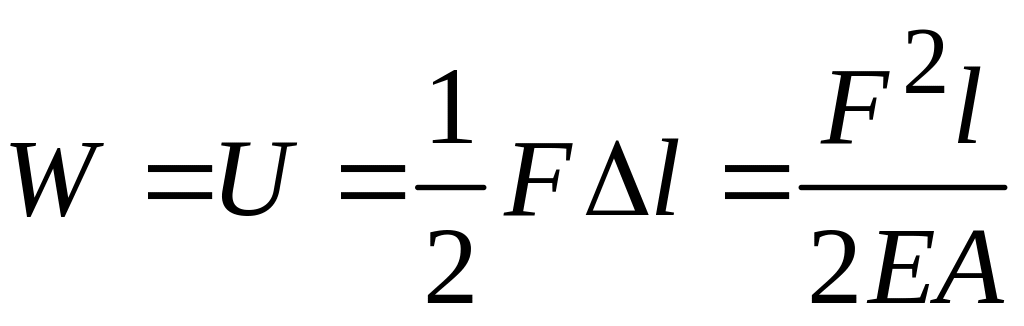(6.3)

Результат, полученный для деформации растяжения – сжатия, верен при любом другом виде деформации, т. е. работа любого силового фактора (силы, момента) равна половине произведения конечного значения силового фактора на конечное значение соответствующего перемещения. Это утверждение носит название, уже упомянутой ранее, теоремы Клайперона. При изгибе: силовой фактор – изгибающий момент, перемещение – угол поворота плоского сечения. При кручении: силовой фактор – крутящий момент, перемещение – угол закручивания.

Формулой (6.5) можно пользоваться только в случае, когда продольная сила и площадь поперечного сечения постоянны. В остальных случаях

(6.4)

Потенциальная энергия всегда положительная величина. При ее вычислении нельзя пользоваться принципом независимости действия сил, так как зависимость между N и U нелинейная.

Для оценки энергоёмкости материала в сопротивлении материалов пользуются понятием удельной потенциальной энергией деформации , где – объём стержня.

6.3. Механические испытания образцов материалов на растяжение и сжатие.

Сравнительные испытания различных конструкционных материалов преследуют следующие цели. Во-первых, дать конструкторским и проектным организациям усредненные в общегосударственном масштабе значения прочностных и деформационных характеристик для различных материалов. Во-вторых, для приемо-сдаточного контроля материалов на заводах-изготовителях. В-третьих, для контроля качества материалов на промежуточных стадиях изготовления сложных деталей, когда имеет место разного рода физико-химические виды его обработки.

Для сопоставимости результатов испытаний, полученных в разных лабораториях, их проводят на стандартных образцах в стандартных условиях нагружения и методов обработки полученных результатов (ГОСТ 1497-84). Испытания проводят как на цилиндрических, так и на плоских образцах. Наибольшее распространение получили цилиндрические образцы с отношением (см. рис. 6.3), где . Для прямоугольных образцов их эквивалентный диаметр подсчитывается по формуле . Применяются так же короткие образцы с отношением При испытании на сжатие используется кубики или цилиндрические образцы, высота которых

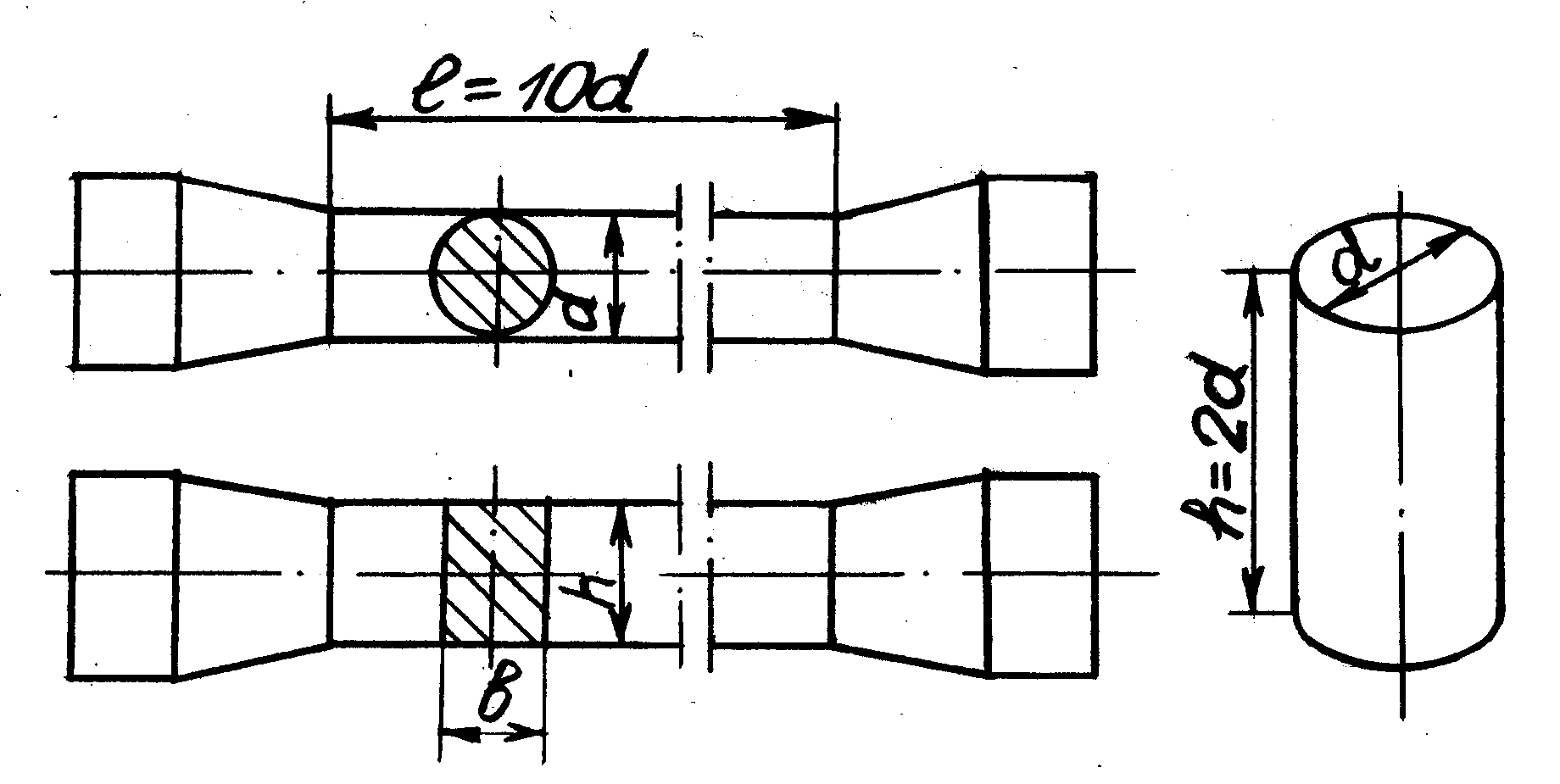
Рис. 6.3

Испытания проводят на разрывных машинах. Передача усилия на образец осуществляется через захваты. Взаимное движение захватов чаще всего производится через механическую передачу (винт-гайка) или гидравлическую систему. Как правило, разрывная машина должна содержать устройства для измерения прикладываемой к образцу силы и его деформации; а также графопостроитель, который вычерчивает на бумаге зависимость усилия F от абсолютной деформации . Для удобства сравнения результатов испытаний и их анализа зависимость заменяют зависимостью . Построенные таким образом диаграммы называют диаграммой растяжения или условной диаграммой растяжения, так как напряжения и относительные деформации вычисляются по отношению к начальной площади поперечного сечения и длине образца. На рис. 6.4 а изображена условная диаграмма растяжения образца пластичного материала, например, углеродистой стали Ст3, а на рис.6.4 б - образца материала с ограниченной пластичностью.

С ростом деформации от нуля происходит увеличение напряжения в соответствии с законом Гука на отрезке прямой ОА. Наибольшее напряжение, при котором еще соблюдается закон Гука, называется пределом пропорциональности . Индекс pr от английского слова proportional – пропорциональный. Отрезок ОА называется зоной упругости, модуль упругости материала .

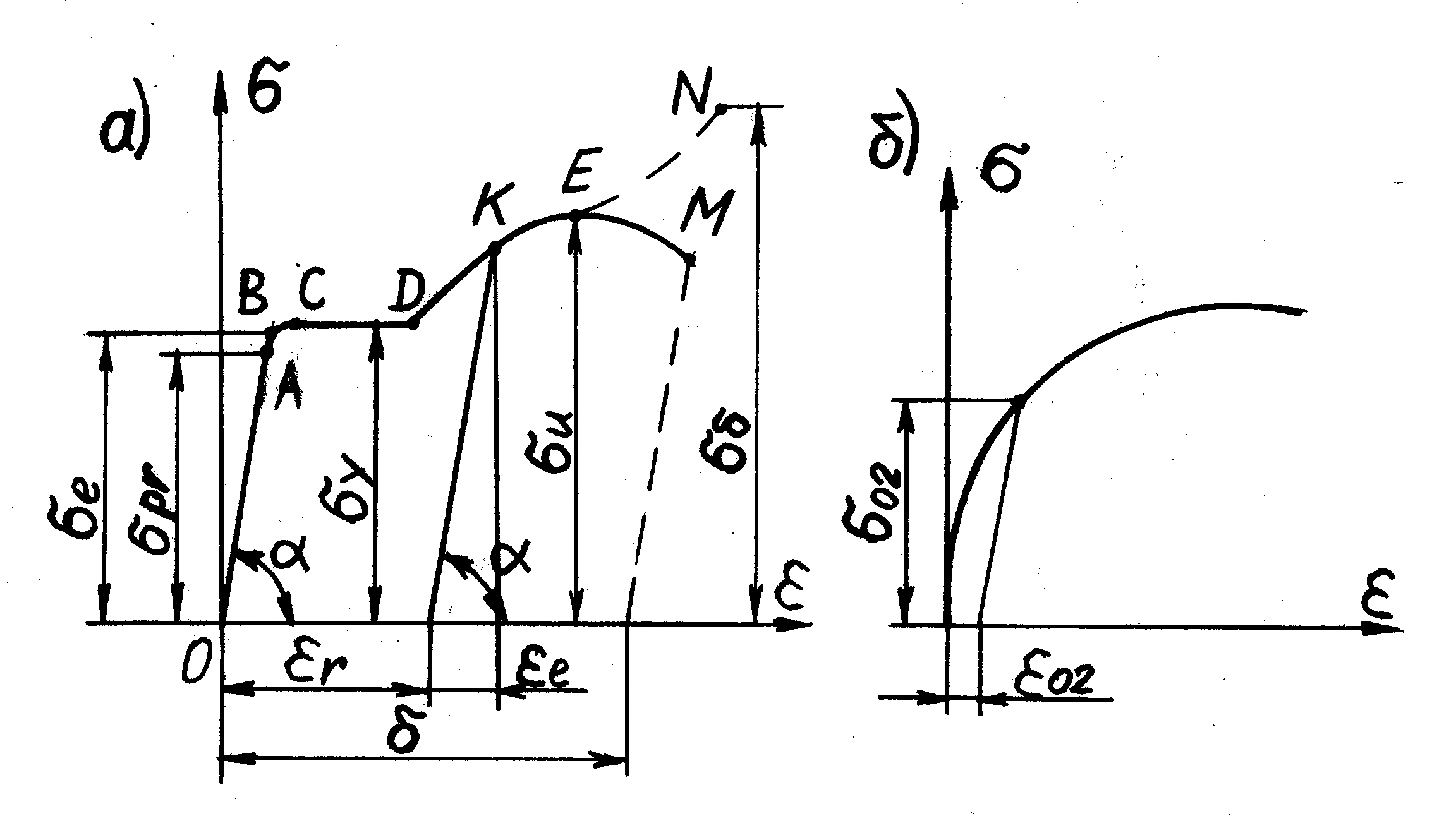
Рис. 6.4

С дальнейшим ростом деформации зависимость становится нелинейной. Точка В соответствует пределу упругости – максимальному напряжению, при котором пластические деформации в материале практически отсутствуют, т. е. их величина в зависимости от вида техники принимается или . Индекс е от английского слова elastic – упругий.

Участок СD – зона текучести диаграммы соответствует явлению текучести, когда образец деформируется практически при неизменном усилии. Наименьшее напряжение, при котором образец деформируется без увеличения растягивающего усилия, называется пределом текучести . Индекс у от английского слова yield – текучесть. В зоне текучести на полированной поверхности образцов появляются темные наклонные полосы, которые, как правило, составляют с осью образца углы, приблизительно равные 45⁰. Эти линии, носящие названия линии Людерса – Чернова, представляют собой микроскопические неровности вследствие необратимых сдвигов, происходящих в кристаллах под действием наибольших касательных напряжений. Это приводит к изменению внутренней структуры материала и его упрочнению.

Участок DE – зона упрочнения диаграммы. Здесь материал снова демонстрирует способность упрочняться, т. е. для увеличения деформации необходимо увеличивать усилие. Максимальное напряжение при испытании образца называется пределом прочности или временным сопротивлением (напряжение, соответствующее точке E). Индекс и от английского слова ultimate – предельный.

До точки E удлинение образца происходит равномерно по всей длине. Сохраняется первоначальная цилиндрическая форма, поперечные размеры изменяются равномерно и незначительно. В окрестностях точки E возникает, так называемая шейка – локальное уменьшение поперечного сечения. Участок EM диаграммы отвечает процессу неравномерного деформирования образца. Деформации образца происходят в месте образования шейки. По мере удлинения образца его сужение в области шейки прогрессирует, благодаря чему уменьшается напряжение .

Точка M диаграммы соответствует окончательному разрушению образца. Отношение разрушающей нагрузки к наименьшей площади поперечного сечения в области шейки называется напряжением разрушения , где нижний индекс обозначает относительную остаточную деформацию к моменту разрушения образца.

При построении условной диаграммы мы не учитывали изменения A₀ и l₀ в процессе испытания. Диаграмма напряжений, построенная с учетом сужения площади поперечного сечения А₀ и местного увеличения деформации называется диаграммой истинных напряжений (на рис. 6.4а показана пунктиром).

Величины принято называть механическими характеристиками кратковременной прочности материала, так как при длительном действии статических нагрузок наблюдаются явления называемые ползучестью и релаксацией. Ползучестью называется способность материала деформироваться во времени при действии постоянных нагрузок. Это явление присуще таким материалам, как полимеры, бетон, кирпич, древесина и т. п. Металлы также обнаруживают это свойство, которое становится особенно заметным при высокой температуре. Релаксацией называется процесс непрерывного во времени уменьшения напряжений за счет нарастания пластической деформации. В отечественной литературе, до недавнего времени, нижние индексы механических характеристик обозначались русскими буквами:

Если испытуемый образец нагрузить до напряжения, превосходящего предел текучести , а затем разгрузить (см. точку К на рис. 6.4), то в процессе разгрузки график зависимости между напряжением и деформацией изобразится отрезком прямой, параллельна прямой ОА первоначального нагружения. При повторном нагружении образца диаграмма растяжения практически накладывается на эту прямую и далее на кривую KEМ, как будто промежуточной разгрузки не было. Последнее означает, что модуль упругости Е при нагрузке и при разгрузке имеет одно и то же значение.

При разгрузке относительная деформация полностью не исчезает. Она уменьшается только на упругую часть полной деформации . Остаточной (пластической) деформации соответствует величина . Индексы и от английских слов elastic и rest (упругий и остаточный).

В результате этой процедуры у материала улучшились упругие свойства – повысились предел пропорциональности и предел упругости, но зато ухудшились пластические свойства – уменьшилось остаточное удлинение, т. е. материал стал более хрупким. Явление повышения упругих свойств материала в результате предварительного пластического деформирования называется наклепом. Наклеп широко используют в технике, так, например, подвергаются предварительной вытяжке цепи, канаты, арматура железобетонных конструкций и другие детали машин и механизмов.

Наклеп возникает при многих технологических процессах прокатке, штамповке, резании материалов, волочении проволоки и т. д. В некоторых случаях явление наклепа является нежелательным (например, если детали работают при переменных нагрузках). Для устранения вредного влияния наклепа материал обычно отжигают или удаляют ту часть материала, которая получила наклеп.

Для многих материалов диаграмма растяжения не имеет явно выраженной площадки текучести. В этом случае вместо предела текучести принимается так называемый условный предел текучести, равный напряжению, отвечающему остаточной деформации или 0,2% (рис. 6.4б). Условный предел текучести обозначается как .

Относительная остаточная деформация к моменту разрушения обозначается и определяется по диаграмме растяжения с помощью вычерчивания линии условной разгрузки параллельной линии ОА первоначальной нагрузке. Величина , так же как и относительное остаточное сужение к моменту разрыва

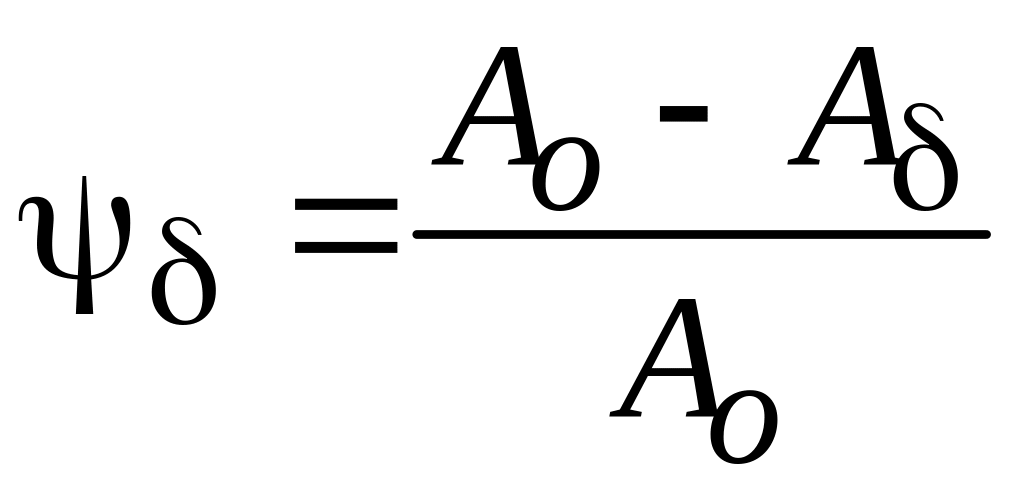, где - наименьшая площадь поперечного сечения шейки в момент разрыва, получили название механических характеристик пластичности.

Механические характеристики некоторых материалов приводятся в табл. 6.1

Таблица 6.1

Материал	Характеристика
	Е, МПа	, МПа	, МПа	, %	, %
Сталь Ст 3		240	450	26	50
Сталь 15		210	350	28	55
Сталь 45		340	610	24	45
Сталь 30ХГСА		950	1200	13	50
Чугун СЧ 15 - 32		-		0,6	-
Медь прутковая		250	320	15	45
Дуралюмин Д16		240	420	18	-

* В знаменателе указана соответствующая характеристика при сжатии.

Чем больше величины и , тем более пластичен материал. Для конструкционных сталей эти величины находятся в пределах , . Условно считается, что материал пластичен, если и и хрупким, если и . Между материалами хрупкими и пластичными можно выделить промежуточную группу – материалы ограниченной пластичности. Однако пластичность и хрупкость не могут быть отнесены только к материалу: один и тот же материал в зависимости от характера напряженного состояния, температуры и скорости деформирования, среды, в которой он находится (химические вещества, радиация), может проявлять себя как пластичный или хрупкий. В обычных условиях к высокопластичным материалам можно отнести многие технически чистые металлы: железо, алюминий, медь, никель, золото и т. д. Хорошей пластичностью обладают и многие сплавы, в том числе и низкоуглеродистые стали. К хрупким материалам относятся стекло, фарфор, керамика, кирпич, чугун, закаленная сталь и т. д.

Испытания сжатия проводят либо на кубиках, либо на коротких цилиндрических образцах с отношением высоты к диаметру, не превышающим 2, что связано с возможной потерей устойчивости более длинных образцов.

Для пластичных материалов, например углеродистой стали, диаграмма сжатия имеет вид кривой, показанной на рис. 6.5 а. Здесь, как и при растяжении, обнаруживается площадка текучести, которая, однако, менее выражена. Установлено, что для пластичных материалов значения пределов текучести при растяжении и сжатии практически равны.

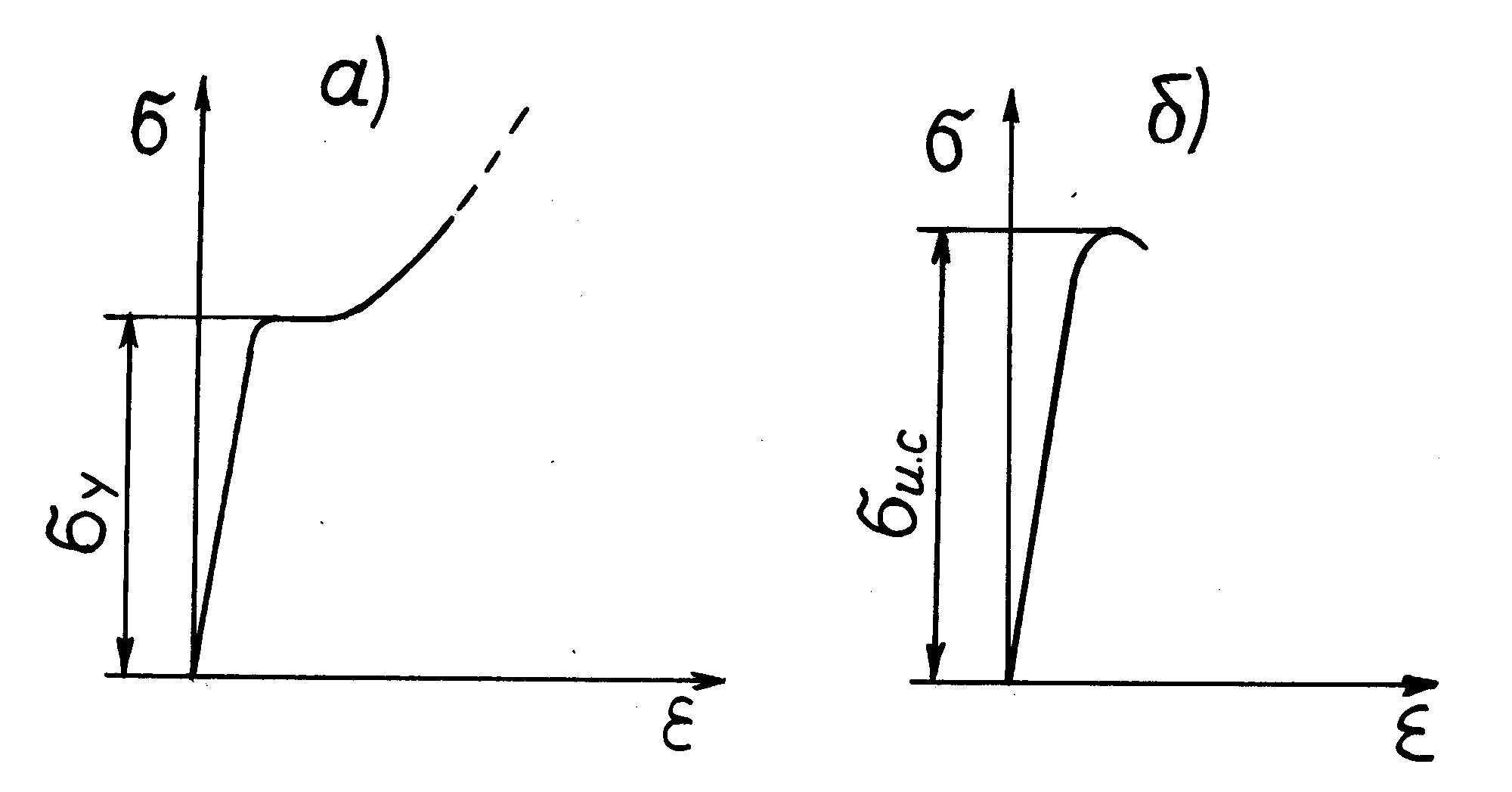
Рис. 6.5

В отличие от диаграммы растяжения здесь нет спадающей ветви диаграммы. Происходит это потому, что площадь поперечного сечения сжатого образца все время увеличивается. Образцы высоко пластичных материалов осаживаются «в лепешку», практически не разрушаясь.

Диаграмма сжатия хрупких образцов представлена на рис.6.5 б . Как показывают эксперименты предел прочности при сжатии в несколько раз (в 3 – 5 раз) превосходит предел прочности при растяжении . Индексы с и t от английских слов compression, tension – сжатие и растяжение. С русскими индексами предел прочности при сжатии - , предел прочности при растяжении .

Образцы хрупких материалов разрушаются на множество фрагментов. Разрушению предшествует появление множества трещин. Часть исследователей считает направление трещин как случайное, другая часть исследователей считают наиболее вероятной ориентацией трещин под некоторым углом к направлению сжимающей силы.

Кроме испытания образцов на растяжение и сжатие, существует более оперативный метод испытаний – оценка прочности стали по ее твердости. Под твердостью материала понимается его способность противодействовать механическому проникновению в него другого, более твердого тела.

Наиболее широкое применение получили пробы на твердость по Бринеллю и по Роквелу. В первом случае в поверхность исследуемой детали вдавливается стальной шарик диаметром 10 мм под нагрузкой 20 кН , во втором – алмазный конус. Твердость по Бринеллю принято обозначать НВ (число твердости по Бринелю равно отношению нагрузки к площади сферической поверхности отпечатка), а по Роквелу – HRC. Последний способ применяют в основном для закаленных сталей, где способ по Бринеллю дает значительные погрешности.

Экспериментально установлено, что число твердости стали и ее предел прочности связаны соотношением . В справочной литературе приводятся таблицы перевода твердости HRC в числа твердости НВ.