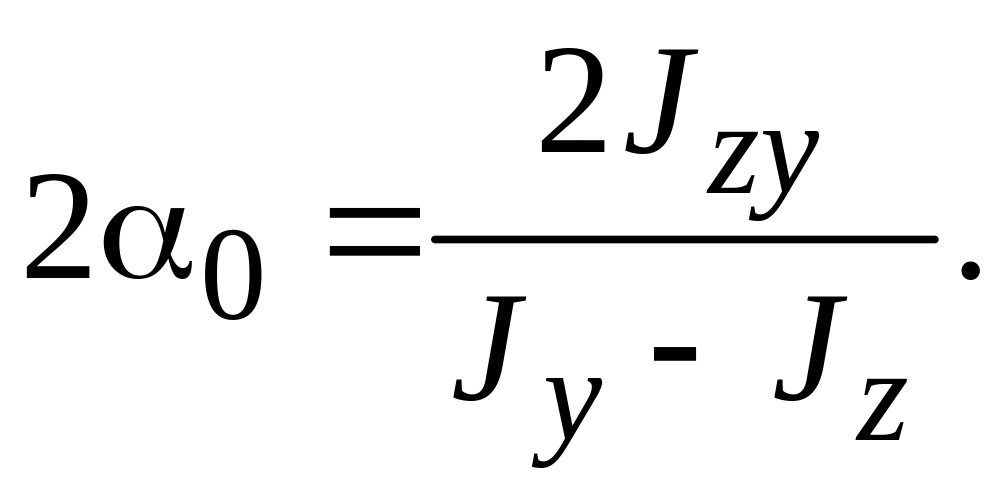- •Лекция № 1 основные понятия и исходные положения
- •1.1. Общие сведения
- •1.2. Схематизация элементов конструкции
- •1.3. Внешние силовые воздействия (нагрузки)
- •1.4. Основные гипотезы
- •1.5. Опоры и связи
- •Лекция № 2 внутренние усилия, построение эпюр
- •2.1. Внутренние силы. Метод сечений
- •2.2. Внутренние усилия при растяжении и сжатии
- •2.3. Внутренние усилия при кручении
- •2.4. Внутренние усилия при изгибе
- •Лекция № 3 геометрические характеристики плоских сечений
- •3.1. Основные понятия
- •3.2. Площадь поперечного сечения
- •3.3. Статический момент сечения
- •3.4. Осевой (экваториальный) момент инерции
- •3.5. Полярный момент инерции
- •3.6. Центробежный момент инерции
- •3.7. Изменение моментов инерции при повороте осей
- •Лекция № 4 теория напряженного состояния
- •4.1. Напряжения. Связь между напряжениями и внутренними силовыми факторами
- •4.2. Напряженное состояние
- •4.3. Линейное напряженное состояние. Закон Гука
- •4.4. Плоское напряженное состояние
- •4.5. Обобщенный закон Гука
- •4.6. Изменение объёма материала при объёмном напряженном состоянии
- •4.7. Потенциальная энергия при объёмном напряженном состоянии
- •Лекция № 5 теория деформированного состояния
- •5.1 Деформированное состояние в точке
- •5.2. Основные понятия и определения
- •5.3. Зависимость между деформациями и перемещениями. Формулы Коши.
- •5.4. Экспериментальное определение деформаций и напряжений методом тензометрии
- •Лекция №6 растяжение и сжатие
- •6.1. Напряжения и деформации при растяжении – сжатии.
- •6.2. Потенциальная энергия упругой деформации при растяжении и сжатии
- •6.3. Механические испытания образцов материалов на растяжение и сжатие.
- •6.4. Предельное состояние. Расчеты на прочность и жесткость
- •6.5. Термические напряжения и деформации
- •Лекция № 7 расчет гибких нитей (проводов)
- •7.1. Гибкая нить под действием распределенной нагрузки
- •7.2. Расчет симметричных гибких нитей
- •Лекция № 8 плоский изгиб, расчет на прочность
- •8.1. Основные понятия
- •8.2. Прямой чистый изгиб
- •8.3. Составные балки из различных материалов
- •8.4. Прямой поперечный изгиб
- •Лекция № 9 перемещения при изгибе, расчет на жесткость
- •9.1. Основные понятия
- •9.2. Дифференциальное уравнение изогнутой оси балки
- •Метод непосредственного интегрирования дифференциального уравнения изогнутой оси балки. Метод начальных параметров
- •Расчеты на жесткость при изгибе
- •Лекция № 10 сдвиг и кручение
- •10.1. Чистый сдвиг
- •10.2 Расчет на срез
- •Расчет на смятие
- •10. 4. Кручение
- •10.5. Расчет на прочность и жесткость при кручении
- •10.6. Кручение стержней с некруглым поперечным сечением
- •Лекция № 11 сложное сопротивление
- •11.1. Общие понятия
- •11.2 Косой изгиб
- •11.3. Изгиб балки при действии продольных и поперечных сил
- •11.4. Внецентренное сжатие или растяжение
- •11.5. Совместное действие изгиба и кручения
- •Лекция № 12 гипотезы (теории) прочности. Расчет по допускаемым нагрузкам
- •12.1. Основные положения
- •12.2. Третья теория прочности
- •12.3. Четвертая теория прочности
- •12.4. Теория прочности Мора
- •12.5. Расчет элементов конструкций по методу допускаемых нагрузок
- •Лекция № 13 усталость материалов при циклических нагрузках
- •13.1. Основные понятия
- •13.2. Основные характеристики цикла и предел усталости
- •13.3. Расчет на усталостную прочность
- •Лекция № 14 энергетические способы определения пермещений
- •14.1. Теорема Клайперона.
- •14.2. Потенциальная энергия в общем случае нагружения бруса
- •14.3.Теорема Кастильяно
- •14.4. Интеграл Максвелла – Мора
- •14.5. Способ Верещагина
- •Библиографический список
- •Васильев Владислав Васильевич
4.5. Обобщенный закон Гука
При
растяжении элементарного параллелепипеда
его продольное ребро
увеличивается на величину
![]() ,
а поперечные ребра
,
а поперечные ребра
![]() и
и
![]() соответственно уменьшаются на величину
соответственно уменьшаются на величину
![]() и
и
![]() .
Величины
и
− абсолютные
поперечные деформации ребер.
.
Величины
и
− абсолютные
поперечные деформации ребер.
Отношение абсолютной поперечной деформации ребра к его первоначальному размеру называется относительной поперечной деформацией:
![]() ;
;
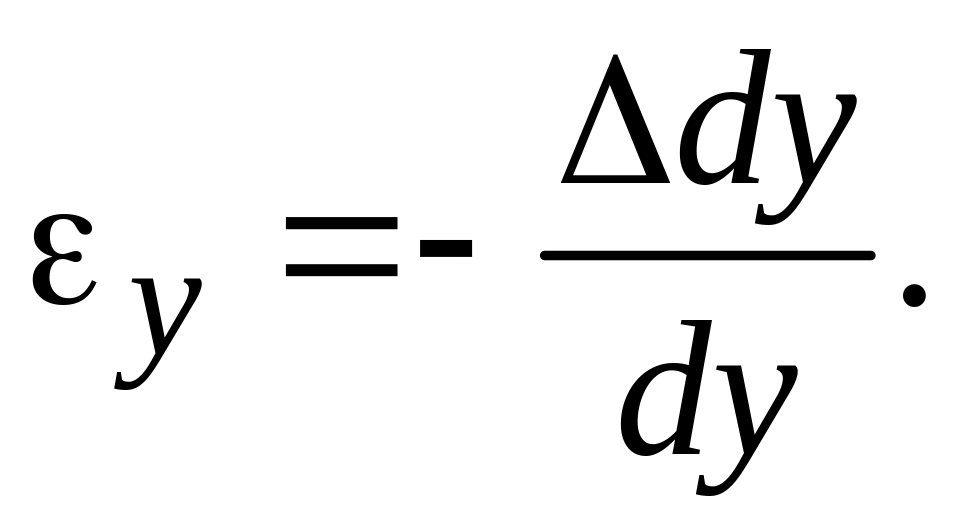
Экспериментально установлено, что для изотропных материалов поперечные деформации равны между собой и связаны линейным соотношением с продольной деформацией:
εпопер![]() ;
εпопер.
;
εпопер.
![]() ,
(4.16)
,
(4.16)
где
![]() - коэффициент пропорциональности,
называемый коэффициентом Пуассона,
- коэффициент пропорциональности,
называемый коэффициентом Пуассона,
![]() 0,5.
0,5.
Коэффициент
Пуассона,
так же как и модуль упругости, является
механической
константой материала.
Ориентировочные значения коэффициента
Пуассона для некоторых конструкционных
материалов: сталь и алюминиевые сплавы
−
![]() ,
медь и ее сплавы −
,
медь и ее сплавы −
![]() ,
резина −
,
резина −
![]() ,
пробка −
,
пробка −
![]() .
.
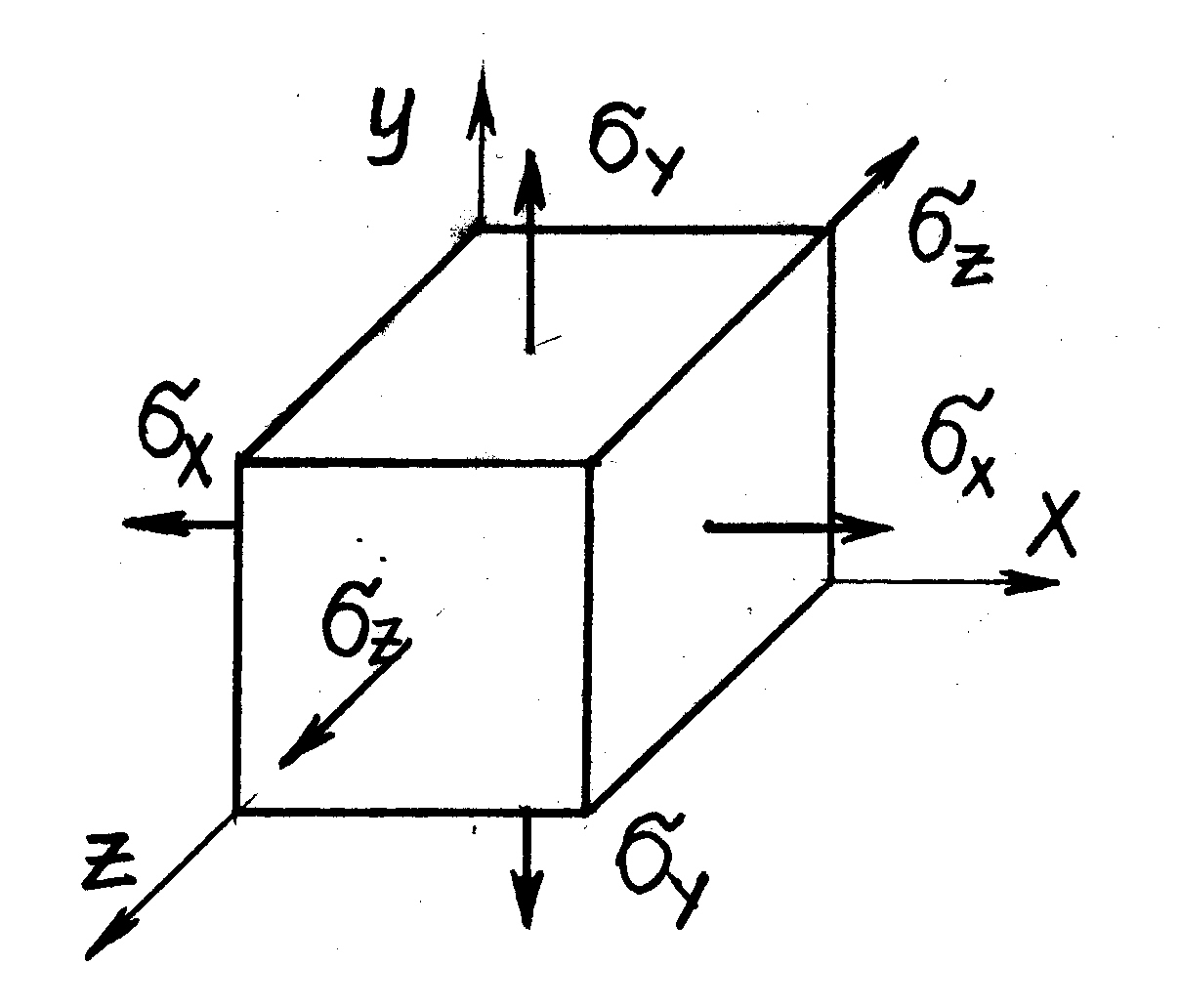
В случае объёмного напряженного состояния на гранях выделенного элемента возникают нормальные и касательные напряжения (рис. 4.6).
Рис. 4.6 |
Касательные напряжения, вызывая деформации сдвига, не изменяют длины ребер элемента, поэтому на рис. 4.6 они условно не показаны. В случае идеально упругого и изотропного материала линейные и угловые деформации можно рассматривать как независимые. Воспользуемся принципом независимости действия сил (принцип суперпозиции) и рассмотрим линейные деформа- |
ции в направлении оси х, обусловленные нормальными напряжениями.
От
действия только напряжений
![]() деформация в направлении оси х
равна
деформация в направлении оси х
равна
![]()
От
действия только напряжений
![]() или
или
![]() деформации в направлении оси х
соответственно равны
деформации в направлении оси х
соответственно равны
 ;
;
![]() .
.
Знак минус указывает, что в направлении оси х эти напряжения уменьшают размеры элемента.
Складывая все деформации в направлении оси х, получим
 .
.
Рассуждая
аналогично, можно получить выражения
для линейных деформаций в направлении
осей
![]() и
и
![]() ,
т. е.
,
т. е.
![]() и
и
![]() .
Следовательно,
.
Следовательно,
![]()
![]() (4.17)
(4.17)
![]()
Полученные зависимости являются аналитическим выражением обобщенного закона Гука. В эти формулы растягивающие напряжения подставляются со знаком плюс, а сжимающие – со знаком минус.
Полезно для запоминания обратить внимание (табл. 4.1) на полную аналогию структурных формул для напряжений (нормальных и касательных) при плоском напряженном состоянии и моментов инерции плоских сечений.
Таблица 4.1
Напряжения |
Моменты инерции |
|
|
|
|
На главных площадках
|
Относительно главных осей
|
|
|
4.6. Изменение объёма материала при объёмном напряженном состоянии
Мысленно
выделим из твердого тела параллелепипед
со сторонами а,
в, с
и пусть сторону параллелепипеда а
деформирует главное напряжение
![]() ,
сторону в
-
,
сторону в
-
![]() и сторону с
-
и сторону с
-
![]() .
Первоначальный объем параллелепипеда
до деформации
.
Первоначальный объем параллелепипеда
до деформации
![]() .
.
Под действием главных напряжений стороны изменят свою длину:
![]()
Очевидно, что:
![]()
Объём параллелепипеда после деформации
![]() ,
пренебрегая произведениями деформаций,
как величинами второго порядка малости,
окончательно получим
,
пренебрегая произведениями деформаций,
как величинами второго порядка малости,
окончательно получим
![]() .
.
Относительное изменение объёма параллелепипеда
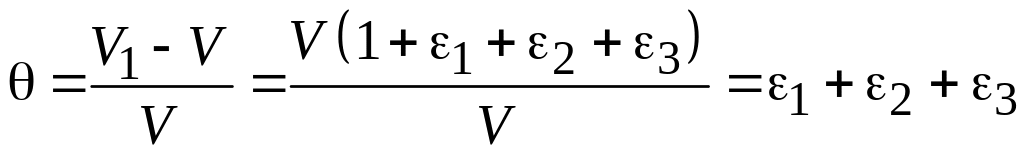 .
(4.17)
.
(4.17)
С учетом обобщенного закона Гука имеем
![]() .
(4.18)
.
(4.18)
Учитывая инвариантность суммы нормальных напряжений можно записать
![]() (4.19)
(4.19)
Обозначим
 и перепишем формулу (4.18)
и перепишем формулу (4.18)
 (4.20)
(4.20)
где
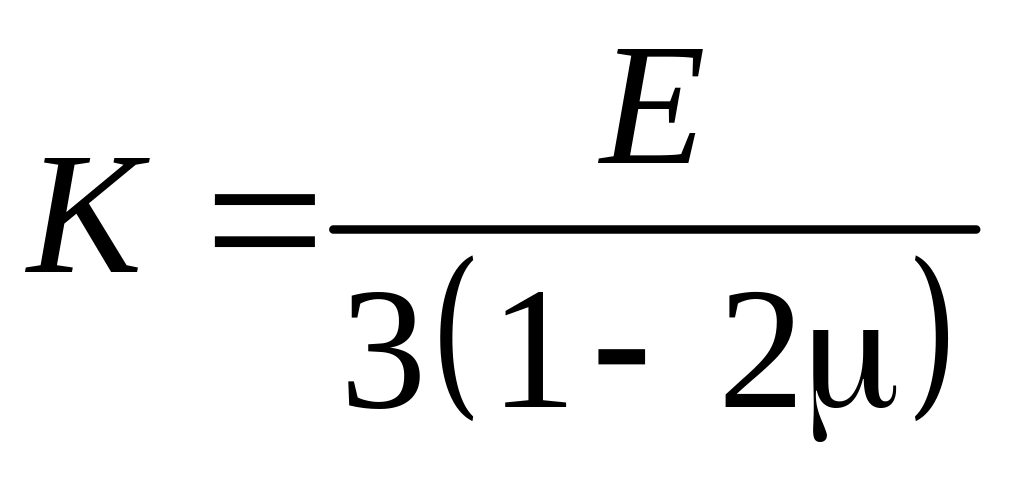 - объёмный модуль упругости.
- объёмный модуль упругости.
Рассмотрим
случай всестороннего гидростатического
сжатия материала, когда
![]() .
По формуле (4.20) имеем
.
По формуле (4.20) имеем
![]()
Из последней формулы следует, что коэффициент Пуассона не может быть больше 0,5, так как в противном случае при всестороннем сжатии тело не уменьшается, а увеличивается в объёме. Этот вывод подтверждается опытными данными. В природе не обнаружены материалы, у которых коэффициент Пуассона был бы больше 0,5. Есть материалы (например, натуральный каучук, парафин), у которых коэффициент Пуассона приближается к 0,5. В этом случае при всестороннем сжатии не происходит изменение объёма материала и такие материалы по своим упругим свойствам приближаются к несжимаемым жидкостям.





 .
.