3.7. Изменение моментов инерции при повороте осей

Пусть моменты инерции относительно осей y и z известны. Определим их моменты инерции относительно осей u и v, повернутых на угол α против хода часовой стрелки.

Из рис. 3.5 очевидно, что координаты элементарной площадки в системе координат u и v

(3.16)

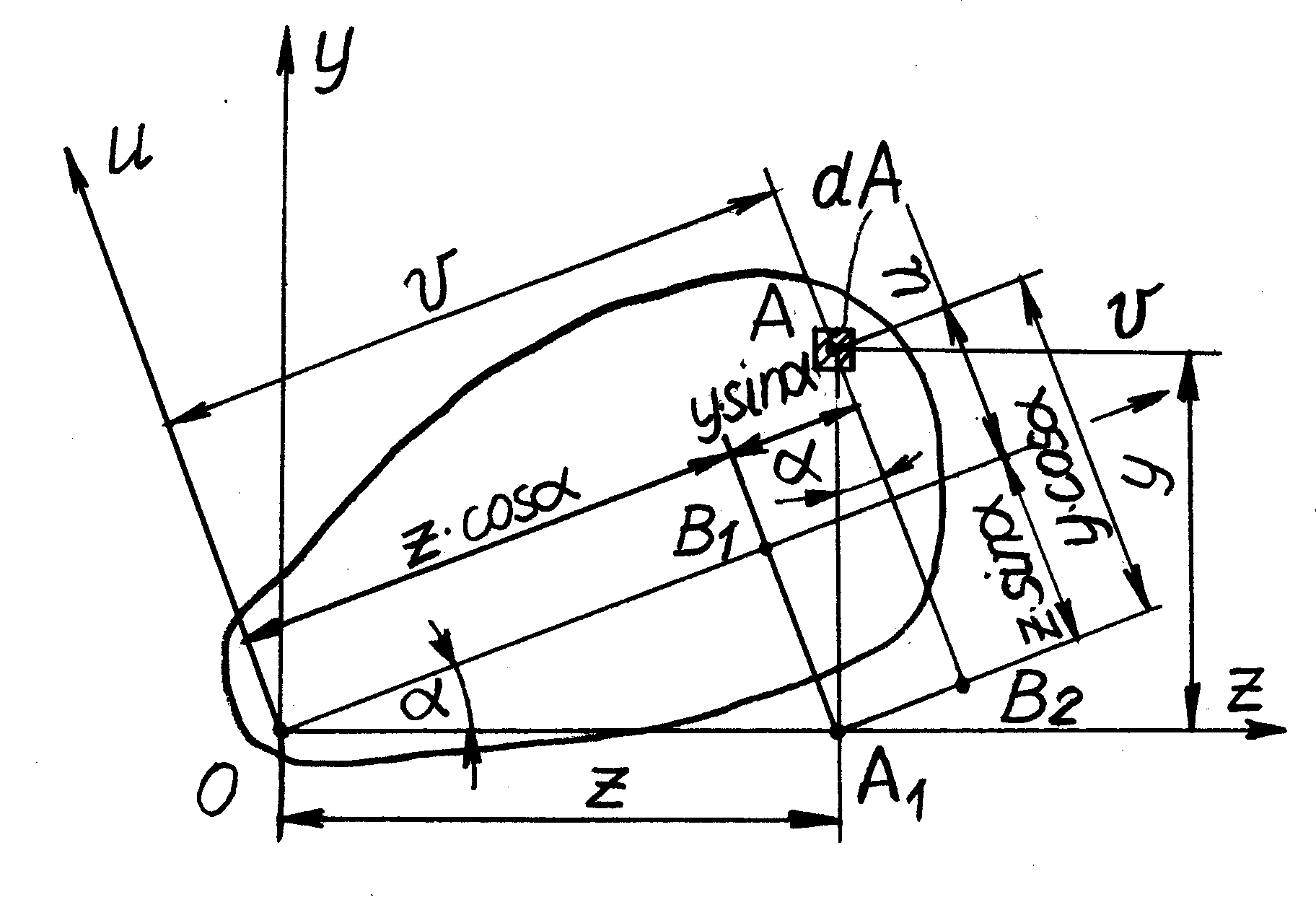
Рис. 3.5

Найдем осевые моменты инерции относительно оси u и v:

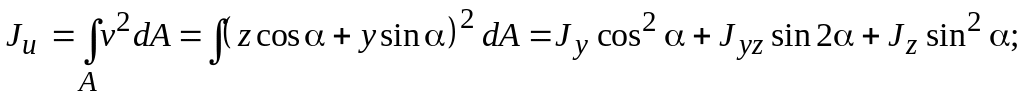(3.17)

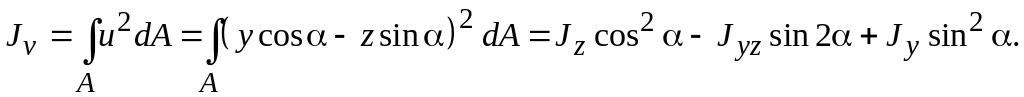(3.18)

При сложении уравнений (3.17) и (3.18) получим подтверждение ранее сделанного вывода, что сумма осевых моментов при повороте прямоугольных осей есть величина постоянная:

(3.19)

Центробежный момент инерции относительно повернутых осей

(3.20)

Для нахождения экстремальных значений осевых моментов возьмем их первые производные и приравняем нулю:

;

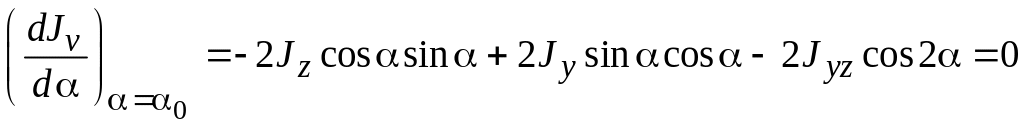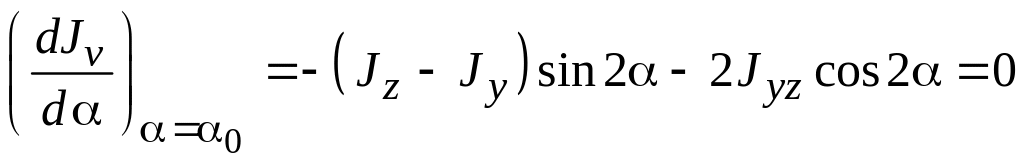(3.21)

Сравнивая уравнение (4.21) с уравнением (4.20) можно записать

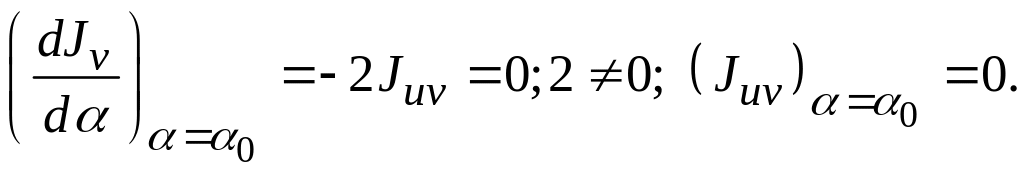(3.22)

Следовательно, относительно главных осей центробежный момент равен нулю, а осевые моменты принимают экстремальные значения.

Решая уравнение (3.21) относительно , получим

(3.23)

Одному и тому же значению соответствуют углы и или и . Относительно одной из этих осей осевой момент будет максимальным, относительно другой – минимальным.

Формула (3.23) не дает понимания, в какую сторону надо повернуть координатные оси и относительно которой из осей осевой момент будет максимальным (минимальным). При выборе главных осей инерции следует руководствоваться следующим правилом:

− если центробежный момент инерции величина отрицательная , то главная ось, относительно которой осевой момент инерции будет иметь максимальное значение, проходит через нечетные квадранты (I и III);

− ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение.

Главные моменты инерции определяются по следующим формулам:

(3.24)

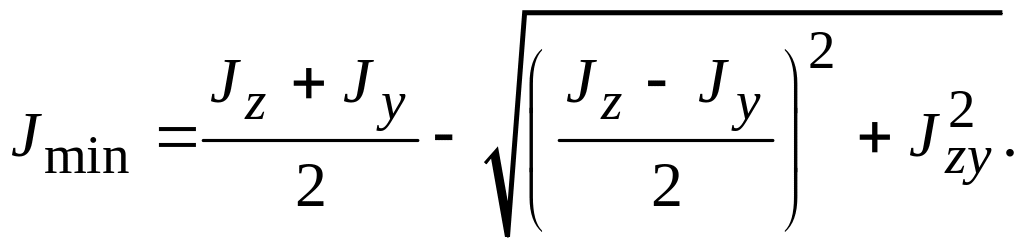(3.25)

Вопросы для самопроверки

1. Приведите определение статического момента плоского сечения.

2. Дайте определение осевых и центробежных моментов инерции плоского сечения.

3. Как связаны между собой осевые и полярные моменты инерции?

4. Запишите формулы для вычисления моментов инерции прямоугольника и круга.

5. Приведите формулы моментов инерции сечения относительно параллельных осей.

6. Запишите формулы преобразования моментов инерции при повороте осей.

7. Какие оси называются главными осями инерции сечения?

8. Как определить направление главных осей инерции?

9. Запишите формулы для вычисления главных моментов инерции сечения.

Лекция № 4 теория напряженного состояния

4.1. Напряжения. Связь между напряжениями и внутренними силовыми факторами

Напряжения характеризуют интенсивность внутренних сил, действующих на данную площадку в рассматриваемой точке. Напряжения, в общем случае, не только различны в различных точках рассматриваемого элемента конструкции, но различны в одной и той же точке по различно наклоненным площадкам. Понятие напряжения является фундаментальным для всей механики твердого деформируемого тела. Это понятие сформулировал и ввел в научную литературу в 1822 г. французский ученый Огюстен Луи Коши. Прочность материала в окрестностях данной точке определяется именно величиной напряжений.

Рассмотрим тело, находящееся в равновесии под действием внешней нагрузки (рис. 4.1). Рассечем тело, и выделим малую площадку , относительно точки K. Ориентация площадки в пространстве определяется нормалью площадки n. Обозначим равнодействующую внутренних сил, действующих на этой площадке, , тогда отношение представляет собой среднее напряжение на площадке.

Для того чтобы определить напряжения в точке K будем стягивать площадку к точке. Тогда отношение

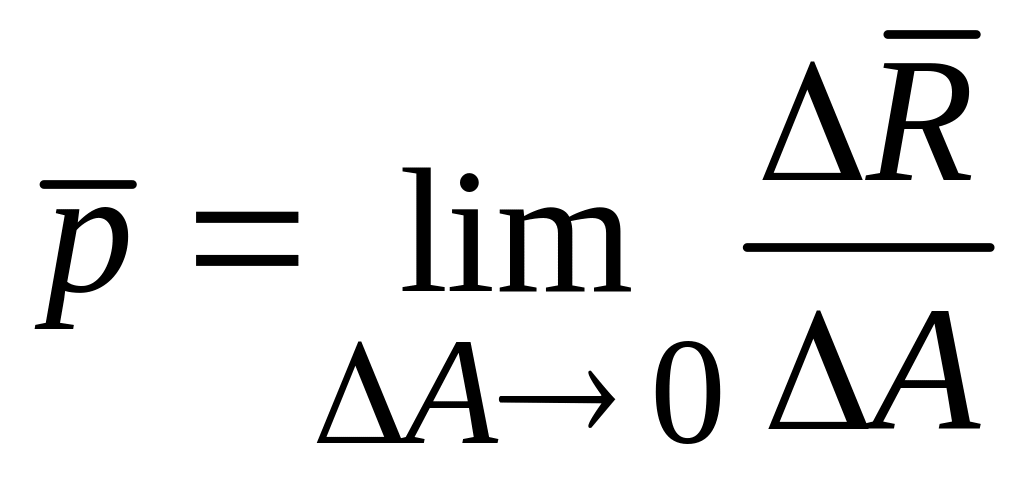(4.1)

будет полным напряжением от внутренних сил, передающихся в точке через выделенную площадку. Размерность напряжения: Па = Н/м².

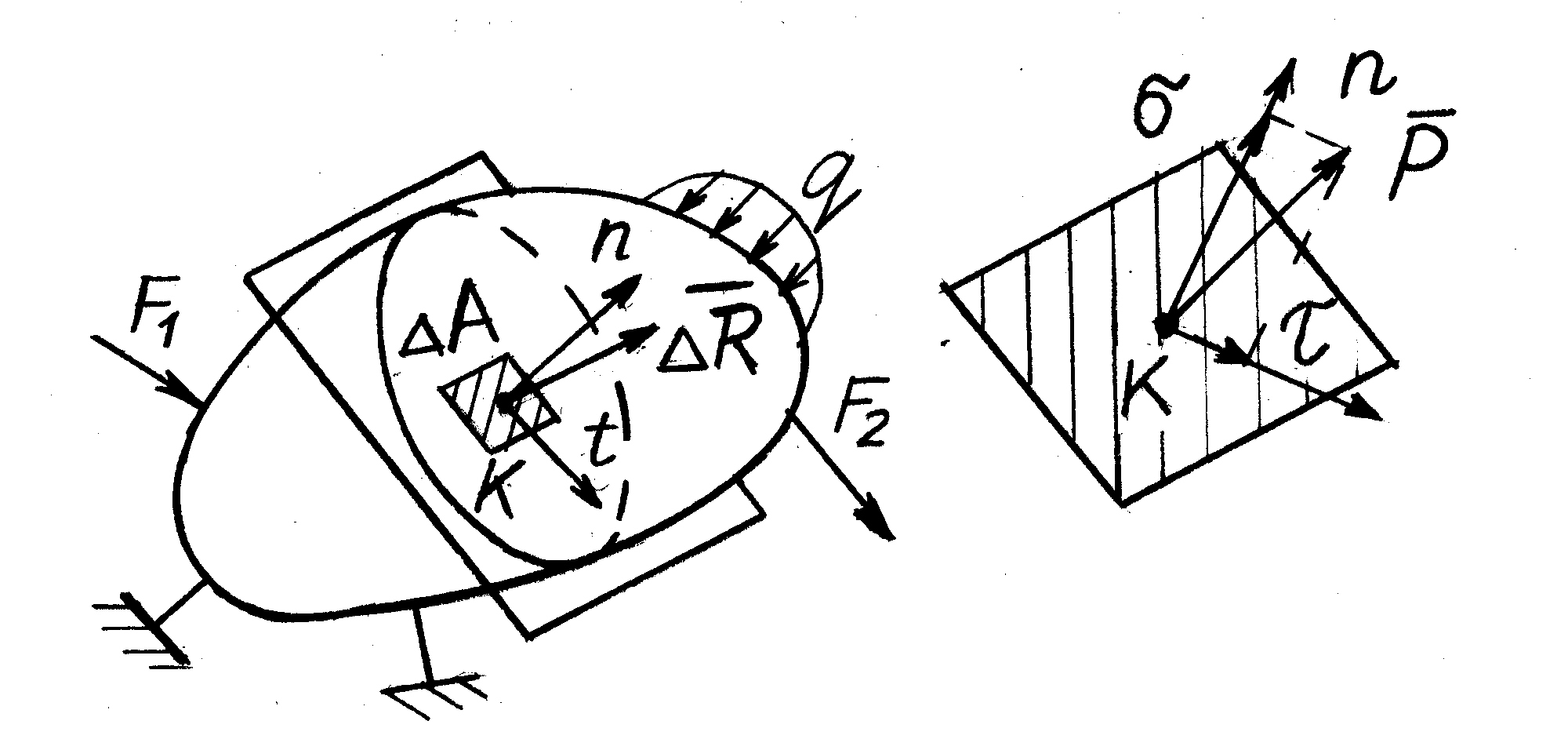
Рис. 4.1

Полное напряжение раскладывается на составляющие: нормальное напряжение (проекция полного напряжения на нормаль к площадке) σ и касательное напряжение (проекция полного напряжения на плоскость площадки) τ. При этом . Обычно принято рассматривать площадки, перпендикулярные к продольной оси х бруса, тогда координатные оси y и z будут лежать в плоскости площадки. В этом случае касательные напряжения можно разложить на составляющие по этим осям:

и .

В общем случае напряженного состояния, если в окрестностях рассматриваемой точки выделить элементарный параллелепипед со сторонами dx, dy и dz, то на его гранях будут действовать нормальные и касательные напряжения (рис. 4.2).

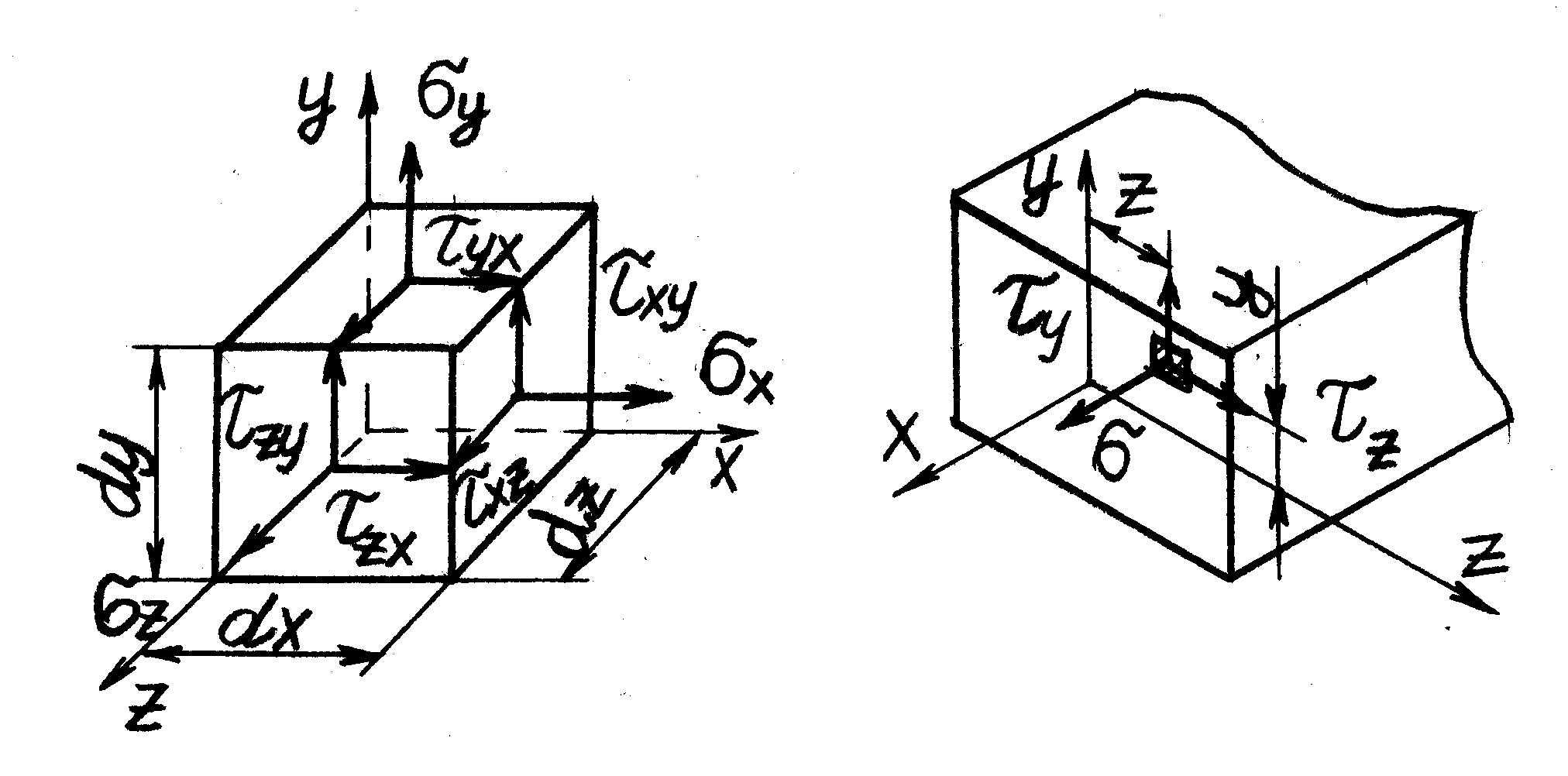
Рис. 4.2

Индексы x, y и z нормальных напряжений соответствуют осям, которые являются нормалями к соответствующим граням параллелепипеда. Первые индексы касательных напряжений соответствуют осям, которые являются нормалями к соответствующим площадкам, вторые – соответствуют осям, параллельно которым направлены касательные напряжения.

Положительные нормальные напряжения стремятся оторвать частицы друг от друга, и направлены в сторону внешней нормали. Касательные напряжения стремятся сдвинуть частицы относительно друг друга. Касательные напряжения считаются положительными, если на площадке с внешней нормалью они действуют по положительным направлениям координатных осей. На рис. 4.2 все напряжения положительные.

Внутренние усилия можно выразить через напряжения, предполагая их известными в каждой точке (рис. 4.2). Элементарные силы на площадке dA в рассматриваемой точке будут , , . Проецируя все элементарные силы на оси x, y и z и суммируя силы и моменты этих сил относительно координатных осей по всему сечению, получим

; ; ; (4.2)

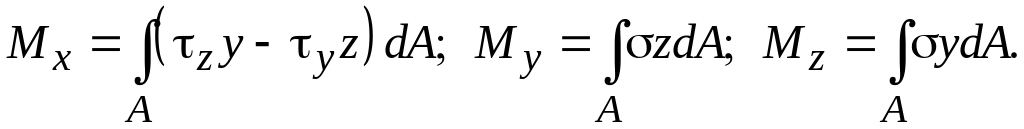(4.3)

Эти уравнения определяют физическую сущность внутренних силовых факторов, но не позволяют определять сами силовые факторы. Наоборот, с помощью метода сечений определяются внутренние силовые факторы, а на основе этих интегральных зависимостей и с привлечением дополнительных гипотез определяются напряжения.