4.16.4. Парабола

Определение.Параболой называется множество всех точек плоскости, каждая из которых равноудалена от данной точки, называемой фокусом F, и данной прямой l, называемой директрисой.

Если расстояние от фокуса F до директрисы l обозначить через p, расположить фокус F на оси Ox, которая перпендикулярна директрисе l, а ось Oy – посередине между фокусом и директрисой параллельно последней, то парабола задастся уравнением

которое называется каноническим уравнением параболы (рис. 4.23).

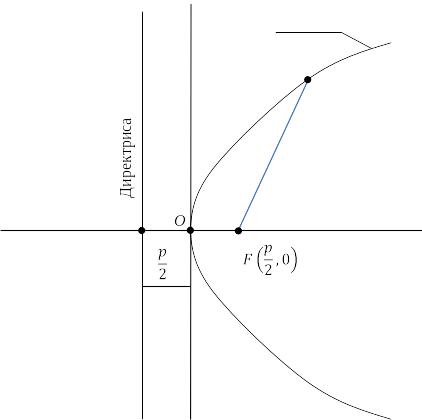
Рис. 4.23

Число p, равное расстоянию от фокуса F до директрисы l, называется параметром параболы, точка – ее вершиной, а ось Ox – осью симметрии параболы. Уравнение директрисы l имеет вид: . Эксцентриситет  параболы по определению считается равным 1: .

Замечания. 1) Уравнение также задает параболу, симметричную относительно оси Ox (рис. 4.24). Фокус F имеет координаты , а уравнение директрисы: .

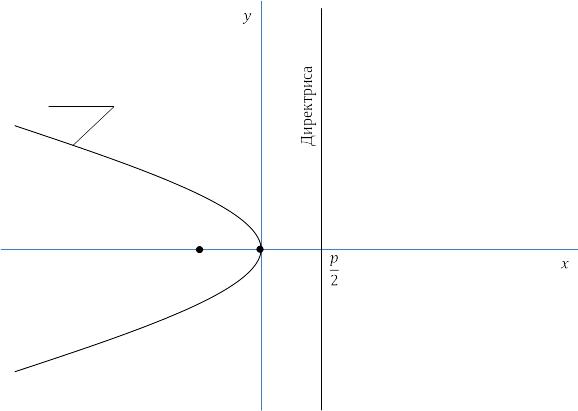
Рис. 4.24

2) Уравнения также задают параболы, но сим-метричные относительно оси Oy. У параболы фокус , уравнение директрисы (рис. 4. 25). Для параболы фокус , а уравнение директрисы (рис. 4. 26).

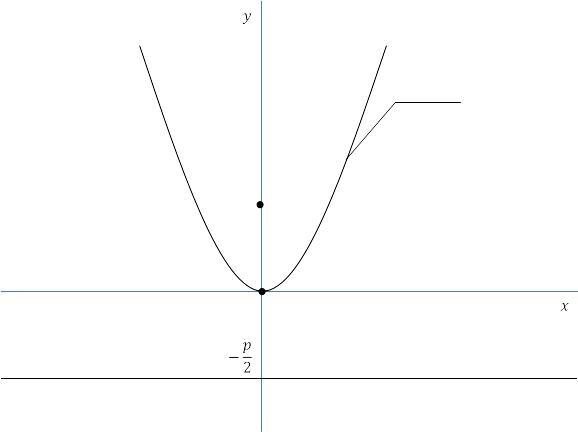
Рис. 4.25

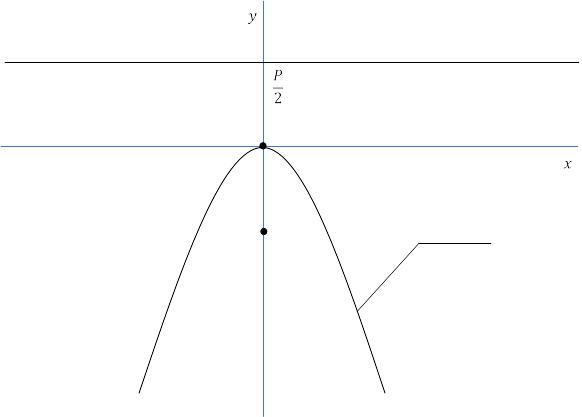
Рис. 4.26

3) Уравнения парабол с осями симметрии, параллельными координатным осям, имеют вид:

.

Известно, что для любой линии второго порядка на плоскости существует прямоугольная декартова система координат, в которой эта линия задается каноническим уравнением.

Покажем на конкретных примерах, как практически привести уравнение линии 2-го порядка, не содержащее члена с произведением переменных, т. е. в (4.77), к каноническому виду.

П ример 4.52. Линия второго порядка задана уравнением

Определить вид этой линии и нарисовать ее.

Решение. Уравнение (4.90) не является каноническим. Выделим полный квадрат, включающий в себя все слагаемые с переменной y, причем коэффициент при y² обязательно выносим за скобки.

Применив преобразование параллельного переноса , из последнего уравнения получаем каноническое уравнение . Отсюда видим, что рассматриваемая линия – парабола, симметричная относительно оси O₁X.

Ч тобы нарисовать эту линию, изобразим на одном рисунке обе системы координат Oxy и O₁XY. При параллельном переносе координатные оси перемещаются параллельно самим себе, поэтому для определения их расположения достаточно определить положение нового начала координат. В точке O₁ X = 0 и Y = 0, значит, . Через точку проводим оси, сонаправленные осям Ox и Oy, и получаем новую систему координат. В этой системе рисуем параболу , вершина которой находится в начале координат, а ветви направлены в сторону положительного направления оси O₁X симметрично этой оси (рис. 4.27).

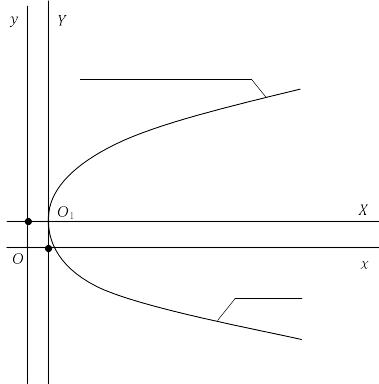
Рис. 4.27

П ример 4.53. Упростить уравнение , пользуясь переносом начала координат. Построить линию, определяемую этим уравнением.

Решение. Выделим полные квадраты по переменным x и y соответственно.

О бозначая х – 3 = X, y + 1 = Y, получим каноническое уравнение эллипса Начало новой системы координат – точка О₁(3, –1); оси О₁X, О₁Y параллельны осям Оx и Оy соответственно. Большая полуось эллипса , малая полуось Изобразим кривую на рис. 4.28.

Рис. 4.28

Пример 4.54. Составить уравнение окружности, имеющей центр в точке и радиус, равный 4.

Р ешение. Подставим значения координат центра и радиуса в уравнение (4.78), получим .

П ример 4.55. Дано уравнение эллипса . Найти: 1) длины его полуосей; 2) координаты фокусов; 3) эксцентриситет.

Решение. Приведем уравнение эллипса к каноническому виду (4.80), разделив обе части равенства на 1176: , из которого вытекают следующие соотношения:

1. , т. е. – большая полуось; – малая полуось.

2. Используя равенство (4.81), найдем . Значит, .

3. П о формуле (4.82) .

П ример 4.56. Составить уравнение эллипса, проходящего через точки .

Решение. Уравнение эллипса ищем в виде (4.80): . Так как эллипс проходит через точки , то их координаты удовлетворяют уравнению эллипса:

У множая второе равенство на (–4) и складывая с первым, находим: , т. е. . Подставляя полученное значение во второе равенство, получаем , откуда . Искомое уравнение эллипса имеет следующий вид: .

П ример 4.57. Дано уравнение гиперболы . Най-ти: 1) длины полуосей гиперболы; 2) координаты фокусов; 3) эксцент-риситет; 4) уравнения асимптот.

Решение. Разделим обе части уравнения на 144, тем самым приведя его к каноническому виду (4.84): .

1) Из последнего уравнения , т. е. – действительная полуось, – мнимая полуось.

2) Используя равенство (4.85): , получим: , а . Значит, .

3) По формуле (4.86) .

4 ) Уравнения асимптот имеют вид: . В нашем случае .

П ример 4.58. Составить каноническое уравнение гиперболы, если ее фокусы лежат на оси Oy и расстояние между ними равно 10, а длина действительной оси равна 8.

Р ешение. Искомое уравнение имеет вид (4.87): . Согласно условию . Значит, . Из (4.85) . Найдем мнимую полуось a: , т. е. . Искомое уравнение гиперболы: .

П ример 4.59. Дана парабола . Найти: 1) координаты фокуса; 2) уравнение директрисы.

Р ешение. Парабола задана каноническим уравнением . Следовательно, . Откуда получаем: 1) ; 2) – уравнение директрисы.

Пример 4.60. Составить уравнение параболы, если ее вершина совпадает с началом координат, а фокус находится в точке .

Р ешение. Так как фокус параболы находится всегда на ее оси симметрии, то в нашем случае осью параболы будет ось Ox, причем . Отсюда , значит, . При этом каноническим уравнением параболы будет , т. е. в данном случае . Отметим, что уравнение директрисы , т. е. .