4.10. Смешанное произведение векторов

Определение. Смешанным произведением трех векторов называется число, получаемое следующим образом: векторное произведение умножается скалярно на вектор Смешанное произведение векторов обозначается ( ). Таким образом, .

Смешанное произведение векторов обладает следующими свой-ствами:

1) ;

2)  , т. е. смешанное произведение не меняется при циклической перестановке векторов и меняет знак на противоположный при перемене мест любых двух рядом стоящих векторов – сомножителей;

3)  ;

4)  ;

5) модуль смешанного произведения равен объему параллелепипеда, построенного на векторах :

.

6) равенство является необходимым и достаточным условием компланарности векторов .

Если , то – правая тройка; если – левая тройка.

Если векторы заданы в ортонормированном базисе координатами , то

.

Пример 4.29. Вычислить объем треугольной пирамиды с вер-шинами А(0, 0, 1), В(2, 3, 5), С(6, 2, 3), D(3, 7, 2).

Решение. Рассмотрим три вектора (рис. 4.14):

.

Можно показать, что объем пирамиды АВСD равен шестой части объема параллелепипеда, построенного на векторах

Рис. 4.14

Тогда , а т. к.

то

Ответ: 20.

П ример 4.30. Доказать, что четыре точки А₁(3, 5, 1), А₂(2, 4, 7), А₃(1, 5, 3), А₄(4, 4, 5) лежат в одной плоскости.

Решение. Достаточно показать, что три вектора , имеющие начало в одной из данных точек, лежат в одной плоскости (т. е. компланарны). Находим координаты векторов :

Проверяем условие компланарности векторов (свойство 6 смешанного произведения):

.

С ледовательно, векторы компланарны, а значит, точки А₁, А₂, А₃, А₄ лежат в одной плоскости.

П ример 4.31. Образуют ли векторы , базис в трехмерном пространстве? Если да, то опреде-лите, какой тройкой является тройка векторов – правой или левой.

Решение. Вычислим смешанное произведение векторов :

.

Т ак как , то векторы не компланарны, а значит, образуют базис в пространстве. Учитывая, что , то тройка векторов – левая.

4.11. Полярная система координат. Уравнение линии на плоскости

4.11.1. Полярная система координат

Полярная система координат задается точкой О, называемой полюсом, лучом Оp, называемым полярной осью, и единичным вектором того же направления, что и луч Оp.

Положение точки М на плоскости определяется двумя числами: ее расстоянием r от полюса О и углом , образованным отрезком ОМ с полярной осью (рис. 4.15) и отсчитываемым в положительном направлении.

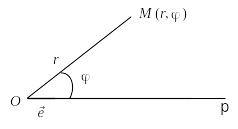
Рис. 4.15

Определение. Числа r и  называются полярными координатами точки М: r называют полярным радиусом,  – полярным углом.

Если рассматривать значения r в промежутке [0; +), а значение  в (–; ] (или в [0; 2)), то каждой точке плоскости (кроме О) соответствует единственная пара чисел r и , и наоборот.

Если совместить полюс О с началом координат системы Oxy, а полярную ось – с положительной полуосью Oxy (рис. 4.16), то связь между полярными и прямоугольными координатами точки (кроме точки О) устанавливается формулами:

и

Откуда, в частности, , где .

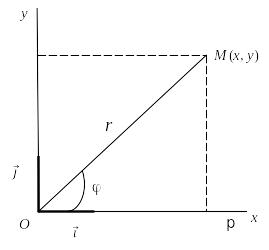
Рис. 4.16

П ример 4.32. Найти прямоугольные координаты точки М с полярными координатами .

Решение. Имеем . По формулам (4.31) находим

.

И так, .

П ример 4.33. Найти полярные координаты точки М с прямоугольными координатами .

Р ешение. Имеем . По формулам (4.32) находим . Точка М лежит в III четверти, следовательно, с учетом того, что , получаем . Итак, .