
- •Часть 1
- •Оглавление
- •5. Введение в математический анализ 109
- •6. Дифференциальное исчисление функций одной переменной 121
- •7. Применение дифференциального исчисления для исследования функций и построения их графиков 144
- •Введение
- •1. Общие рекомендации студенту заочной формы обучения по работе над дисциплиной «математика»
- •Работа студента с учебником
- •Решение задач
- •Самопроверка
- •Консультации
- •Контрольные работы
- •Лекции и практические занятия
- •Зачеты и экзамены
- •2. Правила выполнения и оформления контрольных работ
- •3. Программа дисциплины «математика» на I семестр
- •3.1. Элементы линейной алгебры и аналитической геометрии
- •3.2. Введение в математический анализ
- •3.3. Дифференциальное исчисление функций одной переменной
- •3.4. Применение дифференциального исчисления для исследования функций и построения их графиков
- •4. Линейная алгебра и аналитическая геометрия
- •4.1. Матрицы. Основные определения. Операции над матрицами
- •4.2. Определители. Миноры и алгебраические дополнения
- •4.3. Обратная матрица
- •4.4. Ранг матрицы
- •4.5. Системы линейных уравнений. Основные понятия. Решение невырожденных линейных систем. Матричный метод. Формулы Крамера
- •Умножения уравнения системы на число, отличное от нуля;
- •Прибавления к одному уравнению другого, умноженного на любое число;
- •Перестановки местами двух уравнений системы.
- •4.6. Исследование систем линейных уравнений. Теорема Кронекера–Капелли. Метод Гаусса
- •4.7. Векторы. Линейные операции над векторами. Разложение векторов. Координаты вектора
- •4.8. Скалярное произведение векторов
- •4.9. Векторное произведение векторов
- •4.10. Смешанное произведение векторов
- •4.11. Полярная система координат. Уравнение линии на плоскости
- •4.11.1. Полярная система координат
- •4.11.2. Уравнение линии на плоскости
- •4.12. Прямая на плоскости
- •4.12.1. Различные виды уравнений прямой
- •4.12.2. Взаимное расположение прямых на плоскости
- •4.13. Плоскость в пространстве
- •4.13.1. Различные виды уравнения плоскости
- •4.13.2. Взаимное расположение плоскостей
- •4.14. Прямая в пространстве
- •4.14.1. Различные уравнения прямой в пространстве
- •4.14.2. Взаимное расположение прямых в пространстве
- •4.15. Прямая и плоскость в пространстве
- •4.16. Кривые второго порядка
- •4.16.1. Окружность
- •4.16.2. Эллипс
- •4.16.3. Гипербола
- •4.16.4. Парабола
- •4.17. Поверхности второго порядка
- •4.17.1. Цилиндры и конусы
- •4.17.2. Канонические уравнения поверхностей второго порядка
4.8. Скалярное произведение векторов
Определение.
Скалярным
произведением ненулевых
векторов
и
называется число, которое обозначается
![]() или
или
![]() и определяется равенством
и определяется равенством

т. е. число,
равное произведению длин этих векторов
на косинус угла
![]() между ними. По определению
между ними. По определению
![]() .
.
Скалярное произведение обладает следующими свойствами:
1) ![]() (коммутативность);
(коммутативность);
2) ![]() (дистрибутивность);
(дистрибутивность);
3) ![]() (ассоциативность относительно скалярного
множителя);
(ассоциативность относительно скалярного
множителя);
4) ![]() (или
(или
![]() или
или
![]() )
(критерий ортогональности);
)
(критерий ортогональности);
5) ![]() (скалярный квадрат вектора);
(скалярный квадрат вектора);
6) ![]() .
.
Если векторы
и
заданы координатами в ортонормированном
базисе
![]() ,
то
,
то
1) ![]() ;
;
2) ![]() (следует из свойства 5);
(следует из свойства 5);
3)  (вытекает из формулы (4.29) и формул для
вычисления
(вытекает из формулы (4.29) и формул для
вычисления
![]() и
и
![]() ).
).
4)  (следует из свойства 6).
(следует из свойства 6).
Механический смысл скалярного произведения – это работа А, производимая силой , точка приложения которой перемещается по отрезку М1М2 из точки М1 в точку М2:
![]() .
.
П ример
4.23. Даны векторы
ример
4.23. Даны векторы
![]() Найти
Найти
![]() .
.
Решение.
Так как
векторы
![]() заданы координатами в ортонормированном
базисе
заданы координатами в ортонормированном
базисе
![]() ,
а
,
а
![]() то
то
![]() .
.
Поэтому
![]() .
.
О твет:
твет:
![]() .
.
П ример
4.24. Найти
ример
4.24. Найти
![]() ,
если
,
если
![]() ;
;
![]() .
.
Решение. Используя свойства 1, 2, 3, 5 скалярного произведения, имеем:

О твет:
– 34.
твет:
– 34.
П ример
4.25. Какую работу производит сила
ример
4.25. Какую работу производит сила
![]() ,
когда точка ее приложения, двигаясь
прямолинейно, перемещается из точки
,
когда точка ее приложения, двигаясь
прямолинейно, перемещается из точки
![]() в точку
в точку
![]() ?
?
Решение.
Используя
механический смысл скалярного
произведения, имеем
![]() .
.
Найдем координаты вектора :
![]() .
.
Тогда
![]() .
.
О твет:
20.
твет:
20.
4.9. Векторное произведение векторов
Определение. Векторным произведением вектора и вектора называется вектор , удовлетворяющий трем условиям:
1)
![]() ;
;
2)
![]() ;
;
3) упорядоченная
тройка векторов
![]() – правая (рис. 4.12).
– правая (рис. 4.12).
Обозначение: ![]() или
или
![]() .
.
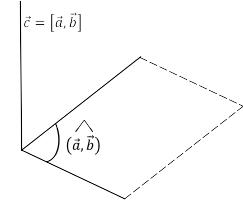
Рис. 4.12
Векторное произведение обладает следующими свойствами:
1)
![]() (антикоммутативность);
(антикоммутативность);
2)
![]() (дистрибутивность);
(дистрибутивность);
3)
![]() (ассоциативность относительно скалярного
множителя);
(ассоциативность относительно скалярного
множителя);
4)
![]() (критерий коллинеарности);
(критерий коллинеарности);
5) геометрический
смысл векторного
произведения: модуль векторного
произведения
![]() равен площади
параллелограмма,
построенного на векторах
и
,
отложенных от одной точки:
равен площади
параллелограмма,
построенного на векторах
и
,
отложенных от одной точки:
![]() ;
;
6) механический
смысл
векторного произведения: момент
силы
,
приложенной в точке В,
относительно точки А
определяется равенством:
![]() .
.
Если векторы
и
заданы в ортонормированном базисе
![]() координатами
координатами
![]() ,
то
,
то


Пример 4.26. Найти площадь и длину высоты BD треугольника с вершинами в точках А(1, –2, 8), В(0, 0, 4), С(6, 2, 0).
Решение.
Поскольку площадь S
треугольника АВС
равна
![]() ,
то
,
то
![]() (рис. 4.13).
(рис. 4.13).

Рис. 4.13
1. Находим координаты
векторов
![]() и длину
и длину
![]() вектора
вектора
![]() :
:
![]()
![]()
2. Находим S:

3 .
.
![]()
П ример 4.27. Сила
ример 4.27. Сила
![]() приложена в точке В(0; 1; –2).
Найти
приложена в точке В(0; 1; –2).
Найти
![]() ,
если А(1; –1; 2).
,
если А(1; –1; 2).
Решение. Согласно
определению момента силы
,
находим координаты вектора
![]() ,
тогда
,
тогда
 .
.
О твет:
твет:
![]() .
.
П ример
4.28. Найти
единичный вектор
,
перпендикулярный каждому из векторов
ример
4.28. Найти
единичный вектор
,
перпендикулярный каждому из векторов
![]() и
и
![]() .
.
Решение. Векторное произведение даст вектор, который ортогонален каждому из векторов и . Найдем (см. (4.30)):
 .
.
Тогда
 .
.
О твет:
твет:
![]() .
.
