Методические указания Как подготовится к итоговому компьютерному тестированию по физике?

Здесь представлены некоторые задания по семи дидактическим единицам, составляющим курс физики. В методических указаниях рассмотрены подробные решения тестовых заданий, а также даны задания для самостоятельной работы студентов. Также по некоторым темам дан теоретический материал, подготовленный по лекциям д. ф.-м. н. Афанасьева А.Д. для самоподготовки советую использовать учебник Т.М. Трофимовой «Курс физики»

Первая де «Механика»

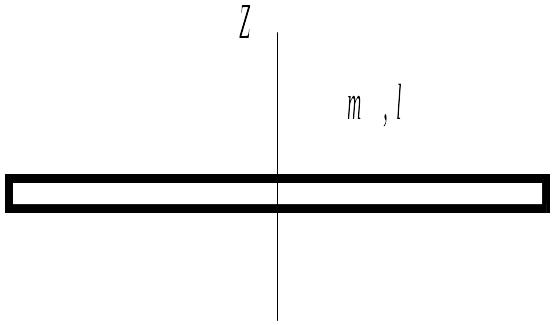
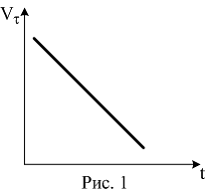
Материальная точка M движется по окружности со скоростью . На рис.1 показан график зависимости проекции скорости от времени ( – единичный вектор положительного направления, – проекция на это направление). При этом вектор полного ускорения на рис.2 имеет направление

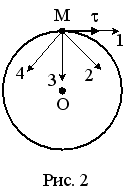
ВАРИАНТЫ ОТВЕТОВ:

1) 1 2) 3

3) 2 4) 4

Тут все просто, скорость уменьшается и единственный возможный вариант 4-ый.

Р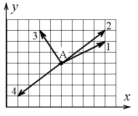 адиус-вектор частицы изменяется во времени по закону . В момент времени t=1с частица оказалась в некоторой точке А. Выберите правильное направление скорости частицы в этот момент времени.

а) 1 б) 2 в) 3 г) 4

д) на рисунке нет правильного направления

Здесь следует помнить , следовательно , тогда в момент t=1c , . Полученным координатам удовлетворяет вариант «2», координаты отсчитывать от точки А. Здесь возможны различные вариации ,в частности найти ускорение, поступаем аналогично .

Т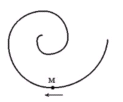 очка М движется по спирали с постоянной по величине скоростью в направлении, указанном стрелкой. При этом величина нормального ускорения ...

1) увеличивается 2) уменьшается 3) не изменяется

Величина нормального ускорения определяется , как видно из рисунка радиус уменьшается в процессе движения, следовательно, ускорение увеличивается.

М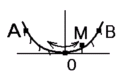 атериальная точка M свободно без трения скользит в поле силы тяжести по гладким стенкам симметричной ямы (A и B – наивысшие точки подъема). При этом величина тангенциальной (касательной к траектории) проекции ускорения точки М:

а) отлична от нуля в точке В; б) максимальна в нижней точке траектории О; в) равна нулю в точке А; г) одинакова во всех точках траектории;

К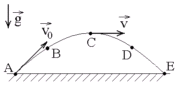 амень бросили под углом к горизонту со скоростью V₀. Его траектория в однородном поле тяжести изображена на рисунке. Сопротивления воздуха нет. Модуль тангенциального ускорения на участке А-В-С:

1) уменьшается 2) увеличивается 3) не изменяется

Тангенциальное ускорение отвечает за изменение модуля скорости (а нормальная компонента ускорения за изменение направления скорости), тогда модуль скорости в процессе подъема уменьшается, тогда и ускорение тоже уменьшается.

Д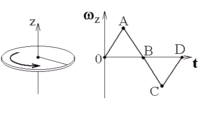 иск вращается вокруг своей оси, изменяя проекцию своей угловой скорости так, как показано на рисунке. На каких участках графика зависимости вектор угловой скорости и вектор углового ускорения направлены в одну сторону?

1) 0 - А и А-В 2) 0-А и В–С

3) В - С и С - D 4) всегда направлены в одну сторону

Вектор угловой скорости и вектор углового ускорения направлены в одну сторону в случае равноускоренного движения, когда и , и имеют один и тот же знак. Сразу очевидно, что это участок 0-А, а также участок В-С.

Предлагаю решить некоторые задачи самостоятельно, небольшая теоретическая шпаргалка.

Кинематика вращательной точки. Угловая скорость.

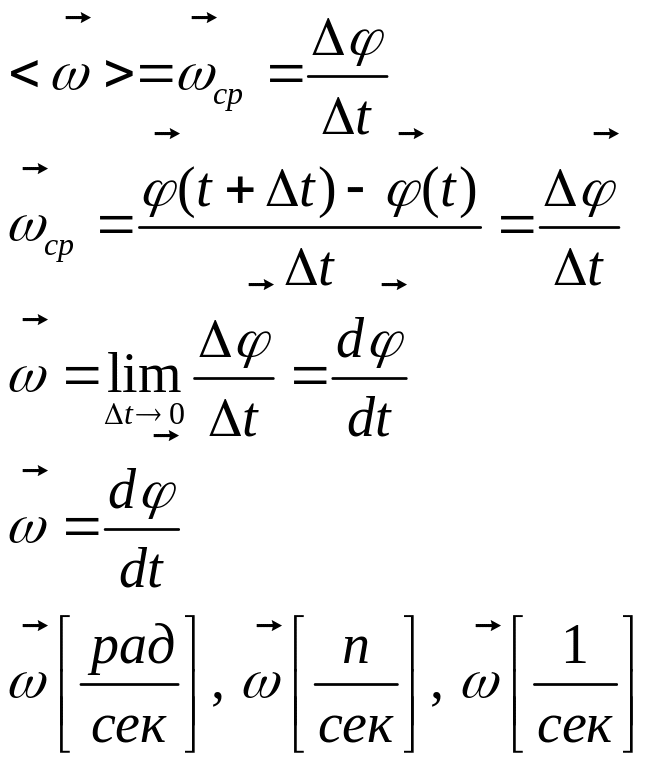
n – число оборотов.

Если w=const, то w - круговая (циклическая) частота. _, Т – период (время одного оборота). - линейная частота. Модуль равен углу поворота и направлен по оси вращения так, что направление поворота отвечает правилу винта.

- угловое ускорение.

1. При равноускоренном движении вектор направлен в ту же сторону что и .

2. При равнозамедленном – в обратную.

Вектора r, v и a называют естественными или полярными векторами.

Вектора - аксиальными.

Аксиальные вектора введены для объяснения физических процессов при вращательном движении. Они, так же как и полярные вектора подчиняются правилу сложения векторов.

Связь между линейными и угловыми величинами.

, r – радиус-вектор.

По определению векторного произведения .

a_n=a_ц – изменение скорости по направлению за единицу времени.

a_t – изменение скорости по модулю за единицу времени. При равномерном движении a_t=0.

Т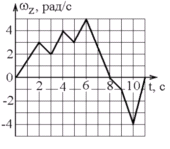 вердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. В какой момент времени угол поворота тела относительно начального положения будет максимальным? а) 8с б) 6с в) 11с г) 10с

Д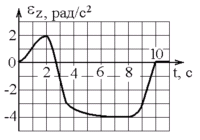 иск радиуса R начинает вращаться из состояния покоя в горизонтальной плоскости вокруг оси Z, проходящей перпендикулярно его плоскости через его центр. Зависимость проекции углового ускорения от времени показана на графике. Во сколько раз отличаются величины тангенциальных ускорений точки на краю диска в моменты времени t₁ = 2 с и t₂ = 7 с? а) в 2 раза б) в 4 раза в) оба равны нулю г) трудно определить точно

Т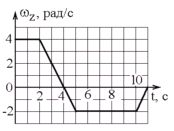 вердое тело начинает вращаться вокруг оси Z с угловой скоростью, проекция которой изменяется во времени, как показано на графике. На какой угол относительно начального положения окажется повернутым тело через 11 секунд?

а) 8 рад б) 12 рад в) 24 рад г) 0 рад.

В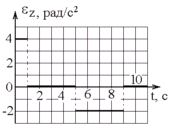 начальный момент времени t = 0 твердому телу придали угловую скорость рад/с вокруг оси Z и в дальнейшем тело испытывает угловое ускорение, проекция которого изменяется со временем, как показано на графике. В какой момент времени тело изменит направление своего вращения?

а) 8 с б) 1 с в) 2 с г) 9 с

Частица движется вдоль окружности с радиусом 1 м в соответствии с уравнением, где - угол в радианах, - время в секундах. Величина нормального ускорения частицы равна нулю в момент времени (в секундах), равный: а) 1 б) 2 в) 3 г) 4

Еще небольшая шпаргалка

Законы Ньютона.

Первый закон Ньютона. Тело, достаточно удаленное от других тел, сохраняет состояние покоя или равномерного прямолинейного движения.

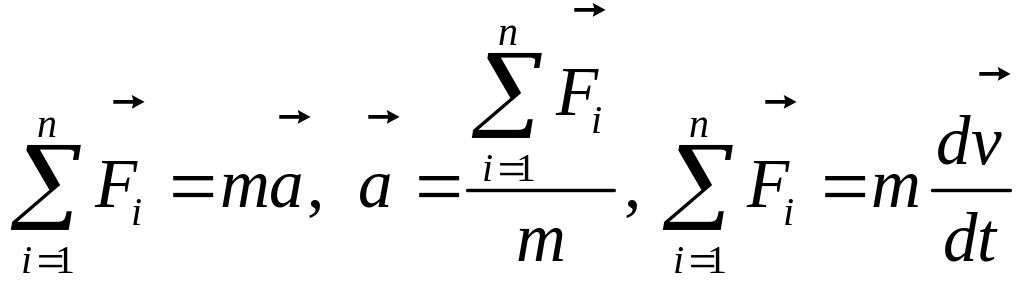
Если , то .

Первый закон Ньютона является независимым законом, выражающим критерий пригодности системы отсчета для рассмотрения движения. Это закон является первым в порядковом смысле, потому что только после него можно говорить о точно определенном физическом смысле и содержании второго и третьего законов.

Второй закон Ньютона:

Физическое содержание этого закона состоит в том, что сила определяет вторые производные координат по времени.

Производная импульса тела по времени равна результирующей силе и совпадает с ней по направлению.

Изменение импульса равно изменению суммы внешних сил.

Третий закон Ньютона. Силы взаимодействия двух материальных точек равны по величине, противоположны по направлению и действуют вдоль прямых, соединяющих эти точки.

Пусть взаимодействуют и .

В изолированной системе сумма импульсов постоянна.

Пример: Стакан падает на бетонный пол или на ковер.

. Чем меньше время взаимодействия, тем больше сила.

И з-за неисправности мотора величина скорости автомобиля синусоидально изменялась во времени, как показано на графике зависимости V(t). В момент времени t₁ автомобиль поднимался по участку дуги. Куда может быть направлена результирующая всех сил, действующих на автомобиль в этот момент времени? 1) 1 2) 2 3) 3 4) 4 5) 5

М атериальная точка M движется по окружности со скоростью . На рис.1 показан график зависимости проекции скорости на орт , направленный вдоль скорости. На рис.2 укажите направление силы, действующей на точку M в момент времени t₁:

а) 1 б) 2в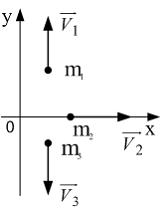 ) 3 г) 4

Система состоит из трех шаров c массами m₁=1кг, m₂=2кг, m₃=3кг, которые движутся так, как показано на рисунке.

Если скорости шаров равны v1=3м/с, v2=2м/с, v3=1м/с, то величина скорости центра масс этой системы в м/c равна…

ВАРИАНТЫ ОТВЕТОВ:

1) 4 2) 3) 10 4) .

Тут тоже все просто

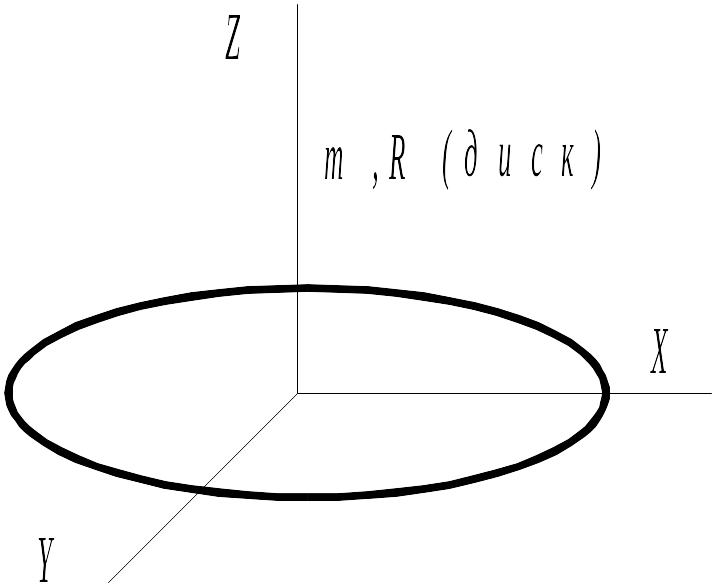
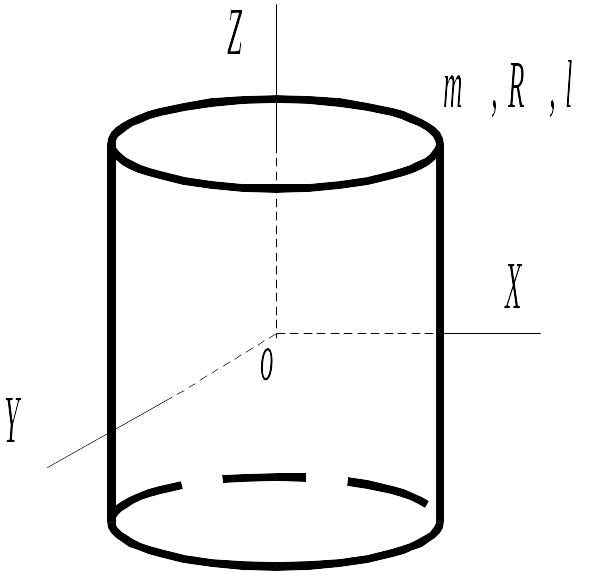
Д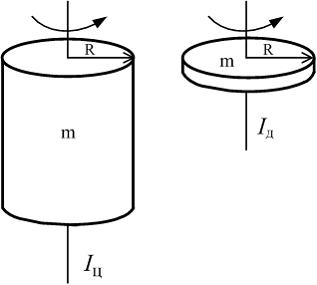 иск и цилиндр имеют одинаковые массы и радиусы (рис.). Для их моментов инерции справедливо соотношение…

ВАРИАНТЫ ОТВЕТОВ:

1) Iц=Iд 2) Iц>Iд 3) Iц<Iд

Здесь важно помнить, хотя кому это надо помнить, как определяются моменты инерции твердых тел.

Даю табличку, пригодится.

Моменты инерции тел, имеющих простую геометрическую форму

Форма тела	Моменты инерции

Видим, что диск, что цилиндр все едино.

Еще возможный вариант задачи на момент инерции, здесь надо знать теорему Штейна, . Из рисунка видно (прочтите для начала условие), что минимальным моментом инерции будет обладать (неразрезанный). Дальше варианты 2 и 3. Разрез вдоль оси вращения момент инерции увеличит (смотри теорему), а вот разрез поперек оси на момент инерции никак не повлияет. Так что вариант (1).

Из жести вырезали три одинаковые детали в виде эллипса. Две детали разрезали: одну - пополам вдоль оси симметрии, а вторую - на четыре одинаковые части. Затем все части отодвинули друг от друга на одинаковое расстояние и расставили симметрично относительно оси OO' (см. рис.). Выберите правильное соотношение между моментами инерции этих деталей относительно оси OO'.

1) 2) 3)

В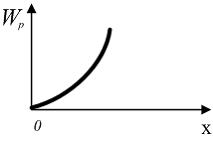 потенциальном поле сила  пропорциональна градиенту потенциальной энергии . Если график зависимости потенциальной энергии  от координаты x имеет вид, представленный на рисунке, то зависимость проекции силы  на ось X будет….

ВАРИАНТЫ ОТВЕТОВ:

1)  2) 3) 4)

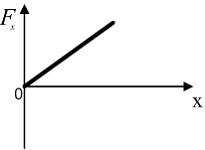
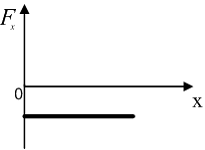
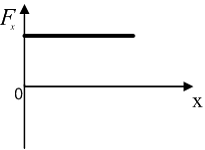
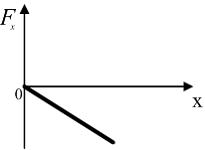
. Производная от параболы прямая, добавляя знак минус, получаем убывающую зависимость – вариант «4».

Из этой же оперы такая задача:

Момент импульса тела относительно неподвижной оси изменяется по закону .Укажите график, правильно отражающий зависимость от времени величины момента сил, действующих на тело.

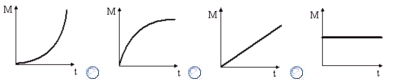
1) 2) 3) 4)

Здесь почти как в предыдущей задаче . Кто сомневается, домножте векторно правую и левую часть выражения на - радиус вектор и вспомните определение момента силы и момента импульса. Тогда получим, что производная от квадрата – прямая - -, проходящая через начало координат. Единственный возможный вариант 3.

Теннисный мяч летел с импульсом  в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 0,1 с. Изменившийся импульс мяча стал равным  (масштаб указан на рисунке). Средняя сила удара равна …

Д ля начала разберемся что нам известно. Известны координаты векторов и , соответственно координаты . Модуль вектора . Ну а сила тогда .

ВАРИАНТЫ ОТВЕТОВ: 1) 5 Н 2) 0,5 Н 3) 50 Н 4) 30 Н

И 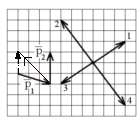мпульс тела изменился под действием короткого удара и стал равным, как показано на рисунке. В каком направлении действовала сила?

тут из физики надо знать только то, что сила совпадает с направлением изменения импульса. Определяем направление вектора , смотрим на варианты ответов и отмечаем «2»

а) 1 б) 2 в) 3 г) 4

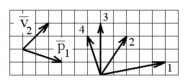Импульс тела изменился под действием короткого удара, и скорость тела стала равной, как показано на рисунке. В каком направлении могла действовать сила?

а) 2, 3, 4 б) 1 в) только 4 г) 1, 2

Т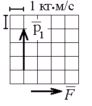 еннисный мяч летел с импульсом (масштаб и направления указаны на рисунке). В перпендикулярном направлении на короткое время 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40Н. Какова стала величина импульса после того, как ветер утих?

а) 5 б) 0,5 в) 43 г) 50 д) 7

В таком классе задач важно знать определение силы через импульс и уметь работать с векторами.

Итак, импульс – величина векторная, равная произведению массы тела (мат. точки) на скорость тела (мат. точки) ; направление импульса совпадает с направлением скорости.

Под действием силы импульс можно изменить , направление силы будет совпадать с направлением .

Модуль вектора (любого) определяется как .

Потенциальные силы.

Два класса сил:

1. Работа не зависит от пути;

2. Работа зависит от пути;

Пример:

1. Работа в поле тяжести;

2. Сухое трение;

Силы, работа которых зависит лишь от начальной и конечной точки траектории, но не зависит от ее вида, называются потенциальными.

Потенциальные силы – потенциальные поля.

По определению потенциального поля:

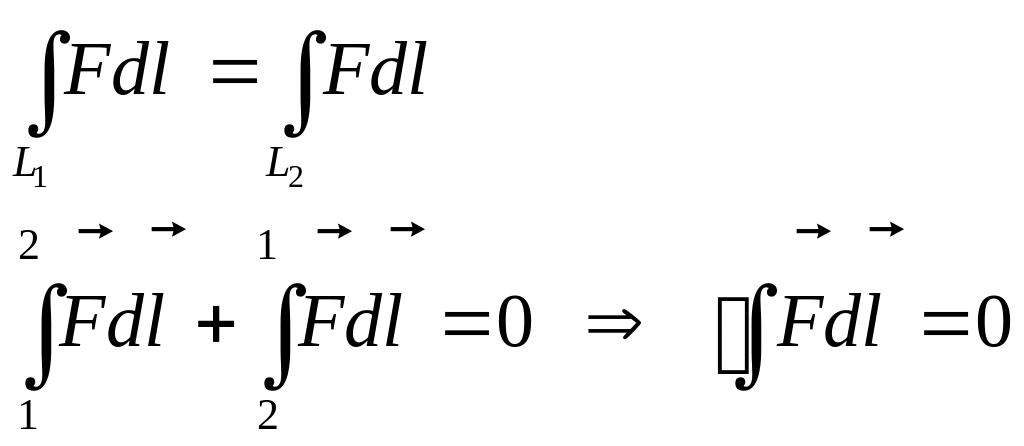
Потенциальным называется поле, в котором работа сил поля по замкнутому контуру равна 0.

Чтобы поле было потенциальным необходимо и достаточно, чтобы работа сил поля по любому контуру была равна 0.

Работа в потенциальном поле.

Если смещение происходит вдоль одной координатной оси, то

Для консервативных сил

Или

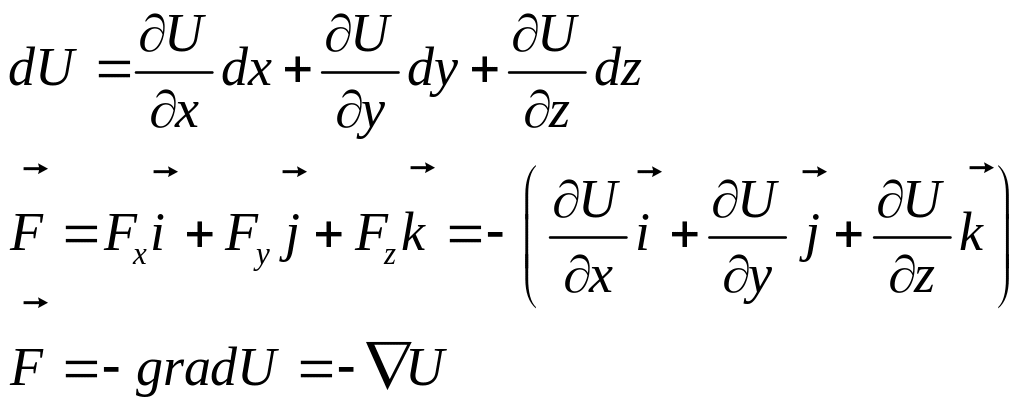
Сила поля равна взятому со знаком минус градиенту потенциальной энергии частицы в этой точке поля.

Понятие градиента.

Для выяснения смысла градиента возьмем эквипотенциальные поверхности.

Переходим от 1 к 2 по нормали.

Обозначим

Градиент функции есть вектор, направленный по нормали к поверхности уровня в сторону возрастания U, его длина равна по нормам функции к той же поверхности.

Примеры:

Нормировка потенциальной энергии.

Если вместо взять другую функцию , то есть измененную на всем пространстве, то сила не изменится.

Потенциальная энергия определена с точностью до постоянной.

Процедура придания потенциальной энергии однозначности называется нормировкой.

Нуль на поверхности Земли.

Кинетическая энергия.

Работа силы при поступательном движении материальной точки равна приращению кинетической энергии этой точки.

Законы сохранения.

Механическая задача считается решенной, если известно положение движущейся частицы в любой момент времени.

Закон сохранения импульса.

Импульс изолированной системы не изменяется при любых процессах происходящих внутри системы.

В релятивистском случае: так как не существует центра масс, то его нельзя интерпретировать как равномерное и прямолинейное движение центра масс. Не существует системы отсчета центра масс, в котором импульс равен 0. Это означает, что при любых процессах внутри нее эта система остается системой центра масс.

Закон сохранения момента импульса.

Для изолированной системы:

В инерциальной системе отсчета момент импульса изолированной системы остается постоянным при любых процессах, происходящих внутри системы.

У незамкнутых систем может сохраняться не сам момент импульса, а его проекция на некоторую неподвижную ось.

Например, если система движется в однородном поле силы тяжести вертикальной оси

Закон сохранения энергии в нерелятивистском случае.

Пусть m₀ движется под действием F.

(3)

Умножая (3) на v, получаем:

но или .

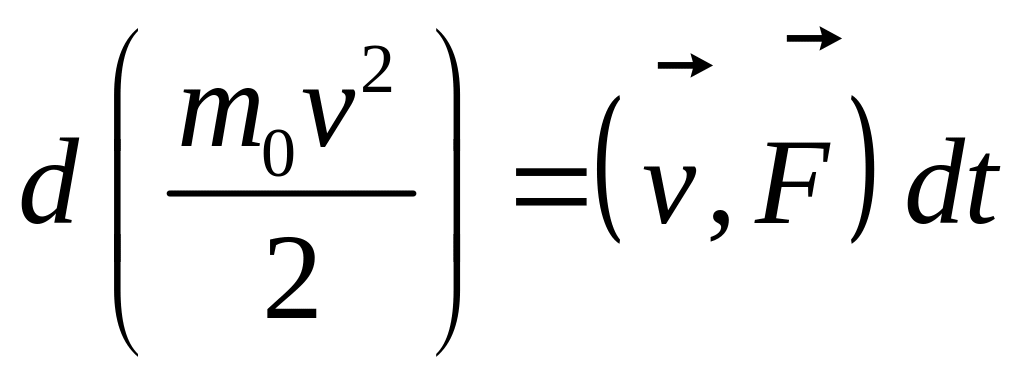Проинтегрируем:

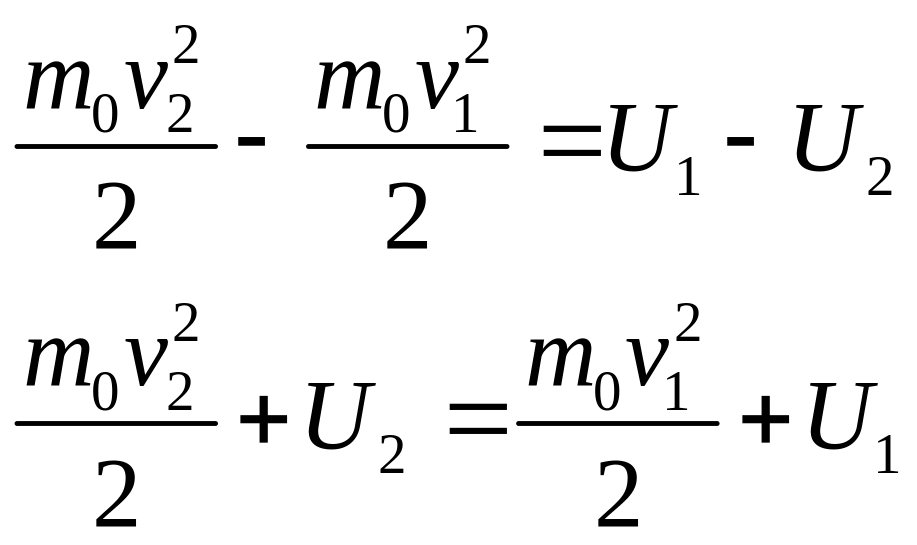
То есть сумма кинетической и потенциальной энергий при движении остается постоянной.

Кинематика твердого тела.

Твердое тело – идеализированная система материальных точек, все расстояния между которыми при движении системы не изменяются с течением времени.

Число степеней свободы – число независимых координат, необходимых для описания местоположения тела.

Поступательные степени свободы (трансляционные) i=3.

Вращательные степени свободы

1. Одноатомная частица i=0.

2. Двухатомная частица i=2.

3. Трехатомная частица i=3.

1. 

2. 

3. 

Твердое тело из N молекул (частиц) казалось бы, имеет 3N координат. Но оказывается, 3N-6 из них зависимы (так как они закреплены относительно друг друга).

Чтобы закрепить твердое тело необходимо задать минимум 3 точки не лежащие на одной прямой.

Пять видов движения твердых тел.

1. Поступательное движение.

2. Вращательное движение вокруг неподвижной оси.

3. Плоское движение.

4. Движение вокруг неподвижной точки.

5. Свободное движение.

1) и 2) – основные.

1. Поступательное движение – движение, при котором любая прямая, связанная с телом, всегда остается параллельной своему начальному положению. Скорости всех точек тела в любой момент времени одинаковы.

2. Вращательное движение вокруг неподвижной оси – движение, при котором две точки тела всегда остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела на этой оси неподвижны. Остальные точки движутся по окружностям в плоскости, перпендикулярным оси вращения с центрами на этой оси.

Мгновенная ось вращения.

Р ассмотрим качение обруча без скольжения. Следовательно, точка касания A в рассматриваемый момент времени неподвижна. То есть, движение обруча можно рассматривать как вращение его мгновенной оси вращения, проходящей через точку касания A. Мгновенная ось – воображаемая ось. Малый поворот тела вокруг точки касания A.

Уравнения, описывающие движение твердого тела.

Р ассмотрим кинематику движения твердого тела. Произвольное бесконечно малое перемещение твердого тела является результатом двух движений:

1. Параллельный перенос тела, при котором центр масс тела смещается поступательно на некоторое расстояние без изменения ориентации.

2. Малый поворот тела вокруг центра масс – вращающая составляющая.

Радиус-вектор любой точки может быть представлен в виде:

радиус-вектор центра масс и положение точки в теле.

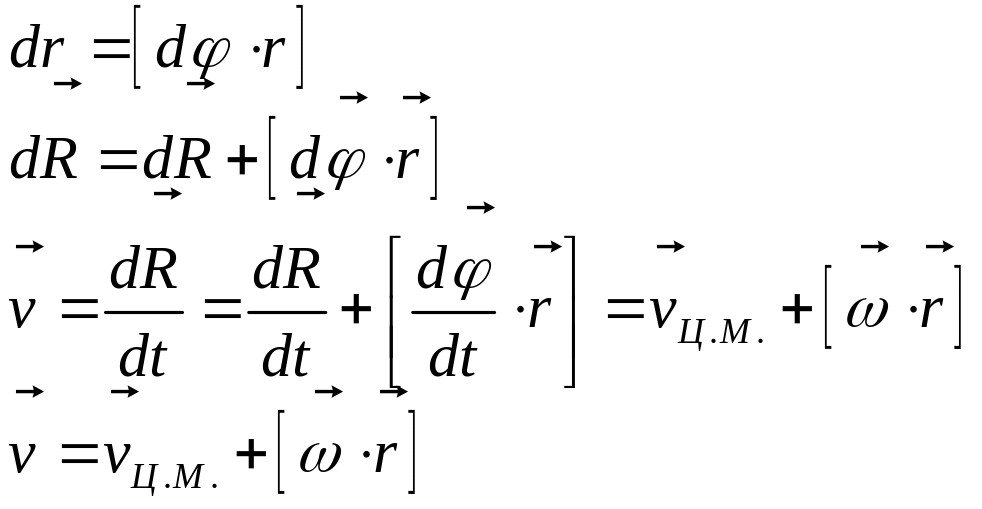
Скорость точки в твердом теле равна сумме скорости поступательного движения и линейной скорости углового вращения.

Динамика.

Определить, как проходят изменения 6 величин:

Углы являются абсолютной характеристикой в том смысле, что он не зависит от того, относительно какой точки рассматривается вращение.

Если центр вращения совпадает с центром масс, то выполняется уравнение моментов.

Д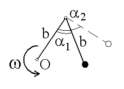 ва невесомых стержня длины b соединены под углом a₁ = 60° и вращаются без трения в горизонтальной плоскости вокруг вертикальной оси О с угловой скоростью w. На конце одного из стержней прикреплен очень маленький массивный шарик. В некоторый момент угол между стержнями самопроизвольно увеличился до a₂ = 90°. С какой угловой скоростью стала вращаться такая система?

1) w 2) 2w 3) 2w 4) 5)

В начальный момент времени тонкий обруч с массой и с радиусом не вращался, а поступательно скользил по горизонтальной поверхности с кинетической энергией 800 Дж. Под действием силы трения он начал катиться без проскальзывания с кинетической энергией поступательного движения 200 Дж. Сила трения совершила работу:

а) 300Дж б) 600Дж в) 500Дж г) 400 Дж

По закону сохранения энергии, энергия никуда не исчезает и не появляется вновь, она лишь переходит из одного вида энергии в другой.

Тогда наш 800Дж ( ), будет расходоваться на работу сил трения( ), кинетическую энергию поступательного движения( ) и кинетическую энергию вращательного движения ( ).

Запишем ЗСЭ: , отсюда

, т.к. , , . Подставляем все возможное и получаем

Сплошной и полый (трубка) цилиндры, имеющие одинаковые массы и радиусы, вкатываются без проскальзывания на горку. Если начальные скорости тел одинаковы, то ...

а) выше поднимется сплошной цилиндр

б) оба тела поднимутся на одну и ту де высоту

в) выше поднимется полый цилиндр

Согласно закону сохранения энергии: вся кинетическая энергия тела должна перейти в потенциальную. . Если обе системы имеют одинаковые параметры (масса и радиус), то моменты инерции, скорости таких тел одинаковы и, следовательно, они будут подниматься на одну и ту же высоту.

Д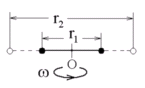 ва маленьких массивных шарика закреплены на невесомом длинном стержне на расстоянии r₁ друг от друга. Стержень может вращаться без трения в горизонтальной плоскости вокруг вертикальной оси, проходящей посередине между шариками. Стержень раскрутили из состояния покоя до угловой скорости w, при этом была совершена работа А₁. Шарики раздвинули симметрично на расстояние r₂ = 2r₁ и раскрутили до той же угловой скорости. Какая работа при этом была совершена?

1 ) А₂= А₁ 2) А₂=2А₁ 3) А₂= А₁ 4) А₂ = 4А₁

Д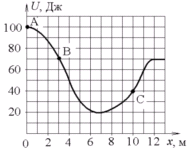 ля того, чтобы раскрутить диск радиуса R₁ вокруг своей оси до угловой скорости w, необходимо совершить работу А₁. Под прессом диск становится тоньше, но радиус его возрастает до R₂=2R₁. Какую работу надо совершить, чтобы раскрутить его до той же угловой скорости? Трением пренебречь.

1) А₂= А₁ 2) А₂=2А₁ 3) А₂= А₁ 4) А₂=4А₁

Небольшая шайба начинает движение без начальной скорости по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии шайбы от координаты х изображена на графике . Кинетическая энергия шайбы в точке С.

а) в 2 раза больше, чем в точке В

б) в 2 раза меньше, чем в точке В

в) в 1,75 раза больше, чем в точке В

г)в 1,75 раза меньше, чем в точке В

Тело массы m=10кг начинает движение со скоростью =4м/с по гладкой ледяной горке из точки А. Сопротивление воздуха пренебрежимо мало. Зависимость потенциальной энергии этого тела от координаты х изображена на графике . В точке В тело, ударившись, прилипает к стене. В результате абсолютно неупругого удара в точке В выделилось ... теплоты

а) 140Дж б) 160Дж в) 20Дж г) 150Дж

П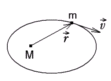 ланета массой m движется по эллиптической орбите, в одном из фокусов которой находится звезда массы . - радиус-вектор планеты (см.рисунок). Выберите правильное утверждение:

а) момент импульса планеты относительно центра звезды меняется и максимален при наибольшем ее удалении от звезды

б) момент силы тяготения, действующей на планету (относительно центра звезды), изменяется при движении планеты по орбите, но направлен перпендикулярно плоскости орбиты

в) величина момента импульса планеты относительно центра звезды в любой момент времени определяется выражением

г) момент импульса планеты относительно центра звезды при её движении по орбите не изменяется

Задачи про то как космические корабли бороздят просторы вселенной и про то, что в них творится.

Хочу вам напомнить кое-что

Преобразования Лоренца		Преобразования Галилея
Инвариантные	Вариантные	Инвариантные	Вариантные
			Координаты Скорости

Сокращение поперечных размеров тел, при измененности продольных означает изменение скорости тела.

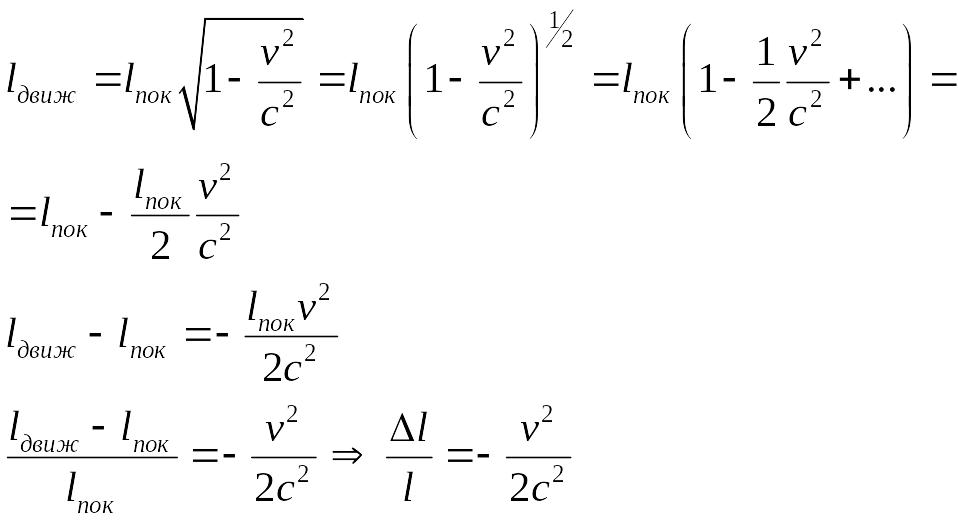
Н а борту космического корабля нанесена эмблема в виде геометрической фигуры. Из-за релятивистского сокращения длины эта фигура изменяет свою форму. Как она будет выглядеть для неподвижного наблюдателя, если корабль движется в направлении, указанном на рисунке стрелкой, со скоростью, сравнимой со скоростью света?

1) А 2) В 3) С

При решении подобных задач внимательно читайте условие (этот совет примите как аксиому для решения любых задач). Изменение длину увидит только неподвижный наблюдатель, правильнее будет сказать наблюдатель в неподвижной системе отсчета.

Космический корабль с космонавтом летит со скоростью (с - скорость света в вакууме) мимо наблюдателя на неподвижной планете. Космонавт медленно поворачивает метровый стержень из положения «1», параллельного направлению движения его корабля, в положение «2», перпендикулярное этому направлению. Тогда длина стержня с точки зрения неподвижного наблюдателя :

а) изменится от 1,0м в положении «1» до 0,6м в положении «2»

б) изменится от 0,6м в положении "1" до 1,0м в положении "2"

в) равна 1,0м при любой ориентации стержня

г) изменится от 1,0м в положении «1» до 1,67м в положении «2»

, только для неподвижного наблюдателя

Космический корабль с двумя космонавтами летит со скоростью V=0,8c (c – скорость света в вакууме). Один из космонавтов медленно поворачивает метровый стержень из положения 1, параллельного направлению движения, в положение 2, перпендикулярное этому направлению. Тогда длина стержня с точки зрения другого космонавта …