14.2. Непрерывный вейвлет-анализ.

Основные приложения непрерывного вейвлет-анализа: локализация и классификация особых точек сигнала, частотно-временной анализ нестационарных сигналов. Глобальная задача сжатия информации – сократить этот объем при сохранении приемлемого качества. В этом существенную роль и играет вейвлет-анализ.

Фактически, для того, чтобы функция ψ(t) могла принадлежать к классу вейвлетов, необходимо выполнение двух условий:

1. График функции ψ(t) должен быть локален и осцилировать вокруг нуля в окрестности некоторой точки на оси времени, и резко убывать при

t → ± ∞; при этом ее среднее значение (т.е. интеграл по времени) равно нулю:

; (14.1)

2. Норма функции (ее энергия) должна быть конечной:

(14.2)

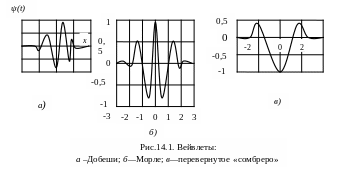
В радиотехнике непрерывный вейвлет-анализ часто осуществляется с помощью трех функций (рис. 14.1). Это вейвлеты Добеши, Морле и перевернутое «сомбреро».

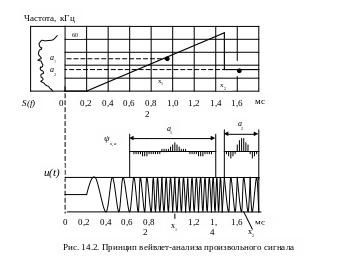
Возмем произвольный непериодический сигнал неизменной амплитуды u(t) (ЛЧМ-сигнал) и в упрощенной форме произведем его вейвлет-анализ при помощи вейвлета «сомбреро» (рис. 14.1), причем переменную х назовем временем. Результатом вейвлет-анализа этого сигнала будет функция

W_u(x,a), которая зависит уже от двух переменных – от времени х и некоторого масштаба осциляции а.

Непрерывное вейвлет-преобразование сигнала u(t) определяется с помощью произвольной функции вейвлета ψ(х) и выглядит таким образом

W_u(x,a) = (14.3)

В нижней части рисунка изображен график исследуемого сигнала, в верхней в виде ломанной линии – распределение значений W_u(x,a) (по горизонтали – переменная х, по вертикали – ось а. Прямоугольниками изображены графики вейвлета ψ_x,a при разных значениях х и а (х₁, а₁ и х₂, а₂). Выделенные участки графика исходного сигнала u(t) поточечно умножаются на значения оказавшихся над ними столбиков, потом все это суммируется. Абсолютная величина суммы определяет, где будет координата (х,а) на верхней картинке ( на рисунке они выделены жирными точками). Это делается для всех пар (х,а). Параметр х является аналогом координаты времени t ( т.е. характеризует смещение сигнала во времени) а параметр а – аналогом периода осциляции ( т.е. обратной частоте а = 1/f). Значит вейвлет-преобразование W_u(x,a) содержит информацию о частотных и временн′ых или пространственных свойствах сигнала одновременно. Это и позволяет изучить сложный сигнал более детально, чем с помощью преобразования Фурье. Для сравнения слева на верхней части условно приведена спектральная плотность S(f)анализируемого сигнала. Наглядность этого представления совершенно не сравнима наглядностью вейвлет-преобразования. На рис. 14.2 видна наклонная кривая, по которой можно определить начальную частоту, конечную частоту и характер изменения локальной частоты колебаний.

14.3. Дискретный (ортогональный) вейвлет-анализ

Им называют представление дискретных сигналов в виде обобщенного ряда Фурье по системе ортогональных базисных функций, формирующихся из некоторого исходного (порождающего) вейвлета ψ(t) Применяется ортогональный вейвлет-анализ в основном для сжатия данных (информации) и подавления шумов.

В дискретном вейвлет-анализе применена музыкальная терминология. Набор значений вейвлет-преобразования при фиксированном масштабе а, называют голосом, диапазон масштабов (или, что то же самое, частот) от а до 2а, – октавой. Согласно музыкальной классике, на каждую октаву следует брать, по крайней мере, 12 голосов.

Упрощенно, идею многомасштабного дискретного вейвлет-анализа можно трактовать так: «большое» пространство «всех анализируемых сигналов» надо заполнить растянутыми или сжатыми копиями некоего «эталонного» пространства, порожденного элементарным сигналом ψ(х) и его сдвигами по оси времени. По определению это эталонное пространство принимается за набор сигналов, которые можно представить с разрешением 1.(Рис. 14.3).

Пусть функция φ(х) – исходный единичный заштрихованный «столбик» на интервале [0, 1]; его сдвиги – аналогичные столбики на интервалах ..., [-2, -1], [-1, 0], [1, 2],... (рис.14.3, а). Пространство сигналов (в нашем случае анализируемый сигнал u(t)) состоит из «лесенок», полученных умножением этих столбиков на определенные числа. Остальными пространствами сигналов служат перемасштабированные копии этих наборов столбиков. Одно из них получается растяжением вдвое – рис. 14.3, б). Для исходного сигнала φ(х) необходимо, чтобы, его сдвиги вида φ(х – 1), φ(х – 2), ... φ(х – k),... были друг другу ортогональны. В итоге получится

(14.4)

где h_k – некоторые коэффициенты.

В рассматриваемом примере для функции φ(х) коэффициенты h_k равны 1 и 1, а для ψ(х) соответственно 1 и –1.

Ортогональные вейвлеты замечательны тем, что существует быстрый алгоритм разложения по ним любого сигнала. Сам вейвлет показан на рис. 14.3, в и г; система его сдвигов и двоичных растяжений и сжатий – это широко известный базис на основании функций А.Хаара (A. Haar), разработанный им еще в 1909 г. (рис. 14.3, д)