Расчет переходных процессов с использованием спектрального метода

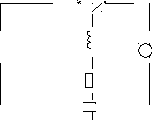
Определим ток переходного

процесса.

RLC-цепь, (рис. 7.25)

была подключена к источнику

э.д.с. e₁ (t) и в момент t = 0

переключается к источнику э.д.с. e(t)

Решение: Рис. 7.25

Найдем частотный спектр э.д.с. e(t):

Закон Ома для частотных спектров при ненулевых начальных условиях получим используя операторный метод при р = jw .

Знаменатель

представляет собой комплексное сопротивление RLC-цепи, применявшееся ранее для расчета установившихся (гармонических) процессов. При помощи z(jw) найдем спектр тока I (jw) , а и ток переходного процесса i(t) .

Пример

Найти ток при включении RC-цепи на экспоненциальное напряжение. (не параллельно RC-цепи). Определить АЧХ и функцию входного сигнала.

Решение:

, где a >0.

Прежде всего убедимся, что функцию u(t) можно представить интегралом Фурье. Функция u(t) абсолютно интегрируема в бесконечных пределах, т.к. интеграл

Конечен при любом a ¹ 0

Используя выражение

или по известному Лапласову изображению u(t) найдем ее частотный спектр

Следовательно, АЧХ и ФЧХ на входе:

Из этого следует, что включение апериодического u(t) можно рассматривать, как включение бесконечно большого числа элементарных гармонических колебаний, частоты которых изменяются от 0 до ¥ .

Комплексное сопротивление цепи

т.к. н.у. нулевые, то на основании закона для частотных спектров:

Операторное изображение тока:

Применим теорему разложения:

Корни

Вычислив значения множителей слагаемых теоремы разложения:

после простых преобразований получим:

Тот же результат можно получить при помощи обратного преобразования Фурье.

Этот пример показывает, что расчеты переходных процессов операторным и спектральным методом похожи друг на друга. Преимущества спектрального метода сказываются при экспериментально найденных входных сигналах и входных или передаточных функциях цепи.

Содержание:

ВВЕДЕНИЕ…………………………………………………………………………………..3

1. МЕТОДЫ АНАЛИЗА СЛОЖНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ПОСТОЯННОГО ТОКА………………………………………………………………………………………….7

ПОСЛЕДОВАТЕЛЬНОЕ И ПАРАЛЛЕЛЬНОЕ СОЕДИНЕНИЕ ЭЛЕМЕНТОВ………………………………………………………………………………...7

ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИ, СОДЕРЖАЩЕГО ЭДС…………………………8

ИСТОЧНИКИ ЭДС И ИСТОЧНИКИ ТОКА……………………………………………..12

РАЗВЕТВЛЕННЫЕ И НЕРАЗВЕТВЛЕННЫЕ ЦЕПИ………………………………….14

МЕТОД КОНТУРНЫХ ТОКОВ……………………………………………………………19

МЕТОД НАЛОЖЕНИЯ (СУПЕРПОЗИЦИИ)……………………………………………23

МЕТОД УЗЛОВЫХ ПОТЕНЦИАЛОВ……………………………………………………26

МЕТОД ДВУХ УЗЛОВ……………………………………………………………………..31

МЕТОДЫ, ОСНОВАННЫЕ НА ПРИМЕНЕНИИ ТЕОРЕМ ОБ ЭКВИВАЛЕНТНЫХ ИСТОЧНИКАХ………………………………………………………………………………32

ПРЕОБРАЗОВАНИЕ СХЕМЫ СОЕДИНЕНИЯ ЗВЕЗДА В ТРЕУГОЛЬНИК И ОБРАТНОЕ ПРЕОБРАЗОВАНИЕ……………………………………………………….42

2. АНАЛИЗ УСТАНОВИВШЕГОСЯ РЕЖИМА В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА…………………………………………………………………………………………46

ГАРМОНИЧЕСКИЕ ФУНКЦИИ…………………………………………………………..46

ИЗОБРАЖЕНИЕ СИНУСОИДАЛЬНО ИЗМЕНЯЮЩИХСЯ ВЕЛИЧИН НА КОМПЛЕКСНОЙ ПЛОСКОСТИ…………………………………………………………..47

МГНОВЕННАЯ МОЩНОСТЬ…………………………………………………………….49

СИНУСОИДАЛЬНЫЙ ТОК В АКТИВНОМ СОПРОТИВЛЕНИ (R)………………….49

ИНДУКТИВНОСТЬ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА…………………………51

КОНДЕНСАТОР В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА…………………………….52

МЕТОД КОМПЛЕКСНЫХ АМПЛИТУД………………………………………………….54

ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ МЕТОДА КОМПЛЕКСНЫХ АМПЛИТУД……….55

КОМПЛЕКСНЫЕ ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ………………………………...58

АНАЛИЗ ПРОСТЕЙШИХ ЛИНЕЙНЫХ ЦЕПЕЙ ПРИ ГАРМОНИЧЕСКОМ ВОЗДЕЙСТВИИ.ПОСЛЕДОВАТЕЛЬНАЯ RL-ЦЕПЬ…………………………………62

СОГЛАСОВАНИЕ ИСТОЧНИКА НАПРЯЖЕНИЯ С НАГРУЗКОЙ………………...69

РЕЗОНАНС В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.ПОСЛЕДОВАТЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР……………………………………………………………..73

ЗАТУХАНИЕ КОЛЕБАНИЙ В КОНТУРЕ………………………………………………..76

ПАРАЛЛЕЛЬНЫЙ КОЛЕБАТЕЛЬНЫЙ КОНТУР………………………………………81

РЕЗОНАНСНОЕ СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНОГО КОНТУРА……………..84

РАСШИРЕНИЕ ПОЛОСЫ ПРОПУСКАНИЯ КОНТУРА……………………………..87

КОНТУРЫ II И III ВИДОВ…………………………………………………………………90

РЕЗОНАНС В СЛОЖНЫХ ЦЕПЯХ……………………………………………………...93

ВЛИЯНИЕ ВНЕШНИХ ЦЕПЕЙ НА ХАРАКТЕРИСТИКИ КОНТУРА………………..97

3. МНОГОПОЛЮСНЫЕ ЦЕПИ………………………………………………………….102

УРАВНЕНИЯ ЧЕТЫРЕХПОЛЮСНИКА……………………………………………...103

КОЭФФИЦИЕНТЫ ЧЕТЫРЕХПОЛЮСНИКОВ………………………………………105

ОПРЕДЕЛЕНИЕ Y ПАРАМЕТРОВ……………………………………………………..108

УРАВНЕНИЯ СЛОЖНЫХ ЧЕТЫРЕХПОЛЮСНИКОВ В МАТРИЧНОЙ ФОРМЕ.110

МАТРИЦЫ НЕКОТОРЫХ ЧЕТЫРЕХПОЛЮСНИКОВ………………………………113

РАСЧЕТ ХАРАКТЕРИСТИК ЧЕТЫРЕХПОЛЮСНИКА В СИСТЕМЕ Z ПАРАМЕТРОВ…………………………………………………………………………….117

Классификация фильтров.Классификация по пропускаемым частотам………………………………………………………………………………..123

Классификация по схемам звеньев………………………………………...128

Разновидности ФНЧ прототипов…………………………………………….128

4. ТРЕХФАЗНЫЕ ЦЕПИ…………………………………………………………………133

ТРЕХФАЗНАЯ СИСТЕМА ЭДС………………………………………………………...133

ТРЕХФАЗНАЯ ЦЕПЬ…………………………………………………………………….135

ОСНОВНЫЕ СХЕМЫ СОЕДИНЕНИЯ ТРЕХФАЗНЫХ ЦЕПЕЙ…………………...135

РАСЧЕТ ТРЕХФАЗНЫХ ЦЕПЕЙ……………………………………………………….143

НАЗНАЧЕНИЕ ЭЛЕКТРИЧЕСКИХ МАШИН………………………………………….146

ПРЕОБРАЗОВАНИЕ ЭНЕРГИИ В ЭЛЕКТРИЧЕСКИХ МАШИНАХ……………….146

ПРИНЦИП РАБОТЫ АСИНХРОННОГО ДВИГАТЕЛЯ……………………………..147

ВРАЩАЮЩЕЕСЯ МАГНИТНОЕ ПОЛЕ……………………………………………….149

РЕЖИМ РАБОТЫ ТРЕХФАЗНОЙ АСИНХРОННОЙ МАШИНЫ…………………..152

МЕТОДЫ РЕГУЛИРОВАНИЯ ЧАСТОТЫ ВРАЩЕНИЯ АСИНХРОННЫХ ДВИГАТЕЛЕЙ……………………………………………………………………………..155

СИНХРОННЫЕ МАШИНЫ………………………………………………………………156

5. ПЕРЕХОДНЫЕ ПРОЦЕССЫ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ……158

ОБЩАЯ СХЕМА ПРИМЕНЕНИЯ КЛАССИЧЕСКОГО МЕТОДА АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ………………………………………………………….162

СОСТАВЛЕНИЕ УРАВНЕНИЙ ДЛЯ СВОБОДНЫХ ТОКОВ И НАПРЯЖЕНИЙ...164

СОСТАВЛЕНИЕ ХАРАКТЕРИСТИЧЕСКОГО УРАВНЕНИЯ СИСТЕМЫ………...166

ОПРЕДЕЛЕНИЕ ПОСТОЯННЫХ ИНТЕГРИРОВАНИЯ В КЛАССИЧЕСКОМ МЕТОДЕ……………………………………………………………………………………169

ПРИМЕРЫ РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ИЗМЕНЕНИИ ФОРМЫ ВОЗДЕЙСТВУЮЩЕГО СИГНАЛА……………………………………………………..173